 , όπου
, όπου  μια αρχική της
μια αρχική της  . H
. H  είναι παραγωγίσιμη και ορισμένη στο
είναι παραγωγίσιμη και ορισμένη στο  .
.1) Να βρεθεί το πεδίο ορισμού της

2) Nα βρεθεί η παράγωγος της

3) Aν στο
 παρουσιάζει η
παρουσιάζει η  τοπικό ακρότατο να δείξετε οτι
τοπικό ακρότατο να δείξετε οτι 
4) Υπάρχει σημείο
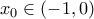 ώστε η εφαπτομένη της
ώστε η εφαπτομένη της  να είναι παράλλη προς τον
να είναι παράλλη προς τον 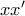 , όπως υπάρχει σημείο
, όπως υπάρχει σημείο  ώστε η εφαπτομένη της
ώστε η εφαπτομένη της  να είναι παράλλη προς τον
να είναι παράλλη προς τον 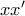 αλλά δεν είναι δυνατόν ποτέ
αλλά δεν είναι δυνατόν ποτέ  .
.

 , όπως υπάρχει σημείο
, όπως υπάρχει σημείο  και μετά έχει τοπικό ακρότατο στο
και μετά έχει τοπικό ακρότατο στο 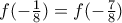
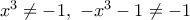 δηλαδή
δηλαδή  άρα το πεδίο ορισμού της
άρα το πεδίο ορισμού της  (…το
(…το 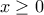 μάλλον τυπογραφικό είναι…)
μάλλον τυπογραφικό είναι…)

 ώστε
ώστε 