M.S.Vovos έγραψε:Μια απογευματινή κατασκευή.
Έστω η συνεχής και άρτια συνάρτηση

. Αν

είναι η παράγουσα της

, που διέρχεται από την αρχή των αξόνων και για κάθε

ισχύει:
 , τότε:
(α.i)
, τότε:
(α.i) Να αποδείξετε ότι η

είναι περιττή στο

.
(α.ii.) Να αποδείξετε ότι

,

.
(β) Να αποδείξετε ότι η

είναι αντιστρέψιμη στα
![(-\infty ,0] (-\infty ,0]](/forum/ext/geomar/texintegr/latexrender/pictures/f9d75a40b8eadac31117745d2255ef61.png)
και

και να βρείτε τον τύπο της

στα εν λόγω διαστήματα. Είναι η

αντιστρέψιμη στο

?
(γ) Να υπολογίσετε το εμβαδόν του χωρίου Ω, που περικλείεται από τη γραφική παράσταση της συνάρτησης

τον άξονες συντεταγμένων και την ευθεία

αν γνωρίζετε ότι:
 Φιλικά,
Φιλικά,
Μάριος
Ολίγον τι ψαρωτικό θεματάκι μέχρις να πιάσεις τη φιλοσοφία του! Κατά τα άλλα κυλάει ομαλά.
(α.ι) Εφόσον η γραφική παράσταση της

περνάει από την αρχή των αξόνων θα είναι

. Τότε επειδή η

είναι άρτια θα ισχύει ότι για κάθε

θα είναι και

καθώς και

Κατά συνέπεια θα είναι

και άρα
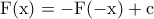
. Επειδή όμως

θα είναι εν τέλει

και άρα

οπότε η

είναι τελικά περιττή.
(α.ii) Η

ως παράγουσα της συνεχούς

είναι παραγωγίσιμη με

. Συνεπώς είναι γνήσια αύξουσα και άρα

. Η δοσμένη σχέση δίδει:
![\displaystyle{\begin{aligned}
{\rm F}\left ( f(x) \right ) + {\rm F} \left ( \ln \frac{1}{x^2+1} \right ) =0 &\Leftrightarrow {\rm F}\left ( f(x) \right ) +{\rm F}\left ( -\ln \left ( x^2+1 \right ) \right ) =0 \\
&\!\!\!\!\!\!\!\!\! \!\overset{{\rm F} \; \text{\gr περιττή}}{\Leftarrow \! =\! =\! =\! =\! \Rightarrow} {\rm F}\left ( f(x) \right )-{\rm F}\left ( \ln \left ( x^2+1 \right ) \right ) =0 \\
&\Leftrightarrow {\rm F}\left ( f(x) \right ) = {\rm F}\left ( \ln \left ( x^2+1 \right ) \right ) \\
&\!\!\!\!\overset{{\rm F} \; \; \begin{tikzpicture}
\draw [thick , >->] (0, 0) -- (0, 0.3);
\end{tikzpicture}}{ \Leftarrow \! =\! \Rightarrow} f(x) = \ln \left ( x^2+1 \right ) \quad , \quad x \in \mathbb{R}
\end{aligned}} \displaystyle{\begin{aligned}
{\rm F}\left ( f(x) \right ) + {\rm F} \left ( \ln \frac{1}{x^2+1} \right ) =0 &\Leftrightarrow {\rm F}\left ( f(x) \right ) +{\rm F}\left ( -\ln \left ( x^2+1 \right ) \right ) =0 \\
&\!\!\!\!\!\!\!\!\! \!\overset{{\rm F} \; \text{\gr περιττή}}{\Leftarrow \! =\! =\! =\! =\! \Rightarrow} {\rm F}\left ( f(x) \right )-{\rm F}\left ( \ln \left ( x^2+1 \right ) \right ) =0 \\
&\Leftrightarrow {\rm F}\left ( f(x) \right ) = {\rm F}\left ( \ln \left ( x^2+1 \right ) \right ) \\
&\!\!\!\!\overset{{\rm F} \; \; \begin{tikzpicture}
\draw [thick , >->] (0, 0) -- (0, 0.3);
\end{tikzpicture}}{ \Leftarrow \! =\! \Rightarrow} f(x) = \ln \left ( x^2+1 \right ) \quad , \quad x \in \mathbb{R}
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/02155820f4ad4fc3814cc080d75b3f1a.png) (β)
(β) Η

είναι παραγωγίσιμη στο

με παράγωγο

. Είναι

. Επίσης
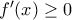
για κάθε
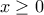
. Άρα στο

η

είναι γνήσια αύξουσα ενώ στο
![(-\infty, 0] (-\infty, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/8bb8e3006289394bd593c5b7a4904dd6.png)
η συνάρτηση

είναι γνήσια φθίνουσα. Συνεπώς σε καθένα από τα διαστήματα

και
![(-\infty, 0] (-\infty, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/8bb8e3006289394bd593c5b7a4904dd6.png)
είναι η

αντιστρέψιμη. Στο

δε μπορεί να είναι αφού

λόγω αρτιότητας.
Ας βρούμε την αντίστροφη στο

. Θέτουμε

και τότε:

Συνεπώς η αντίστροφη στο

ο τύπος της αντίστροφης είναι ο

.
(γ) Το εμβαδόν του χωρίου

που περικλείεται της γραφικής παράστασης , των αξόνων και της ευθείας

δίδεται του τύπου

Όμως

για κάθε

αφού

και κατά συνέπεια

. Άρα:
![\displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{-1}^{0} f(x) \, {\rm d}x \\
&= \int_{-1}^{0} \ln \left ( x^2+1 \right ) \, {\rm d}x\\
&=\int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x \\
&= \left [ x \ln \left ( x^2+1 \right ) \right ]_0^1 - 2\int_{0}^{1} \frac{x^2}{x^2+1} \, {\rm d}x \\
&= \ln 2 - 2 \int_{0}^{1} \frac{x^2+1-1}{x^2+1} \, {\rm d}x\\
&= \ln 2 - 2 \int_{0}^{1} \left ( 1 - \frac{1}{x^2+1} \right ) \, {\rm d}x \\
&= \ln 2 - 2 + 2 \int_{0}^{1} \frac{{\rm d}x}{x^2+1} \\
&= \ln 2 - 2 + \frac{2 \pi}{4} \\
&= \ln 2 - 2 + \frac{\pi}{2} \approx 0.26394
\end{aligned}} \displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{-1}^{0} f(x) \, {\rm d}x \\
&= \int_{-1}^{0} \ln \left ( x^2+1 \right ) \, {\rm d}x\\
&=\int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x \\
&= \left [ x \ln \left ( x^2+1 \right ) \right ]_0^1 - 2\int_{0}^{1} \frac{x^2}{x^2+1} \, {\rm d}x \\
&= \ln 2 - 2 \int_{0}^{1} \frac{x^2+1-1}{x^2+1} \, {\rm d}x\\
&= \ln 2 - 2 \int_{0}^{1} \left ( 1 - \frac{1}{x^2+1} \right ) \, {\rm d}x \\
&= \ln 2 - 2 + 2 \int_{0}^{1} \frac{{\rm d}x}{x^2+1} \\
&= \ln 2 - 2 + \frac{2 \pi}{4} \\
&= \ln 2 - 2 + \frac{\pi}{2} \approx 0.26394
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/717af3716de966ec78823fa8f15a1a58.png)

Για τον υπολογισμό του ολοκληρώματος

θέτουμε
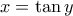
και καταλήγουμε στο

που βγαλα πάνω.
Υ.Σ: Το ολοκλήρωμα που δίδεται πάνω δε μπόρεσα να το χρησιμοποιήσω ... οπότε αναγκάστηκα να αλλάξω γραμμή πλεύσης.
 . Αν
. Αν  είναι η παράγουσα της
είναι η παράγουσα της  , που διέρχεται από την αρχή των αξόνων και για κάθε
, που διέρχεται από την αρχή των αξόνων και για κάθε  ισχύει:
ισχύει: , τότε:
(α.i) Να αποδείξετε ότι η
, τότε:
(α.i) Να αποδείξετε ότι η  είναι περιττή στο
είναι περιττή στο  .
. ,
,  .
. είναι αντιστρέψιμη στα
είναι αντιστρέψιμη στα ![(-\infty ,0] (-\infty ,0]](/forum/ext/geomar/texintegr/latexrender/pictures/f9d75a40b8eadac31117745d2255ef61.png) και
και  και να βρείτε τον τύπο της
και να βρείτε τον τύπο της  στα εν λόγω διαστήματα. Είναι η
στα εν λόγω διαστήματα. Είναι η  αντιστρέψιμη στο
αντιστρέψιμη στο  ?
? τον άξονες συντεταγμένων και την ευθεία
τον άξονες συντεταγμένων και την ευθεία  αν γνωρίζετε ότι:
αν γνωρίζετε ότι: Φιλικά,
Φιλικά,
 περνάει από την αρχή των αξόνων θα είναι
περνάει από την αρχή των αξόνων θα είναι  . Τότε επειδή η
. Τότε επειδή η  θα είναι και
θα είναι και  καθώς και
καθώς και 
 και άρα
και άρα 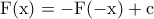 . Επειδή όμως
. Επειδή όμως  και άρα
και άρα  οπότε η
οπότε η  . Συνεπώς είναι γνήσια αύξουσα και άρα
. Συνεπώς είναι γνήσια αύξουσα και άρα  . Η δοσμένη σχέση δίδει:
. Η δοσμένη σχέση δίδει:![\displaystyle{\begin{aligned}
{\rm F}\left ( f(x) \right ) + {\rm F} \left ( \ln \frac{1}{x^2+1} \right ) =0 &\Leftrightarrow {\rm F}\left ( f(x) \right ) +{\rm F}\left ( -\ln \left ( x^2+1 \right ) \right ) =0 \\
&\!\!\!\!\!\!\!\!\! \!\overset{{\rm F} \; \text{\gr περιττή}}{\Leftarrow \! =\! =\! =\! =\! \Rightarrow} {\rm F}\left ( f(x) \right )-{\rm F}\left ( \ln \left ( x^2+1 \right ) \right ) =0 \\
&\Leftrightarrow {\rm F}\left ( f(x) \right ) = {\rm F}\left ( \ln \left ( x^2+1 \right ) \right ) \\
&\!\!\!\!\overset{{\rm F} \; \; \begin{tikzpicture}
\draw [thick , >->] (0, 0) -- (0, 0.3);
\end{tikzpicture}}{ \Leftarrow \! =\! \Rightarrow} f(x) = \ln \left ( x^2+1 \right ) \quad , \quad x \in \mathbb{R}
\end{aligned}} \displaystyle{\begin{aligned}
{\rm F}\left ( f(x) \right ) + {\rm F} \left ( \ln \frac{1}{x^2+1} \right ) =0 &\Leftrightarrow {\rm F}\left ( f(x) \right ) +{\rm F}\left ( -\ln \left ( x^2+1 \right ) \right ) =0 \\
&\!\!\!\!\!\!\!\!\! \!\overset{{\rm F} \; \text{\gr περιττή}}{\Leftarrow \! =\! =\! =\! =\! \Rightarrow} {\rm F}\left ( f(x) \right )-{\rm F}\left ( \ln \left ( x^2+1 \right ) \right ) =0 \\
&\Leftrightarrow {\rm F}\left ( f(x) \right ) = {\rm F}\left ( \ln \left ( x^2+1 \right ) \right ) \\
&\!\!\!\!\overset{{\rm F} \; \; \begin{tikzpicture}
\draw [thick , >->] (0, 0) -- (0, 0.3);
\end{tikzpicture}}{ \Leftarrow \! =\! \Rightarrow} f(x) = \ln \left ( x^2+1 \right ) \quad , \quad x \in \mathbb{R}
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/02155820f4ad4fc3814cc080d75b3f1a.png)
 . Είναι
. Είναι  . Επίσης
. Επίσης 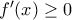 για κάθε
για κάθε 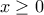 . Άρα στο
. Άρα στο  η
η ![(-\infty, 0] (-\infty, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/8bb8e3006289394bd593c5b7a4904dd6.png) η συνάρτηση
η συνάρτηση  λόγω αρτιότητας.
λόγω αρτιότητας.  και τότε:
και τότε:
 .
. που περικλείεται της γραφικής παράστασης , των αξόνων και της ευθείας
που περικλείεται της γραφικής παράστασης , των αξόνων και της ευθείας 
 για κάθε
για κάθε  και κατά συνέπεια
και κατά συνέπεια  . Άρα:
. Άρα:![\displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{-1}^{0} f(x) \, {\rm d}x \\
&= \int_{-1}^{0} \ln \left ( x^2+1 \right ) \, {\rm d}x\\
&=\int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x \\
&= \left [ x \ln \left ( x^2+1 \right ) \right ]_0^1 - 2\int_{0}^{1} \frac{x^2}{x^2+1} \, {\rm d}x \\
&= \ln 2 - 2 \int_{0}^{1} \frac{x^2+1-1}{x^2+1} \, {\rm d}x\\
&= \ln 2 - 2 \int_{0}^{1} \left ( 1 - \frac{1}{x^2+1} \right ) \, {\rm d}x \\
&= \ln 2 - 2 + 2 \int_{0}^{1} \frac{{\rm d}x}{x^2+1} \\
&= \ln 2 - 2 + \frac{2 \pi}{4} \\
&= \ln 2 - 2 + \frac{\pi}{2} \approx 0.26394
\end{aligned}} \displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{-1}^{0} f(x) \, {\rm d}x \\
&= \int_{-1}^{0} \ln \left ( x^2+1 \right ) \, {\rm d}x\\
&=\int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x \\
&= \left [ x \ln \left ( x^2+1 \right ) \right ]_0^1 - 2\int_{0}^{1} \frac{x^2}{x^2+1} \, {\rm d}x \\
&= \ln 2 - 2 \int_{0}^{1} \frac{x^2+1-1}{x^2+1} \, {\rm d}x\\
&= \ln 2 - 2 \int_{0}^{1} \left ( 1 - \frac{1}{x^2+1} \right ) \, {\rm d}x \\
&= \ln 2 - 2 + 2 \int_{0}^{1} \frac{{\rm d}x}{x^2+1} \\
&= \ln 2 - 2 + \frac{2 \pi}{4} \\
&= \ln 2 - 2 + \frac{\pi}{2} \approx 0.26394
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/717af3716de966ec78823fa8f15a1a58.png)
 Για τον υπολογισμό του ολοκληρώματος
Για τον υπολογισμό του ολοκληρώματος  θέτουμε
θέτουμε 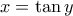 και καταλήγουμε στο
και καταλήγουμε στο  που βγαλα πάνω.
που βγαλα πάνω.
 , κάνεις την αντικατάσταση
, κάνεις την αντικατάσταση , βρίσκεις
, βρίσκεις
 συνεχής με συνεχή παράγωγο στο
συνεχής με συνεχή παράγωγο στο ![\displaystyle{\left[ {\alpha ,\beta } \right]} \displaystyle{\left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/732d2d8cc68c4c7a5e1630eb99f15d40.png) . αν η
. αν η ![\displaystyle{\int\limits_\alpha ^\beta {f\left( x \right)} \,dx + \int\limits_{f\left( \alpha \right)}^{f\left( \beta \right)} {{f^{ - 1}}\left( x \right)} \,dx = \left[ {xf\left( x \right)} \right]_\alpha ^\beta } \displaystyle{\int\limits_\alpha ^\beta {f\left( x \right)} \,dx + \int\limits_{f\left( \alpha \right)}^{f\left( \beta \right)} {{f^{ - 1}}\left( x \right)} \,dx = \left[ {xf\left( x \right)} \right]_\alpha ^\beta }](/forum/ext/geomar/texintegr/latexrender/pictures/29df0096161f1cc579cb4416cb9011fa.png)
![\displaystyle{\int\limits_0^1 {\ln \left( {{x^2} + 1} \right)} \,dx + \int\limits_0^{\ln 2} {\sqrt {{e^x} - 1} } dx = \left[ {x\ln \left( {{x^2} + 1} \right)} \right]_0^1} \displaystyle{\int\limits_0^1 {\ln \left( {{x^2} + 1} \right)} \,dx + \int\limits_0^{\ln 2} {\sqrt {{e^x} - 1} } dx = \left[ {x\ln \left( {{x^2} + 1} \right)} \right]_0^1}](/forum/ext/geomar/texintegr/latexrender/pictures/7843b832ce8084e3f69414475af244a6.png)