...Συνεχίζοντας για το 3) σκέφτομαι τα εξής :
Έχει αποδειχθεί από το 1) ότι η

παρουσιάζει στα σημεία :

ολικό ελάχιστο το

.
Γνωρίζουμε ότι η

είναι συνεχής στο
![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png)
.
Επομένως από το θεώρημα Μεγίστης- Ελαχίστης Τιμής συμπεραίνουμε ότι η μη σταθερή

παρουσιάζει μέγιστη τιμή στο
![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png)
.
Έστω ότι υπάρχουν δύο τιμές

στις οποίες η

παρουσιάζει μέγιστο.
Τότε πάλι από το θεώρημα Μεγίστης- Ελαχίστης Τιμής συμπεραίνουμε ότι η μη σταθερή

παρουσιάζει ελάχιστη τιμή στο
![[p_{1} , p_{2}] [p_{1} , p_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/29e8c6b9b152b2577fb7897048a4faca.png)
. Άτοπο, διότι μεταξύ των

δεν υπάρχει άλλο ελάχιστο.
Ομοίως αποδεικνύεται ότι και μεταξύ των

υπάρχει ακριβώς ένα μέγιστο.
Άρα αποδείξαμε ότι η

παρουσιάζει ακριβώς δύο τοπικά μέγιστα στα

. Το ένα στο διάστημα
![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png)
και το άλλο στο
![[2,3] [2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/d5138fec13c27bb6c645b29cdfa97a84.png)
.
4) Εφαρμόζοντας τέσσερεις φορές Θεώρημα Rolle στα διαστήματα :
![[1,x_{1}], [x_{1},2] , [2,x_{2}] , [x_{2},3] [1,x_{1}], [x_{1},2] , [2,x_{2}] , [x_{2},3]](/forum/ext/geomar/texintegr/latexrender/pictures/af4fadd989f7d58f6393cc7fc7c22296.png)
για την συνάρτηση

προκύπτει το ζητούμενο.
Με συγχωρείτε ... ξέχασα!
Το Rolle εφαρμόζεται διότι από το Θεώρημα Fermat ισχύει :

Φιλικά
Σταμ. Γλάρος


 παίρνει ολικό ελάχιστο
παίρνει ολικό ελάχιστο είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
![(-\infty ,1] (-\infty ,1]](/forum/ext/geomar/texintegr/latexrender/pictures/13827b029cca637036505ae5473cdd6e.png)
 έχει ακριβώς δύο τοπικά μέγιστα.
έχει ακριβώς δύο τοπικά μέγιστα. έχει ακριβώς τέσσερεις ρίζες
έχει ακριβώς τέσσερεις ρίζες να δείξετε ότι η εξίσωση
να δείξετε ότι η εξίσωση 

 έχει το πολύ
έχει το πολύ  ρίζες.
ρίζες.
 και το τριώνυμο έχει τις ρίζες
και το τριώνυμο έχει τις ρίζες  οπότε η διάταξη των ριζών της παραγώγου είναι
οπότε η διάταξη των ριζών της παραγώγου είναι  και το πρόσημο είναι εναλλάξ
και το πρόσημο είναι εναλλάξ  ξεκινώντας από το τέρμα δεξία διάστημα
ξεκινώντας από το τέρμα δεξία διάστημα 
 είναι πολυώνυμο 4ου βαθμού και έχει τουλάχιστον τέσσερις ρίζες (αφού το
είναι πολυώνυμο 4ου βαθμού και έχει τουλάχιστον τέσσερις ρίζες (αφού το  έχει πέντε ρίζες). Άρα έχει ακριβώς τέσσερις ρίζες.
έχει πέντε ρίζες). Άρα έχει ακριβώς τέσσερις ρίζες. η εξίσωση σε κάθε 'ένα διάστημα έχει ακριβώς μια ρίζα, άρα συνολικά ακριβώς έξι.
η εξίσωση σε κάθε 'ένα διάστημα έχει ακριβώς μια ρίζα, άρα συνολικά ακριβώς έξι. (που είναι επίσης άμεση) στο
(που είναι επίσης άμεση) στο ![\displaystyle{[1,2].} \displaystyle{[1,2].}](/forum/ext/geomar/texintegr/latexrender/pictures/1abe7959b3ee54339e518ff19df3c2cc.png)
 με
με 


 (1)
(1)
 (2)
(2)
 (3)
(3) .
. .
.


 (4)
(4)
 (5)
(5)
 (6)
(6) .
.![( - \infty ,1 ] ( - \infty ,1 ]](/forum/ext/geomar/texintegr/latexrender/pictures/81ede3a8e79296b37c7d99a273feb9b3.png) .
. ολικό ελάχιστο το
ολικό ελάχιστο το  .
.![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) .
. στις οποίες η
στις οποίες η ![[p_{1} , p_{2}] [p_{1} , p_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/29e8c6b9b152b2577fb7897048a4faca.png) . Άτοπο, διότι μεταξύ των
. Άτοπο, διότι μεταξύ των  δεν υπάρχει άλλο ελάχιστο.
δεν υπάρχει άλλο ελάχιστο. υπάρχει ακριβώς ένα μέγιστο.
υπάρχει ακριβώς ένα μέγιστο. . Το ένα στο διάστημα
. Το ένα στο διάστημα ![[2,3] [2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/d5138fec13c27bb6c645b29cdfa97a84.png) .
.![[1,x_{1}], [x_{1},2] , [2,x_{2}] , [x_{2},3] [1,x_{1}], [x_{1},2] , [2,x_{2}] , [x_{2},3]](/forum/ext/geomar/texintegr/latexrender/pictures/af4fadd989f7d58f6393cc7fc7c22296.png) για την συνάρτηση
για την συνάρτηση  προκύπτει το ζητούμενο.
προκύπτει το ζητούμενο.
![[1,2],[2,3] [1,2],[2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/d8a529ece1002744c91834b40d9637bf.png)
 έχει το πολύ
έχει το πολύ  ρίζες και σίγουρα
ρίζες και σίγουρα ![\left [ (x-1)(x-2)(x-3)-\sqrt{a} \right ]\left [ (x-1)(x-2)(x-3)+\sqrt{a} \right ]=0 \left [ (x-1)(x-2)(x-3)-\sqrt{a} \right ]\left [ (x-1)(x-2)(x-3)+\sqrt{a} \right ]=0](/forum/ext/geomar/texintegr/latexrender/pictures/817ff055e15f69dd128e593f0768f58b.png)
 στις τιμές
στις τιμές  και
και  αντίστοιχα επομένως έχει δυο ρίζες και μια τρεις.Ο δεύτερος παράγοντας έχει πρόσημο
αντίστοιχα επομένως έχει δυο ρίζες και μια τρεις.Ο δεύτερος παράγοντας έχει πρόσημο 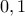 και
και  αντιστοίχως. Άρα έχουμε άλλες τρεις.
αντιστοίχως. Άρα έχουμε άλλες τρεις. να είναι
να είναι 


 ρίζες.
ρίζες.