(α) Αν θεωρήσουμε δεδομένο το όριο
![\displaystyle{\log x = \lim \limits_{n \rightarrow +\infty} n \left( \sqrt[n]{a} -1 \right)} \displaystyle{\log x = \lim \limits_{n \rightarrow +\infty} n \left( \sqrt[n]{a} -1 \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/1a58d1549a8038b31a2b0c35fb32a6db.png)
το οποίο έχουμε δει
εδώ τότε το συμπέρασμα έπεται άμεσα. Συνεπώς
![\displaystyle{\lim_{ n \rightarrow +\infty} n \left( \sqrt[n]{x^2+1} - 1 \right) = \log \left( x^2+ 1 \right)} \displaystyle{\lim_{ n \rightarrow +\infty} n \left( \sqrt[n]{x^2+1} - 1 \right) = \log \left( x^2+ 1 \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/ee50dec9c7295858a3c26a183bf8f82c.png)
(β) Οι εφαπτομένες της γραφικής παράστασης της

που άγονται από το σημείο

είναι της μορφής
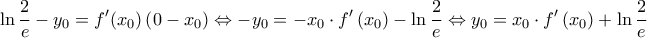
Όμως το σημείο

και οπότε

. Οπότε καλούμαστε να λύσουμε την εξίσωση

Παραλλείπω τις πράξεις ( όποιος θέλει να τις συμπληρώσει be my guest ) αλλά από πάνω βγάζουμε

. Άρα οι εφαπτομένες είναι οι ευθείες

και

.
(γ) Επειδή η

είναι κυρτή αυτό σημαίνει ότι η εφαπτομένη θα είναι κάτω από τη γραφική παράσταση της

με εξαίρεση το σημείο επαφής. Άρα το ζητούμενο εμβαδόν είναι ίσο με:
![\displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{0}^{1} \left ( f(x) - x + \ln \frac{2}{e} \right ) \, {\rm d}x\\
&= \int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x - \int_{0}^{1}\left ( x - \ln \frac{2}{e} \right ) \, {\rm d}x\\
&= \int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x - \frac{3}{2} + \log 2 \\
&=\left [ x\log \left ( x^2+1 \right ) \right ]_0^1 - 2\int_{0}^{1} \frac{x^2}{x^2+1} \, {\rm d}x - \frac{3}{2} + \log 2\\
&= \log 2 - 2 \int_{0}^{1} \frac{x^2+1-1}{x^2+1} \, {\rm d}x - \frac{3}{2} + \log 2 \\
&= \log 2 - 2\int_{0}^{1} \left ( 1 - \frac{1}{x^2+1}\right ) \, {\rm d}x - \frac{3}{2} + \log 2 \\
&= \log 2 - 2 + \frac{\pi}{2} - \frac{3}{4} + \log 2 \\
&= \frac{\pi}{2} + 2 \log 2 - \frac{11}{4} \\
&\sim 0.20709
\end{aligned}} \displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{0}^{1} \left ( f(x) - x + \ln \frac{2}{e} \right ) \, {\rm d}x\\
&= \int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x - \int_{0}^{1}\left ( x - \ln \frac{2}{e} \right ) \, {\rm d}x\\
&= \int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x - \frac{3}{2} + \log 2 \\
&=\left [ x\log \left ( x^2+1 \right ) \right ]_0^1 - 2\int_{0}^{1} \frac{x^2}{x^2+1} \, {\rm d}x - \frac{3}{2} + \log 2\\
&= \log 2 - 2 \int_{0}^{1} \frac{x^2+1-1}{x^2+1} \, {\rm d}x - \frac{3}{2} + \log 2 \\
&= \log 2 - 2\int_{0}^{1} \left ( 1 - \frac{1}{x^2+1}\right ) \, {\rm d}x - \frac{3}{2} + \log 2 \\
&= \log 2 - 2 + \frac{\pi}{2} - \frac{3}{4} + \log 2 \\
&= \frac{\pi}{2} + 2 \log 2 - \frac{11}{4} \\
&\sim 0.20709
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/caf3c7d6fa1e260729ebfac593de3d3b.png) Σημείωση:
Σημείωση: Το πρώτο ερώτημα το θεωρώ εκτός πνεύματος εξετάσεων αφού το όριο ακολουθίας ( και τι ακολουθίας εδώ ) γενικά δεν εξετάζεται παρόλο που εψιλοντός ορισμός είναι τυπικά μέσα στην ύλη. .... !! Δε θα θελα να δω κάτι τέτοιο στις εξετάσεις.
 και η ακολουθία
και η ακολουθία  με τύπο
με τύπο ![\displaystyle \mathrm{a_{n}=n\left ( \sqrt[\mathrm{n}]{\mathrm{x^{2}+1}}-1 \right )} \displaystyle \mathrm{a_{n}=n\left ( \sqrt[\mathrm{n}]{\mathrm{x^{2}+1}}-1 \right )}](/forum/ext/geomar/texintegr/latexrender/pictures/d84d20c2a7da44be0dcd93120403a566.png) ,
,  . Ορίζουμε τη συνάρτηση
. Ορίζουμε τη συνάρτηση  τέτοια ώστε:
τέτοια ώστε:
 ,
,  .
. που άγονται από το σημείο
που άγονται από το σημείο  .
. , τον άξονα
, τον άξονα  και την ευθεία
και την ευθεία  , αν γνωρίζετε ότι
, αν γνωρίζετε ότι  .
.
![\displaystyle{\log x = \lim \limits_{n \rightarrow +\infty} n \left( \sqrt[n]{a} -1 \right)} \displaystyle{\log x = \lim \limits_{n \rightarrow +\infty} n \left( \sqrt[n]{a} -1 \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/1a58d1549a8038b31a2b0c35fb32a6db.png) το οποίο έχουμε δει
το οποίο έχουμε δει ![\displaystyle{\lim_{ n \rightarrow +\infty} n \left( \sqrt[n]{x^2+1} - 1 \right) = \log \left( x^2+ 1 \right)} \displaystyle{\lim_{ n \rightarrow +\infty} n \left( \sqrt[n]{x^2+1} - 1 \right) = \log \left( x^2+ 1 \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/ee50dec9c7295858a3c26a183bf8f82c.png)
 που άγονται από το σημείο
που άγονται από το σημείο  είναι της μορφής
είναι της μορφής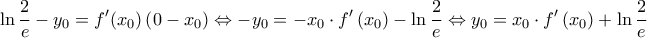
 και οπότε
και οπότε  . Οπότε καλούμαστε να λύσουμε την εξίσωση
. Οπότε καλούμαστε να λύσουμε την εξίσωση
 . Άρα οι εφαπτομένες είναι οι ευθείες
. Άρα οι εφαπτομένες είναι οι ευθείες  και
και  .
.![\displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{0}^{1} \left ( f(x) - x + \ln \frac{2}{e} \right ) \, {\rm d}x\\
&= \int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x - \int_{0}^{1}\left ( x - \ln \frac{2}{e} \right ) \, {\rm d}x\\
&= \int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x - \frac{3}{2} + \log 2 \\
&=\left [ x\log \left ( x^2+1 \right ) \right ]_0^1 - 2\int_{0}^{1} \frac{x^2}{x^2+1} \, {\rm d}x - \frac{3}{2} + \log 2\\
&= \log 2 - 2 \int_{0}^{1} \frac{x^2+1-1}{x^2+1} \, {\rm d}x - \frac{3}{2} + \log 2 \\
&= \log 2 - 2\int_{0}^{1} \left ( 1 - \frac{1}{x^2+1}\right ) \, {\rm d}x - \frac{3}{2} + \log 2 \\
&= \log 2 - 2 + \frac{\pi}{2} - \frac{3}{4} + \log 2 \\
&= \frac{\pi}{2} + 2 \log 2 - \frac{11}{4} \\
&\sim 0.20709
\end{aligned}} \displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{0}^{1} \left ( f(x) - x + \ln \frac{2}{e} \right ) \, {\rm d}x\\
&= \int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x - \int_{0}^{1}\left ( x - \ln \frac{2}{e} \right ) \, {\rm d}x\\
&= \int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x - \frac{3}{2} + \log 2 \\
&=\left [ x\log \left ( x^2+1 \right ) \right ]_0^1 - 2\int_{0}^{1} \frac{x^2}{x^2+1} \, {\rm d}x - \frac{3}{2} + \log 2\\
&= \log 2 - 2 \int_{0}^{1} \frac{x^2+1-1}{x^2+1} \, {\rm d}x - \frac{3}{2} + \log 2 \\
&= \log 2 - 2\int_{0}^{1} \left ( 1 - \frac{1}{x^2+1}\right ) \, {\rm d}x - \frac{3}{2} + \log 2 \\
&= \log 2 - 2 + \frac{\pi}{2} - \frac{3}{4} + \log 2 \\
&= \frac{\pi}{2} + 2 \log 2 - \frac{11}{4} \\
&\sim 0.20709
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/caf3c7d6fa1e260729ebfac593de3d3b.png)
