ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε: ↑Τετ Μαρ 06, 2019 9:25 pm
KAKABASBASILEIOS έγραψε: ↑Τετ Μαρ 06, 2019 2:18 am
...συνεχίζοντας το κάψιμο μια αποψινή έμπνευση...
Δίνεται συνάρτηση

για την οποία ισχύει ότι

για κάθε

.
Αν γνωρίζουμε ότι είναι γνήσια φθίνουσα στο διάστημα

τότε:
Α. Να δειχτεί ότι η

είναι συνεχής στο

Β. Αν επιπλέον γνωρίζουμε ότι η συνάρτηση

είναι ορισμένη και παραγωγίσιμη στο

με

να δείξετε ότι η συνάρτηση

είναι παραγωγίσιμη και να βρεθεί ο τύπος της.
Φιλικά και Μαθηματικά
Βασίλης
Καλησπέρα σας. Πολύ ωραίο θέμα!
Για το Α προς το παρόν (ελπίζω σωστά).
Έστω τυχαίο

που ανήκει στο

. Τότε:

άρα

Ακόμη

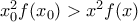

Συνεπώς

και από το κριτήριο παρεμβολής προκύπτει

άρα η

είναι συνεχής στο

.
Αυτό που απέδειξες Χάρη είναι ότι

με όμοιο τρόπο αποδεικνύεται ότι

που μαζί με το προηγούμενο δίνει την συνέχεια.
Το Β είναι σχεδόν τετριμμένο.
Από την υπόθεση έχουμε ότι

Αρα

(1)
Είναι εύκολο να δούμε ότι η

είναι

.
Για

η συναρτησιακή δίνει ότι

δηλαδή

Ετσι η (1) δίνει

.
Αρα

δηλαδή

που προφανώς είναι παραγωγίσημη.
Η γνώμη μου είναι ότι η άσκηση είναι εντελώς ακατάλληλη για την πλειονότητα
των μαθητών της Γ Λυκείου.
Για να το δικαιολογήσω αρκεί να πω ότι αρέσει στον Χάρη ,καθώς και τέτοιου τύπου ασκήσεις
δεν βρίσκονται σε σοβαρά βιβλία Απειροστικού.
π.χ Νεγρεπόντης ,Γιαννόπουλος ,Spivak.
 για την οποία ισχύει ότι
για την οποία ισχύει ότι  για κάθε
για κάθε  .
.  τότε:
τότε:  είναι συνεχής στο
είναι συνεχής στο 
 είναι ορισμένη και παραγωγίσιμη στο
είναι ορισμένη και παραγωγίσιμη στο  με
με 
 είναι παραγωγίσιμη και να βρεθεί ο τύπος της.
είναι παραγωγίσιμη και να βρεθεί ο τύπος της. 
 που ανήκει στο
που ανήκει στο  . Τότε:
. Τότε: άρα
άρα 

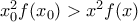

 και από το κριτήριο παρεμβολής προκύπτει
και από το κριτήριο παρεμβολής προκύπτει  άρα η
άρα η 


 (1)
(1) .
. η συναρτησιακή δίνει ότι
η συναρτησιακή δίνει ότι 

 .
.
