Al.Koutsouridis έγραψε: ↑Παρ Απρ 19, 2019 10:46 am
Με αφορμή το πρόβλημα
εδώ...
Για θετικά

ορίζουμε τον λογαριθμικό μέσο

, τον αριθμητικό μέσο

και το γεωμετρικό μέσο

.
i) Μελετήστε ως προς την μονοτονία την συνάρτηση

.
ii) Να αποδείξετε, ότι

iii) Να αποδείξετε, ότι

iv) Προσπαθήστε να κατασκευάσετε και άλλες παρόμοιες ανισότητες.
Ας δούμε το τελευταίο ερώτημα που νομίζω έχει χωριστό ενδιαφέρον.
Α) Αφού ο λογαριθμικός μέσος είναι μεταξύ του γεωμετρικού μέσου και του αριθμητικού μέσου είναι κυρτός γραμμικός συνδυασμός τους. Στην ουσία αναζήτηση ανισοτήτων σαν την ii) σημαίνει να αναζητηθούν μέσοι του μέσου γεωμετρικού και του μέσου αριθμητικού που υπερβαίνουν τον λογαριθμικό μέσο και έχουν βάρη θετικούς ακεραίους.
Ισοδύναμα αναζητούνται ρητοί

του διαστήματος

ώστε

για κάθε επιλογή των

.
Υποθέτουμε χωρίς βλάβη της γενικότητας ότι
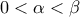
και για να απλουστεύουμε τις πράξεις ότι

με

.
Τότε

και η

ισχοδυναμεί με την

δηλαδή την

που θέλουμε να ισχύει για όλα τα

Θεωρούμε την συνάρτηση

ορισμένη στο

ώστε

για


και

. Εύκολα βγαίνει ότι η συνάρτηση αυτή είναι συνεχής. Επίσης

που σημαίνει ότι η

είναι και παραγωγίσιμη και ενδέχεται στο

να παρουσιάζει ακρότατο. Πράγματι θα δείξουμε ότι στο

παρουσιάζει μέγιστο και συγκεκριμένα ότι

για

,

.
Αρκεί να δείξουμε ότι η συνάρτηση
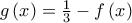
είναι θετική στα

,

.
Είναι

για

,

και

.
Πράγματι μελετώντας την

βρίσκουμε ότι είναι θετική για

και αρνητική για

και το συμπέρασμα για την

έπεται.
Οπότε πράγματι η μέγιστη τιμή είναι το

. Επομένως αφού για

είναι πάντα

αν οι υπολογισμοί μου είναι σωστοί, συμπεραίνουμε ότι αρκεί να πάρουμε

. Σημειωτέον ότι η τιμή

μας δίνει την αισότητα ii).
Β) Για την iii) εργαζόμαστε ανάλογα αν οι πράξεις είναι πιο κοπιατικές. Θέλουμε

. πάλι θέτοντας

βρίσκουμε ότι πρέπει

'Οπως πριν βρίσκουμε ότι το

είναι ένα πιθανό μέγιστο της συνάρτησης
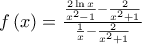
για

,

και

.
Εδώ

και ύστερα από μελέτη του αριθμητή

βρίσκουμε ότι είναι θετικός πάνω από το

και αρνητικός στο

. Επομένως κάθε επιλογή

μας δίνει μια ανισότητα σαν την iii). H iii) προκύπτει για
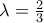
.
 ορίζουμε τον λογαριθμικό μέσο
ορίζουμε τον λογαριθμικό μέσο  , τον αριθμητικό μέσο
, τον αριθμητικό μέσο  και το γεωμετρικό μέσο
και το γεωμετρικό μέσο  .
. .
.


 του διαστήματος
του διαστήματος  ώστε
ώστε  για κάθε επιλογή των
για κάθε επιλογή των  .
.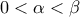 και για να απλουστεύουμε τις πράξεις ότι
και για να απλουστεύουμε τις πράξεις ότι  με
με  .
.  και η
και η  ισχοδυναμεί με την
ισχοδυναμεί με την 

 ορισμένη στο
ορισμένη στο  για
για 
 και
και  . Εύκολα βγαίνει ότι η συνάρτηση αυτή είναι συνεχής. Επίσης
. Εύκολα βγαίνει ότι η συνάρτηση αυτή είναι συνεχής. Επίσης  που σημαίνει ότι η
που σημαίνει ότι η  να παρουσιάζει ακρότατο. Πράγματι θα δείξουμε ότι στο
να παρουσιάζει ακρότατο. Πράγματι θα δείξουμε ότι στο  για
για 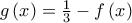 είναι θετική στα
είναι θετική στα  για
για  .
.
 και το συμπέρασμα για την
και το συμπέρασμα για την  έπεται.
έπεται.  . Επομένως αφού για
. Επομένως αφού για  αν οι υπολογισμοί μου είναι σωστοί, συμπεραίνουμε ότι αρκεί να πάρουμε
αν οι υπολογισμοί μου είναι σωστοί, συμπεραίνουμε ότι αρκεί να πάρουμε  . Σημειωτέον ότι η τιμή
. Σημειωτέον ότι η τιμή  μας δίνει την αισότητα ii).
μας δίνει την αισότητα ii). . πάλι θέτοντας
. πάλι θέτοντας 
 είναι ένα πιθανό μέγιστο της συνάρτησης
είναι ένα πιθανό μέγιστο της συνάρτησης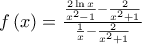 για
για  .
.

 μας δίνει μια ανισότητα σαν την iii). H iii) προκύπτει για
μας δίνει μια ανισότητα σαν την iii). H iii) προκύπτει για 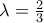 .
.