Σφαίρα και κύβος, επιφάνεια και όγκος
Συντονιστής: Μπάμπης Στεργίου
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3344
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Σφαίρα και κύβος, επιφάνεια και όγκος
Με αφορμή πρόσφατη συζήτηση εδώ, να δειχθεί ότι
Αν η συνολική επιφάνεια σφαίρας και κύβου είναι σταθερή, τότε ο συνολικός τους όγκος ελαχιστοποιείται όταν η ακμή του κύβου ισούται προς την διάμετρο της σφαίρας.
Αν η συνολική επιφάνεια σφαίρας και κύβου είναι σταθερή, τότε ο συνολικός τους όγκος ελαχιστοποιείται όταν η ακμή του κύβου ισούται προς την διάμετρο της σφαίρας.
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Λέξεις Κλειδιά:
Re: Σφαίρα και κύβος, επιφάνεια και όγκος
Γιώργο καλησπέρα...
Ωραίο το πρόβλημά σου...
Εργαζόμαστε στο ακόλουθο σχήμα:
Θεωρούμε
 την ακτίνα του κύκλου,
την ακτίνα του κύκλου,  την ακμή του κύβου και
την ακμή του κύβου και  η σταθερά τιμή του αθροίσματος των εμβαδών αυτών
η σταθερά τιμή του αθροίσματος των εμβαδών αυτώντων στερεών, η οποία βέβαια είναι τέτοια ώστε όλα τα εμφανιζόμενα ριζικά να έχουν πραγματικό νόημα.
Τότε θα είναι:

Τότε το άθροισμα των όγκων των δύο αυτών στερεών είναι:
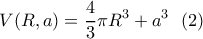
Ζητούμε επομένως την ελαχίστη τιμή της
 .
. Από την (1) έχουμε:

Άρα η (2) δίνει:

Η παράγωγος της συνάρτησης αυτής μετά από πράξεις τελικά είναι:

Η μελέτη του προσήμου της παραγώγου αυτής επειδή ο πρώτος παράγοντας είναι πάντα θετικός θα εξαρτάται από το πρόσημο του
τριωνύμου:

το οποίο μηδενίζεται για
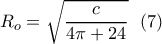
και η τιμή αυτή δίνει ασφαλώς την ελαχίστη τιμή για τη συνάρτηση
 .
.Για την τιμή αυτή η ακμή του κύβου θα είναι:
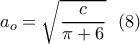
Από τις (7) και (8) εύκολα δείχνεται:

το οποίο είναι και το ζητούμενο.
Παρατήρηση:
Αναρτώ κι ένα δυναμικό σχήμα, καθότι το πρόβλημα έχει κινητικότητα.
Κώστας Δόρτσιος
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3344
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Σφαίρα και κύβος, επιφάνεια και όγκος
Καλημέρα Κώστα,
σ' ευχαριστούμε για την ενασχόληση και το δυναμικό σχήμα, παραθέτω κι εγώ μια δική μου οπτική:
Γνωρίζοντας το υπέροχο αυτό αποτέλεσμα (άμεση γενίκευση σχολικού προβλήματος), ας κινηθούμε λίγο διαφορετικά, θέτοντας (συνολική επιφάνεια σφαίρας και κύβου) και εκφράζοντας τον συνολικό όγκο σφαίρας και κύβου ως συνάρτηση της διαμέτρου της σφαίρας,
(συνολική επιφάνεια σφαίρας και κύβου) και εκφράζοντας τον συνολικό όγκο σφαίρας και κύβου ως συνάρτηση της διαμέτρου της σφαίρας,

Θα καταλήξουμε φυσικά στο ίδιο αποτέλεσμα, ελαχιστοποίηση συνολικού όγκου για , και το ίδιο θα συμβεί και αν εκφράσουμε τον συνολικό όγκο ως συνάρτηση της ακμής του κύβου,
, και το ίδιο θα συμβεί και αν εκφράσουμε τον συνολικό όγκο ως συνάρτηση της ακμής του κύβου,

ΕΠΙΠΛΕΟΝ, ανάλογο (αλλά 'αντίστροφο') αποτέλεσμα σχύει και για το αντίστροφο πρόβλημα: αν ο συνολικός όγκος σφαίρας και κύβου είναι σταθερός (πχ ), τότε η συνολική επιφάνεια σφαίρας και κύβου μεγιστοποιείται για
), τότε η συνολική επιφάνεια σφαίρας και κύβου μεγιστοποιείται για  . Η προσέγγιση είναι απόλυτα ανάλογη προς αυτήν του αρχικού προβλήματος, οπότε δίνω απλώς τους σχετικούς τύπους
. Η προσέγγιση είναι απόλυτα ανάλογη προς αυτήν του αρχικού προβλήματος, οπότε δίνω απλώς τους σχετικούς τύπους

και

Όλα τα παραπάνω συνοψίζονται στο συνημμένο, που 'εξηγεί' και την επιλογή της διαμέτρου αντί της ακτίνας
σ' ευχαριστούμε για την ενασχόληση και το δυναμικό σχήμα, παραθέτω κι εγώ μια δική μου οπτική:
Γνωρίζοντας το υπέροχο αυτό αποτέλεσμα (άμεση γενίκευση σχολικού προβλήματος), ας κινηθούμε λίγο διαφορετικά, θέτοντας
 (συνολική επιφάνεια σφαίρας και κύβου) και εκφράζοντας τον συνολικό όγκο σφαίρας και κύβου ως συνάρτηση της διαμέτρου της σφαίρας,
(συνολική επιφάνεια σφαίρας και κύβου) και εκφράζοντας τον συνολικό όγκο σφαίρας και κύβου ως συνάρτηση της διαμέτρου της σφαίρας,
Θα καταλήξουμε φυσικά στο ίδιο αποτέλεσμα, ελαχιστοποίηση συνολικού όγκου για
 , και το ίδιο θα συμβεί και αν εκφράσουμε τον συνολικό όγκο ως συνάρτηση της ακμής του κύβου,
, και το ίδιο θα συμβεί και αν εκφράσουμε τον συνολικό όγκο ως συνάρτηση της ακμής του κύβου,
ΕΠΙΠΛΕΟΝ, ανάλογο (αλλά 'αντίστροφο') αποτέλεσμα σχύει και για το αντίστροφο πρόβλημα: αν ο συνολικός όγκος σφαίρας και κύβου είναι σταθερός (πχ
 ), τότε η συνολική επιφάνεια σφαίρας και κύβου μεγιστοποιείται για
), τότε η συνολική επιφάνεια σφαίρας και κύβου μεγιστοποιείται για  . Η προσέγγιση είναι απόλυτα ανάλογη προς αυτήν του αρχικού προβλήματος, οπότε δίνω απλώς τους σχετικούς τύπους
. Η προσέγγιση είναι απόλυτα ανάλογη προς αυτήν του αρχικού προβλήματος, οπότε δίνω απλώς τους σχετικούς τύπους
και

Όλα τα παραπάνω συνοψίζονται στο συνημμένο, που 'εξηγεί' και την επιλογή της διαμέτρου αντί της ακτίνας
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15767
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Σφαίρα και κύβος, επιφάνεια και όγκος
Ας την δούμε και στοιχειωδώς, χωρίς παραγώγιση. Θα χρησιμοποιήσω την ανισότητα
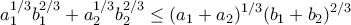 στους θετικούς, με ισότητα αν και μόνο αν
στους θετικούς, με ισότητα αν και μόνο αν  .
.
Πρόκειται για ειδική περίπτωση της Holder που αποδεικνύεται εύκολα υψώνοντας στον κύβο (και θέτοντας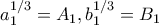 για να μην κουβαλάμε μεγάλες παραστάσεις).
για να μην κουβαλάμε μεγάλες παραστάσεις).
Έτσι

Οπότε
 (που είναι το ζητούμενο άθροισμα όγκων) με ισότητα αν και μόνον αν
(που είναι το ζητούμενο άθροισμα όγκων) με ισότητα αν και μόνον αν
 , ισοδύναμα
, ισοδύναμα 
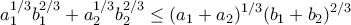 στους θετικούς, με ισότητα αν και μόνο αν
στους θετικούς, με ισότητα αν και μόνο αν  .
. Πρόκειται για ειδική περίπτωση της Holder που αποδεικνύεται εύκολα υψώνοντας στον κύβο (και θέτοντας
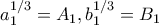 για να μην κουβαλάμε μεγάλες παραστάσεις).
για να μην κουβαλάμε μεγάλες παραστάσεις).Έτσι

Οπότε
 (που είναι το ζητούμενο άθροισμα όγκων) με ισότητα αν και μόνον αν
(που είναι το ζητούμενο άθροισμα όγκων) με ισότητα αν και μόνον αν  , ισοδύναμα
, ισοδύναμα 
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3344
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Σφαίρα και κύβος, επιφάνεια και όγκος
Ακρότατα άνευ ΛογισμούMihalis_Lambrou έγραψε: ↑Κυρ Μάιος 31, 2020 1:48 pmΑς την δούμε και στοιχειωδώς, χωρίς παραγώγιση. Θα χρησιμοποιήσω την ανισότητα
στους θετικούς, με ισότητα αν και μόνο αν
.
Πρόκειται για ειδική περίπτωση της Holder που αποδεικνύεται εύκολα υψώνοντας στον κύβο (και θέτονταςγια να μην κουβαλάμε μεγάλες παραστάσεις).
Έτσι
Οπότε
(που είναι το ζητούμενο άθροισμα όγκων) με ισότητα αν και μόνον αν
, ισοδύναμα

Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες
