 ικανοποιούν την
ικανοποιούν την 
Βρείτε τη μέγιστη και την ελάχιστη τιμή της ποσότητας :

Συντονιστής: Μπάμπης Στεργίου
 ικανοποιούν την
ικανοποιούν την 

Μία εκτός φακέλου
 και η ελάχιστη τιμή
και η ελάχιστη τιμή  .
. . Όμως, είναι
. Όμως, είναι  , οπότε
, οπότε  . Η ισότητα, προφανώς μπορεί να ισχύει (όταν
. Η ισότητα, προφανώς μπορεί να ισχύει (όταν  και
και  ).
). . Όμως, είναι
. Όμως, είναι  , οπότε
, οπότε  . Και εδώ η ισότητα προφανώς μπορεί να ισχύει.
. Και εδώ η ισότητα προφανώς μπορεί να ισχύει. γράφεται:
γράφεται: άρα
άρα ή
ή είναι η σχέση
είναι η σχέση 
 γίνεται
γίνεται ή
ή είναι η σχέση
είναι η σχέση 
 γίνεται
γίνεται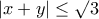 ή
ή είναι η σχέση
είναι η σχέση 
 γίνεται
γίνεται ή
ή ή
ή  ή
ή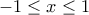 ή
ή  είναι η σχέση
είναι η σχέση 
 και
και  έχουμε:
έχουμε: ή
ή  ή
ή  ή
ή ή...ή
ή...ή  είναι η σχέση
είναι η σχέση 
 και
και  προκύπτει:
προκύπτει: οπότε
οπότε είναι:
είναι:
 είναι:
είναι:
Καλημέρα!nikhtas30 έγραψε: ↑Πέμ Σεπ 03, 2020 7:01 amΗ ποσότηταγράφεται:
άρα
ή
είναι η σχέση
Ηγίνεται
ή
είναι η σχέση
η σχέσηγίνεται
ή
είναι η σχέση
ηγίνεται
ή
ή
ή
ή
είναι η σχέση
Προσθέτωντας κατά μέλη τις σχέσειςκαι
έχουμε:
ή
ή
ή
ή...ή
είναι η σχέση
Προσθέτωντας κατά μέλη τις σχέσειςκαι
προκύπτει:
οπότε
Η ελάχιστη τιμή της ποσότηταςείναι:
Η μέγιστη τιμή της ποσότηταςείναι:

 και
και  μέτρων σε ύψος, που προφανώς είναι σωστό. Όταν προσθέτεις κατά μέλη χάνεται η ισοδυναμία οπότε δεν μπορείς να γυρίσεις τά βήματα προς τα πίσω και να δεις πότε και αν ισχύει η ισότητα.
μέτρων σε ύψος, που προφανώς είναι σωστό. Όταν προσθέτεις κατά μέλη χάνεται η ισοδυναμία οπότε δεν μπορείς να γυρίσεις τά βήματα προς τα πίσω και να δεις πότε και αν ισχύει η ισότητα.Ορέστης Λιγνός έγραψε: ↑Πέμ Σεπ 03, 2020 12:21 amΜία εκτός φακέλου
Ισχυρίζομαι ότι η μέγιστη τιμή είναικαι η ελάχιστη τιμή
.
Μέγιστη τιμή: Αρκεί να δείξουμε ότι. Όμως, είναι
, οπότε
. Η ισότητα, προφανώς μπορεί να ισχύει (όταν
και
).
Ελάχιστη τιμή: Αρκεί να δείξουμε ότι. Όμως, είναι
, οπότε
. Και εδώ η ισότητα προφανώς μπορεί να ισχύει.
Ορέστης Λιγνός έγραψε: ↑Πέμ Σεπ 03, 2020 12:21 amΜία εκτός φακέλου
Ισχυρίζομαι ότι η μέγιστη τιμή είναικαι η ελάχιστη τιμή
.
Μέγιστη τιμή: Αρκεί να δείξουμε ότι. Όμως, είναι
, οπότε
. Η ισότητα, προφανώς μπορεί να ισχύει (όταν
και
).
Ελάχιστη τιμή: Αρκεί να δείξουμε ότι. Όμως, είναι
, οπότε
. Και εδώ η ισότητα προφανώς μπορεί να ισχύει.
 νομίζω θα έπρεπε για κάθε
νομίζω θα έπρεπε για κάθε  :
: να μας οδηγεί σε άτοπο αλλά δεν μπήκες στην διαδικασία να το αποδείξεις, χωρίς να αμφισβητώ πως δεν μπορείς να το δείξεις αν θες.
να μας οδηγεί σε άτοπο αλλά δεν μπήκες στην διαδικασία να το αποδείξεις, χωρίς να αμφισβητώ πως δεν μπορείς να το δείξεις αν θες. να ισχύει, μαλλον το απέδειξες δυσκολεύομαι να παρακολουθήσω.
να ισχύει, μαλλον το απέδειξες δυσκολεύομαι να παρακολουθήσω. ή το
ή το  ;
;.
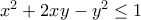 και μετά να αποδείξεις ότι δεν υπάρχει κάποιος μικρότερος αριθμός στην θέση του
και μετά να αποδείξεις ότι δεν υπάρχει κάποιος μικρότερος αριθμός στην θέση του  (δεξιά). Αυτό το πετυχαίνεις
(δεξιά). Αυτό το πετυχαίνεις έχεις ισότητα
έχεις ισότητα  . Το λοιπόν, αυτό ακριβώς έκανε ο Ορέστης. Είναι στο βήμα
. Το λοιπόν, αυτό ακριβώς έκανε ο Ορέστης. Είναι στο βήμα .
 και
και 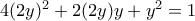 . Ποιες εϊναι αυτές οι τιμές των
. Ποιες εϊναι αυτές οι τιμές των  ; Μα είναι προφανές, όπως σωστά λέει η λύση του Ορέστη. Υπόδειξη: Η τελευταία γράφεται
; Μα είναι προφανές, όπως σωστά λέει η λύση του Ορέστη. Υπόδειξη: Η τελευταία γράφεται  .
. Σας ευχαριστώ για την διευκρίνιση κύριε ΛάμπρουMihalis_Lambrou έγραψε: ↑Πέμ Σεπ 03, 2020 9:46 am.
Νικήτα, το παραπάνω δεν είναι ακριβές. Είναι ένας τρόπος αλλά υπάρχει και δεύτερος. Συγκεκριμένα να αποδείξεις ότι
και μετά να αποδείξεις ότι δεν υπάρχει κάποιος μικρότερος αριθμός στην θέση του
(δεξιά). Αυτό το πετυχαίνεις
δίχνοντας ότι για κάποιες τιμές τωνέχεις ισότητα
. Το λοιπόν, αυτό ακριβώς έκανε ο Ορέστης. Είναι στο βήμα
..
Με άλλα λόγια ότανκαι
. Ποιες εϊναι αυτές οι τιμές των
; Μα είναι προφανές, όπως σωστά λέει η λύση του Ορέστη. Υπόδειξη: Η τελευταία γράφεται
.
Όμοια για το ελάχιστο.
Μετά την καταπληκτική λύση του Ορέστη με ύλη Α Λυκείου






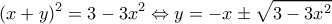

 με
με  όπου
όπου  για
για  και ελάχιστο
και ελάχιστο  για
για 

 .
. .
.
 .
.

 .
. με
με  .
. , βρίσκω ότι έχει ολικά ακρότατα τα
, βρίσκω ότι έχει ολικά ακρότατα τα 
 .
. και
και  , μπορούμε να εμφανίσουμε μια σχέση με μία μόνο μεταβλητή .
, μπορούμε να εμφανίσουμε μια σχέση με μία μόνο μεταβλητή . , σχηματίζουμε το κλάσμα
, σχηματίζουμε το κλάσμα 
 . Αν
. Αν  , διαιρούμε με
, διαιρούμε με  και αντικαθιστούμε
και αντικαθιστούμε  .
. με
με 
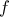 για
για 
 ) έχει μέγιστο το
) έχει μέγιστο το  και για
και για  (δηλαδή για
(δηλαδή για  ), ελάχιστο το
), ελάχιστο το  , κλπ .
, κλπ .Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 15 επισκέπτες