 , μελετήστε ως προς την μονοτονία
, μελετήστε ως προς την μονοτονία και τα ακρότατα , την συνάρτηση :

Συντονιστής: Μπάμπης Στεργίου
ΛΥΣΗ
 ορίζεται όταν
ορίζεται όταν  οπότε
οπότε  και είναι
και είναι  παραγωγίσιμη με
παραγωγίσιμη με 
 είναι
είναι  και τότε για
και τότε για 
 έτσι η
έτσι η  είναι γνήσια αύξουσα στ0
είναι γνήσια αύξουσα στ0  και είναι
και είναι  έτσι η
έτσι η  είναι γνήσια φθίνουσα στο
είναι γνήσια φθίνουσα στο 
 τώρα
τώρα  που για
που για  ανήκει στο
ανήκει στο  και τότε έχουμε τις περιπτώσεις:
και τότε έχουμε τις περιπτώσεις: η ρίζα
η ρίζα και τότε :
και τότε : άρα η
άρα η  και
και 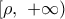
 άρα
άρα ![f\,\,\nearrow (0,\,\,\rho ] f\,\,\nearrow (0,\,\,\rho ]](/forum/ext/geomar/texintegr/latexrender/pictures/2e53921410aa2162896f525c6e9acc0a.png) επομένως στο
επομένως στο  παρουσιάζει ελάχιστο
παρουσιάζει ελάχιστο  η ρίζα
η ρίζα  και τότε :
και τότε : άρα
άρα 
 άρα η
άρα η  και
και 
 παρουσιάζει ελάχιστο
παρουσιάζει ελάχιστοΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες