abgd έγραψε: ↑Σάβ Απρ 22, 2023 7:52 pm
Με αφορμή
αυτή την άσκηση του Θανάση, ένα απαιτητικό θέμα...
Έστω η συνάρτηση
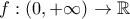
για την οποία γνωρίζουμε ότι:
- είναι δύο φορές παραγωγίσιμη με
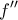 αρνητική,
αρνητική,
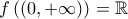 ,
,
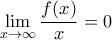 .
.
- υπάρχει
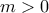 τέτοιο ώστε
τέτοιο ώστε 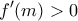
Να αποδειχθεί ότι από οποιοδήποτε σημείο
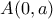
του άξονα

άγεται μοναδική εφαπτομένη στη γραφική παράσταση της συνάρτησης

.
A) Πρώτα θα βρούμε τα όρια της συνάρτησης στα
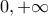
.
H

είναι γνησίως φθίνουσα επομένως στο
![(0,m] (0,m]](/forum/ext/geomar/texintegr/latexrender/pictures/9d063bac6e7fc814b125696ff1fb66be.png)
είναι θετική και η

γνησίως αύξουσα. Άρα
![f\left( \left( 0,m\right] \right) =\left( \lim\limits_{x\rightarrow 0^{+}}f\left( x\right) ,f\left( m\right) \right] f\left( \left( 0,m\right] \right) =\left( \lim\limits_{x\rightarrow 0^{+}}f\left( x\right) ,f\left( m\right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/e55103d5e537c7ecfa5eef059bfb295e.png)
Στο διάστημα
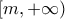
η

δε μπορεί να έχει ρίζα. Αν είχε κάποια

στο
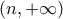
η

θα ήταν αρνητική και επομένως στο
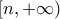
η

θα ήταν γνησίως φθίνουσα. Αλλά τότε θα είχαμε ότι
![f\left( \left[ n,+\infty \right) \right) =\left( \lim\limits_{x\rightarrow +\infty }f\left( x\right) ,f\left( n\right) \right] f\left( \left[ n,+\infty \right) \right) =\left( \lim\limits_{x\rightarrow +\infty }f\left( x\right) ,f\left( n\right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/132b8f9548435a065b864979e85a0ad9.png)
. Αφού, προφανώς, θα είναι
![f\left( \left[ m,n\right] \right) =\left[ f\left( m\right) ,f\left( n\right) \right] f\left( \left[ m,n\right] \right) =\left[ f\left( m\right) ,f\left( n\right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/0d79fd44c98a6e1ecfd11dd19c01cbd5.png)
έχουμε (ανεξάρτητα από το ποιές είναι οι τιμές των ορίων) ενώνοντας τα επιμέρους διαστήματα, το άτοπο συμπέρασμα ότι
![f\left( 0,+\infty \right) \subseteq \left( -\infty ,f\left( n\right) \right] f\left( 0,+\infty \right) \subseteq \left( -\infty ,f\left( n\right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/d1f5bdf1b30e90be6c5de490f97a331b.png)
. Συνεπώς η

δεν έχει ρίζα, άρα διατηρεί πρόσημο, επομένως είναι θετική και η

είναι γνησίως αύξουσα άρα
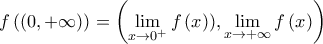
.
Αλλά από την υπόθεση το σύνολο τιμών της

είναι το

. Άρα έχουμε ότι
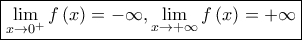
,
B) Στη συνέχεια αποδεικνύουμε ότι από το τυχόν

διέρχετα μοναδική εφαπτομένη της
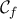
.
Ύπαρξη Για να υπάρχει εφαπτομένη
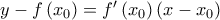
που διέρχεται από το

πέπει για κάποιο

να ισχύει
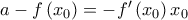
δηλαδή η παραγωγίσιμη συνάρτηση
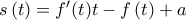
,
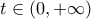
να έχει ρίζα.

Για
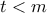
είναι
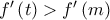
επομένως
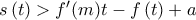
Αλλά
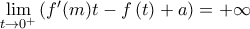
άρα και
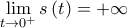
. Επομένως
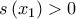
για κάποιο

.

Για

έχουμε
H

ως γνησίως φθίνουσα και συνεχής έχει όριο στο

που είναι το κάτω άκρο του διαστήματος
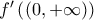
. Έστω

. Από την υπόθεση έχουμε
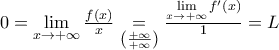
.
Λόγω του κοίλου της
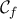
έχουμε ότι κάθε σημείο της βρίσκεται κάτω από την εφαπτομένη
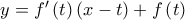
άρα αυτό ισχύει και για το σημείο
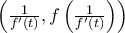
. Επομένως
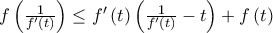
που μας δίνει την
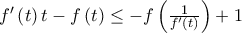
. Αλλά
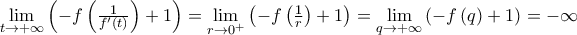
και επομένως και
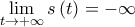
.
Άρα
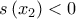
για κάποιο

,
Από το θεώρημα του Bolzano έχουμε ότι η

έχει μια τουλάχιστον ρίζα.
Μοναδικότητα Είναι
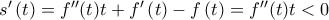
άρα η

είναι γνησίως φθίνουσα και η ρίζα της μοναδικη.
O Κώστας (abgd) είχε την καλοσύνη να μου επισημάνει με προσωπικό μήνυμα δύο λάθη εκ των οποίοων το ένα ήταν ουσιώδες και αφορούσε στον υπολογισμό του ορίου 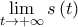 Τον ευχαριστώ πολύ. Προχώρησα σε επιδιόρθωση που ελπίζω να είναι η τελική.
Τον ευχαριστώ πολύ. Προχώρησα σε επιδιόρθωση που ελπίζω να είναι η τελική. 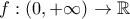 για την οποία γνωρίζουμε ότι:
για την οποία γνωρίζουμε ότι: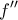 αρνητική,
αρνητική,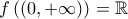 ,
,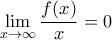 .
.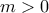 τέτοιο ώστε
τέτοιο ώστε 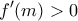
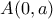 του άξονα
του άξονα  άγεται μοναδική εφαπτομένη στη γραφική παράσταση της συνάρτησης
άγεται μοναδική εφαπτομένη στη γραφική παράσταση της συνάρτησης  .
.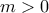 τέτοιο ώστε
τέτοιο ώστε 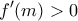



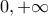 .
. είναι γνησίως φθίνουσα επομένως στο
είναι γνησίως φθίνουσα επομένως στο ![(0,m] (0,m]](/forum/ext/geomar/texintegr/latexrender/pictures/9d063bac6e7fc814b125696ff1fb66be.png) είναι θετική και η
είναι θετική και η  γνησίως αύξουσα. Άρα
γνησίως αύξουσα. Άρα ![f\left( \left( 0,m\right] \right) =\left( \lim\limits_{x\rightarrow 0^{+}}f\left( x\right) ,f\left( m\right) \right] f\left( \left( 0,m\right] \right) =\left( \lim\limits_{x\rightarrow 0^{+}}f\left( x\right) ,f\left( m\right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/e55103d5e537c7ecfa5eef059bfb295e.png)
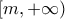 η
η  στο
στο 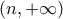 η
η 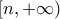 η
η ![f\left( \left[ n,+\infty \right) \right) =\left( \lim\limits_{x\rightarrow +\infty }f\left( x\right) ,f\left( n\right) \right] f\left( \left[ n,+\infty \right) \right) =\left( \lim\limits_{x\rightarrow +\infty }f\left( x\right) ,f\left( n\right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/132b8f9548435a065b864979e85a0ad9.png) . Αφού, προφανώς, θα είναι
. Αφού, προφανώς, θα είναι ![f\left( \left[ m,n\right] \right) =\left[ f\left( m\right) ,f\left( n\right) \right] f\left( \left[ m,n\right] \right) =\left[ f\left( m\right) ,f\left( n\right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/0d79fd44c98a6e1ecfd11dd19c01cbd5.png) έχουμε (ανεξάρτητα από το ποιές είναι οι τιμές των ορίων) ενώνοντας τα επιμέρους διαστήματα, το άτοπο συμπέρασμα ότι
έχουμε (ανεξάρτητα από το ποιές είναι οι τιμές των ορίων) ενώνοντας τα επιμέρους διαστήματα, το άτοπο συμπέρασμα ότι ![f\left( 0,+\infty \right) \subseteq \left( -\infty ,f\left( n\right) \right] f\left( 0,+\infty \right) \subseteq \left( -\infty ,f\left( n\right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/d1f5bdf1b30e90be6c5de490f97a331b.png) . Συνεπώς η
. Συνεπώς η 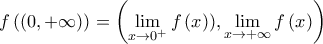 .
.  . Άρα έχουμε ότι
. Άρα έχουμε ότι 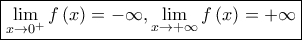 ,
, διέρχετα μοναδική εφαπτομένη της
διέρχετα μοναδική εφαπτομένη της 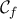 .
.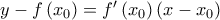 που διέρχεται από το
που διέρχεται από το  πέπει για κάποιο
πέπει για κάποιο  να ισχύει
να ισχύει 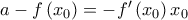 δηλαδή η παραγωγίσιμη συνάρτηση
δηλαδή η παραγωγίσιμη συνάρτηση 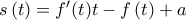 ,
, 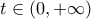
 Για
Για 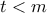 είναι
είναι 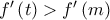 επομένως
επομένως 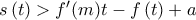
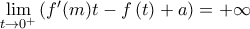 άρα και
άρα και 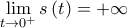 . Επομένως
. Επομένως 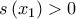 για κάποιο
για κάποιο  .
. έχουμε
έχουμε που είναι το κάτω άκρο του διαστήματος
που είναι το κάτω άκρο του διαστήματος 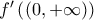 . Έστω
. Έστω  . Από την υπόθεση έχουμε
. Από την υπόθεση έχουμε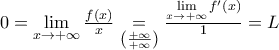 .
.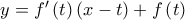 άρα αυτό ισχύει και για το σημείο
άρα αυτό ισχύει και για το σημείο 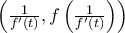 . Επομένως
. Επομένως 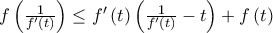 που μας δίνει την
που μας δίνει την 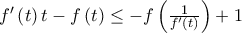 . Αλλά
. Αλλά 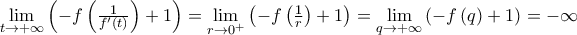 και επομένως και
και επομένως και 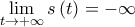 .
.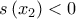 για κάποιο
για κάποιο  ,
,  έχει μια τουλάχιστον ρίζα.
έχει μια τουλάχιστον ρίζα. 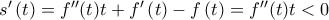 άρα η
άρα η 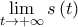 Τον ευχαριστώ πολύ. Προχώρησα σε επιδιόρθωση που ελπίζω να είναι η τελική.
Τον ευχαριστώ πολύ. Προχώρησα σε επιδιόρθωση που ελπίζω να είναι η τελική. 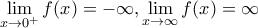
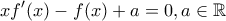

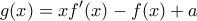
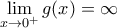
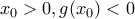
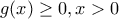

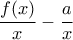 είναι αύξουσα .
είναι αύξουσα .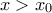 είναι
είναι 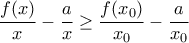
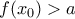 και παίρνοντας
και παίρνοντας 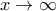
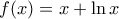 δεν ισχύει το συμπέρασμα.
δεν ισχύει το συμπέρασμα. στο σημείο
στο σημείο 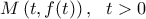 έχει εξίσωση:
έχει εξίσωση: 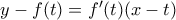 .
.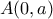 αν και μόνο αν
αν και μόνο αν 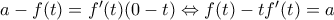 .
. άγεται μοναδική εφαπτομένη στην
άγεται μοναδική εφαπτομένη στην 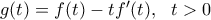 είναι
είναι  με σύνολο τιμών το
με σύνολο τιμών το  τότε
τότε 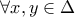 με
με 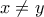 ισχύει:
ισχύει: 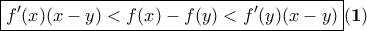 .
.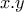 και της μονοτονίας της παραγώγου.
και της μονοτονίας της παραγώγου. με σύνολο τιμών το
με σύνολο τιμών το  τέτοιο ώστε
τέτοιο ώστε 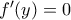 τότε από την
τότε από την 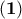 έχουμε:
έχουμε: 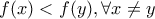 ή
ή 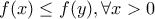
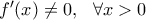 και έτσι η
και έτσι η  θα έχουμε:
θα έχουμε: 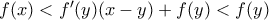 άτοπο. Άρα θα πρέπει
άτοπο. Άρα θα πρέπει 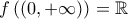 οπότε
οπότε 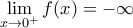 και
και 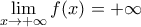
 είναι
είναι 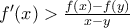 και αφού
και αφού 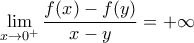 θα πρέπει:
θα πρέπει: 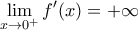
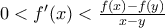 και αφού
και αφού 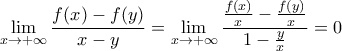 θα πρέπει:
θα πρέπει: 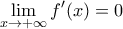
 τώρα έχουμε:
τώρα έχουμε: 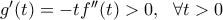 οπότε η
οπότε η 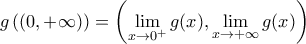
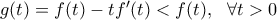 και
και 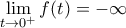 άρα θα είναι
άρα θα είναι 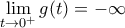
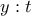 προκύπτει:
προκύπτει: 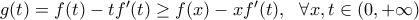
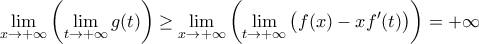
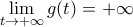 και συνεπώς
και συνεπώς 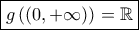
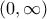 , οπότε
, οπότε 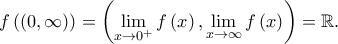
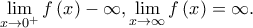
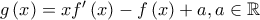 να έχει μοναδική ρίζα στο
να έχει μοναδική ρίζα στο 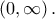
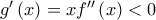 , άρα είναι γνησίως φθίνουσα στο
, άρα είναι γνησίως φθίνουσα στο 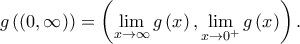
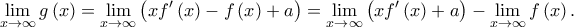
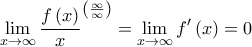 και
και 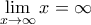 , επομένως από τον κανόνα de L' Hopital είναι
, επομένως από τον κανόνα de L' Hopital είναι 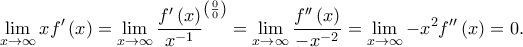
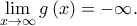
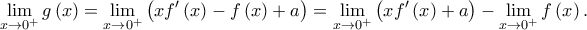
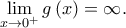
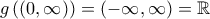 , άρα η
, άρα η 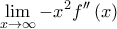 δεν ξέρουμε ούτε καν αν υπάρχει. Επομένως, δεν μπορούμε να κάνουμε DLH. Το άφησα όμως, καθώς ήθελα να βρω έναν συντομότερο υπολογισμό του ορίου σε σχέση με αυτόν που βρήκα στην αρχή και θεωρώ ότι έχει διδακτική αξία! [Στα παρακάτω, έχουμε δείξει από πριν ότι το όριο
δεν ξέρουμε ούτε καν αν υπάρχει. Επομένως, δεν μπορούμε να κάνουμε DLH. Το άφησα όμως, καθώς ήθελα να βρω έναν συντομότερο υπολογισμό του ορίου σε σχέση με αυτόν που βρήκα στην αρχή και θεωρώ ότι έχει διδακτική αξία! [Στα παρακάτω, έχουμε δείξει από πριν ότι το όριο 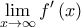 υπάρχει , άρα με DLH έχουμε
υπάρχει , άρα με DLH έχουμε 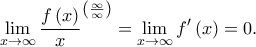 ]
] 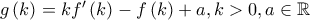 και είναι παραγωγίσιμη, συνεχής στο
και είναι παραγωγίσιμη, συνεχής στο 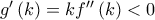 , άρα είναι γνησίως φθίνουσα στο
, άρα είναι γνησίως φθίνουσα στο 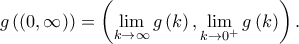
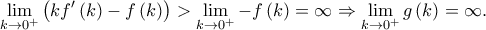
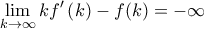 , τότε τελείωσα.
, τότε τελείωσα. βρίσκεται κάτω από την εφαπτομένη
βρίσκεται κάτω από την εφαπτομένη 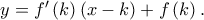
 το
το 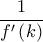 παίρνω
παίρνω 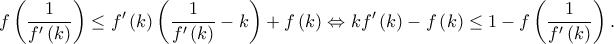
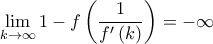 , τότε τελείωσα.
, τότε τελείωσα.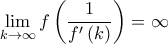 , τότε τελείωσα.
, τότε τελείωσα. 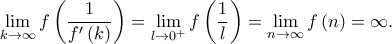
 είναι συνεχής, παραγωγίσιμη και γνησίως φθίνουσα στο
είναι συνεχής, παραγωγίσιμη και γνησίως φθίνουσα στο