 και
και  .
.*συν την συμμετρική αυτής
Συντονιστής: Μπάμπης Στεργίου
 και
και  .
.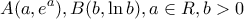
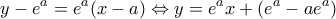 και
και 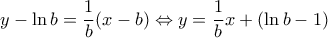
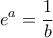 και
και 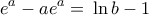 . Επομένως :
. Επομένως :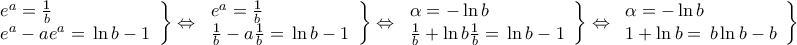
 , με
, με  ,
, 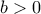 οι οποίοι ικανοποιούν και τις δυο εξισώσεις .
οι οποίοι ικανοποιούν και τις δυο εξισώσεις .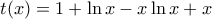 , με
, με 
 είναι συνεχής με
είναι συνεχής με 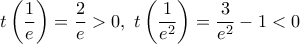
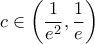 ώστε
ώστε 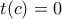
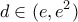 ώστε
ώστε 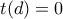
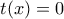 έχει δυο τουλάχιστον ρίζες .
έχει δυο τουλάχιστον ρίζες .  είναι δυο φορές παραγωγίσιμη με
είναι δυο φορές παραγωγίσιμη με 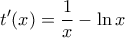 και
και 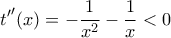 , οπότε η
, οπότε η 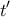 είναι γνησίως φθίνουσα .
είναι γνησίως φθίνουσα .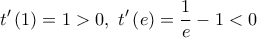 , επομένως από θεώρημα Bolzano έχουμε ότι υπάρχει
, επομένως από θεώρημα Bolzano έχουμε ότι υπάρχει 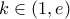 ώστε
ώστε 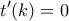 , όπου το
, όπου το  είναι μοναδικό λόγω μονοτονίας της
είναι μοναδικό λόγω μονοτονίας της 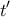 .
. είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 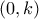 και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο 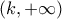 .
.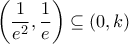 και
και 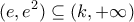 οι ρίζες
οι ρίζες 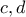 είναι μοναδικές .
είναι μοναδικές .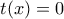 έχει δυο ακριβώς ρίζες , οπότε το σύστημα έχει δύο ακριβώς ζεύγη λύσεων , άρα υπάρχουν ακριβώς δύο εφαπτόμενες .
έχει δυο ακριβώς ρίζες , οπότε το σύστημα έχει δύο ακριβώς ζεύγη λύσεων , άρα υπάρχουν ακριβώς δύο εφαπτόμενες .Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες