(α) Αν
 είναι θετικός πραγματικός αριθμός, να αποδείξετε ότι:
είναι θετικός πραγματικός αριθμός, να αποδείξετε ότι: 
(β) Αν
 είναι θετικοί πραγματικοί αριθμοί, να αποδείξετε ότι:
είναι θετικοί πραγματικοί αριθμοί, να αποδείξετε ότι: 
Πρόβλημα 2
Δίνεται ορθογώνιο παραλληλόγραμμο
 , όπου
, όπου  . Πάνω στην πλευρά του
. Πάνω στην πλευρά του  παίρνουμε σημείο
παίρνουμε σημείο  , τέτοιο ώστε
, τέτοιο ώστε  και πάνω στην ημιευθεία
και πάνω στην ημιευθεία 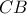 σημείο
σημείο  , τέτοιο ώστε
, τέτοιο ώστε  . Από το σημείο
. Από το σημείο  φέρουμε παράλληλη προς την
φέρουμε παράλληλη προς την 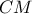 , η οποία τέμνει την ευθεία
, η οποία τέμνει την ευθεία  στο σημείο
στο σημείο  . Ονομάζουμε
. Ονομάζουμε  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών 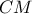 και
και  . Να αποδείξετε ότι:
. Να αποδείξετε ότι:(α)

(β) Τα σημεία
 και
και  ανήκουν στον ίδιο κύκλο.
ανήκουν στον ίδιο κύκλο.Πρόβλημα 3
Σε ένα τουρνουά καλαθόσφαιρας συμμετέχουν ομάδες μόνο από τη Λεμεσό και τη Λευκωσία. Οι ομάδες της Λευκωσίας είναι
 περισσότερες από αυτές της Λεμεσού. Κάθε δύο ομάδες συναντήθηκαν για παιχνίδι μεταξύ τους ακριβώς μια φορά. Η νικήτρια ομάδα πήρε
περισσότερες από αυτές της Λεμεσού. Κάθε δύο ομάδες συναντήθηκαν για παιχνίδι μεταξύ τους ακριβώς μια φορά. Η νικήτρια ομάδα πήρε  πόντο, η χαμένη ομάδα
πόντο, η χαμένη ομάδα  πόντους, ενώ δεν υπήρξαν ισοπαλίες. Όλες οι ομάδες από τη Λευκωσία μαζί συγκέντρωσαν
πόντους, ενώ δεν υπήρξαν ισοπαλίες. Όλες οι ομάδες από τη Λευκωσία μαζί συγκέντρωσαν  φορές περισσότερους πόντους από όλες τις ομάδες της Λεμεσού μαζί. Να βρείτε ποιος είναι ο μέγιστος δυνατός αριθμός των νικών της πιο επιτυχημένης ομάδας από τη Λεμεσό.
φορές περισσότερους πόντους από όλες τις ομάδες της Λεμεσού μαζί. Να βρείτε ποιος είναι ο μέγιστος δυνατός αριθμός των νικών της πιο επιτυχημένης ομάδας από τη Λεμεσό.Πρόβλημα 4
Να βρεθούν
 διαφορετικοί πρώτοι αριθμοί, οι οποίοι να διαιρούν τον αριθμό
διαφορετικοί πρώτοι αριθμοί, οι οποίοι να διαιρούν τον αριθμό  .
.
 έχει παράγοντα το
έχει παράγοντα το  . Ο πρώτος παράγοντας δείχνει ότι
. Ο πρώτος παράγοντας δείχνει ότι διαιρεί τον δοθέντα. Με λίγο χαρτί και μολύβι (και κριτήρια διαιρετότητας) εύκολα βρίσκουμε τους πρώτους παράγοντες
διαιρεί τον δοθέντα. Με λίγο χαρτί και μολύβι (και κριτήρια διαιρετότητας) εύκολα βρίσκουμε τους πρώτους παράγοντες  . Ο τρίτος μας δίνει τον
. Ο τρίτος μας δίνει τον  από όπου τσιμπάμε τους
από όπου τσιμπάμε τους  .
. είναι παραλληλόγραμμο, άρα
είναι παραλληλόγραμμο, άρα  και
και  Οπότε τα ορθογώνια τρίγωνα
Οπότε τα ορθογώνια τρίγωνα  είναι ίσα και
είναι ίσα και 
 είναι συμπληρωματικές, άρα
είναι συμπληρωματικές, άρα  οπότε
οπότε είναι ορθογώνιο και ισοσκελές, δηλαδή
είναι ορθογώνιο και ισοσκελές, δηλαδή  (ως εντός εναλλάξ). Αλλά και το
(ως εντός εναλλάξ). Αλλά και το 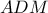
 που σημαίνει ότι το τετράπλευρο
που σημαίνει ότι το τετράπλευρο  είναι εγγράψιμο.
είναι εγγράψιμο.![\frac{(x^3-1)(x^3+1)(x^6+1)}{4}\geq \frac{x^3-1}{x}\Leftrightarrow x^1^0+x^7+x^4+x\geq 4\Leftrightarrow 4\sqrt[4]x^2^2\geq 4\Leftrightarrow x\geq 1 \frac{(x^3-1)(x^3+1)(x^6+1)}{4}\geq \frac{x^3-1}{x}\Leftrightarrow x^1^0+x^7+x^4+x\geq 4\Leftrightarrow 4\sqrt[4]x^2^2\geq 4\Leftrightarrow x\geq 1](/forum/ext/geomar/texintegr/latexrender/pictures/6f7a3c1620a36e5f6a3dde879f20e665.png) που αληθεύει αφού προφανώς η αρχική σχέση δεν ισχύει για
που αληθεύει αφού προφανώς η αρχική σχέση δεν ισχύει για 


 αρκεί
αρκεί  που ισχύει ,όμοια και για
που ισχύει ,όμοια και για 

 που ισχύει.
που ισχύει.
 του οποίου οι συντελεστές
του οποίου οι συντελεστές  , κατά φθίνουσα σειρά δυνάμεων, αλλάζουν πρόσημο δυο φορές. Άρα από το κανόνα των
, κατά φθίνουσα σειρά δυνάμεων, αλλάζουν πρόσημο δυο φορές. Άρα από το κανόνα των  θα έχει το πολύ δυο θετικές ρίζες
θα έχει το πολύ δυο θετικές ρίζες είναι ρίζα του
είναι ρίζα του  και
και  . Επόμενως το
. Επόμενως το  παρατηρούμε ότι
παρατηρούμε ότι  και εφόσον δεν υπάρχουν άλλες ρίζες πέραν του
και εφόσον δεν υπάρχουν άλλες ρίζες πέραν του  , με την ισότητα μόνο για
, με την ισότητα μόνο για 
 που αληθεύει αφού προφανώς
που αληθεύει αφού προφανώς διαιρεί τον
διαιρεί τον  . Επίσης από μικρό θεώρημα Fermat έχουμε ότι
. Επίσης από μικρό θεώρημα Fermat έχουμε ότι  και
και  για
για  . (Πρέπει να ελεγχθεί ότι οι
. (Πρέπει να ελεγχθεί ότι οι  και
και  δεν διαιρούνται με κανένα από αυτούς τους πρώτους.)
δεν διαιρούνται με κανένα από αυτούς τους πρώτους.)  αντί του
αντί του  .
.
 οι ομάδες της Λεμεσού,
οι ομάδες της Λεμεσού,  της Λευκωσίας. Έστω ακόμη,
της Λευκωσίας. Έστω ακόμη,  οι πόντοι των ομάδων της Λεμεσού, και
οι πόντοι των ομάδων της Λεμεσού, και  οι πόντοι των ομάδων της Λευκωσίας.
οι πόντοι των ομάδων της Λευκωσίας. παιχνίδια, οπότε οι συνολικοί πόντοι είναι
παιχνίδια, οπότε οι συνολικοί πόντοι είναι  .
.  .
. είναι περιττός, οπότε
είναι περιττός, οπότε  , οπότε
, οπότε  .
. , και άρα
, και άρα  .
. πόντους, άρα
πόντους, άρα  .
. .
. , τότε οι ομάδες της Λευκωσίας είναι
, τότε οι ομάδες της Λευκωσίας είναι  , και συγκέντρωσαν
, και συγκέντρωσαν  πόντους, ενώ της Λεμεσού είναι
πόντους, ενώ της Λεμεσού είναι  , συγκεντρώνοντας
, συγκεντρώνοντας  πόντους.
πόντους. πόντους, οπότε στα παιχνίδια με ομάδες της Λευκωσίας, συγκέντρωσαν
πόντους, οπότε στα παιχνίδια με ομάδες της Λευκωσίας, συγκέντρωσαν  (αν η συγκεκριμένη ομάδα νικήσει τις
(αν η συγκεκριμένη ομάδα νικήσει τις  , όμοια παίρνουμε σαν μέγιστο αριθμό νικών τις
, όμοια παίρνουμε σαν μέγιστο αριθμό νικών τις  .
. νίκες, και είναι εύκολο να κατασκευαστεί κατάλληλο παράδειγμα.
νίκες, και είναι εύκολο να κατασκευαστεί κατάλληλο παράδειγμα.