EGMO 2021
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
EGMO 2021
Από σήμερα ξεκινάει η EGMO 2021 με διοργανώτρια χώρα την Γεωργία. Όπως ανέφερα πρόσφατα η Ελλάδα είναι η μοναδική χώρα που δεν έστειλε εθνική ομάδα παρά τις φιλότιμες προσπάθειες της Ε.Μ.Ε. Θα ήθελα να ευχηθώ ολόψυχα καλή επιτυχία στις μαθήτριες της Κύπρου καθώς και στον δικό μας Δημήτρη Χριστοφίδη (Demetres) που θα είναι ο Leader της αποστολής! Όταν θα επιτραπεί από την επιτροπή αναμένουμε εδώ τα θέματα για να τα δούμε και οι υπόλοιποι 


Λέξεις Κλειδιά:
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: EGMO 2021
Καλησπέρα,
Σήμερα είχαμε την πρώτη ημέρα του διαγωνισμού. Όσο για τα θέματα πρέπει να κάνετε λίγη υπομονή μιας και μπορούμε να τα αναρτήσουμε από την Τρίτη το απόγευμα ( η ώρα 15:00) και μετά.
Σήμερα είχαμε την πρώτη ημέρα του διαγωνισμού. Όσο για τα θέματα πρέπει να κάνετε λίγη υπομονή μιας και μπορούμε να τα αναρτήσουμε από την Τρίτη το απόγευμα ( η ώρα 15:00) και μετά.
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: EGMO 2021
Τα θέματα του διαγωνισμού:
Πρόβλημα 1
Ο αριθμός είναι φανταστυπέροχος. Αν για κάποιον θετικό ακέραιο
είναι φανταστυπέροχος. Αν για κάποιον θετικό ακέραιο  , οποιοδήποτε από τα στοιχεία του συνόλου
, οποιοδήποτε από τα στοιχεία του συνόλου  είναι φανταστυπέροχο, τότε είναι όλα φανταστυπέροχα. Είναι ο αριθμός
είναι φανταστυπέροχο, τότε είναι όλα φανταστυπέροχα. Είναι ο αριθμός  απαραίτητα φανταστυπέροχος;
απαραίτητα φανταστυπέροχος;
Πρόβλημα 2
Να προσδιορίσετε όλες τις συναρτήσεις , τέτοιες ώστε να ισχύει η εξίσωση
, τέτοιες ώστε να ισχύει η εξίσωση

για όλους τους ρητούς αριθμούς και
και  .
.
Εδώ, το συμβολίζει το σύνολο των ρητών αριθμών.
συμβολίζει το σύνολο των ρητών αριθμών.
Πρόβλημα 3
Έστω τρίγωνο με τη γωνία
με τη γωνία  να είναι αμβλεία. Έστω
να είναι αμβλεία. Έστω  και
και  οι τομές της εξωτερικής διχοτόμου της γωνίας
οι τομές της εξωτερικής διχοτόμου της γωνίας  , με τα ύψη του τριγώνου
, με τα ύψη του τριγώνου  από τις κορυφές
από τις κορυφές  και
και  αντίστοιχα. Έστω
αντίστοιχα. Έστω  και
και  τα σημεία στα ευθύγραμμα τμήματα
τα σημεία στα ευθύγραμμα τμήματα  και
και  αντίστοιχα, τέτοια ώστε
αντίστοιχα, τέτοια ώστε  και
και  . Να αποδείξετε ότι τα σημεία
. Να αποδείξετε ότι τα σημεία  ,
,  ,
,  ,
,  είναι ομοκυκλικά, δηλαδή ανήκουν πάνω στον ίδιο κύκλο.
είναι ομοκυκλικά, δηλαδή ανήκουν πάνω στον ίδιο κύκλο.
Πρόβλημα 4
Έστω τρίγωνο με έγκεντρο
με έγκεντρο  και έστω
και έστω  ένα αυθαίρετο σημείο στην πλευρά
ένα αυθαίρετο σημείο στην πλευρά  . Η κάθετη ευθεία από το σημείο
. Η κάθετη ευθεία από το σημείο  στην ευθεία
στην ευθεία  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  . Η κάθετη ευθεία από το σημείο
. Η κάθετη ευθεία από το σημείο 
στην ευθεία τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  . Να αποδείξετε ότι το συμμετρικό του σημείου
. Να αποδείξετε ότι το συμμετρικό του σημείου  ως προς την ευθεία
ως προς την ευθεία  βρίσκεται πάνω στην ευθεία
βρίσκεται πάνω στην ευθεία  .
.
Πρόβλημα 5
Σε ένα επίπεδο υπάρχει ειδικό σημείο το οποίο ονομάζουμε αρχή των αξόνων. Έστω
το οποίο ονομάζουμε αρχή των αξόνων. Έστω  ένα σύνολο από
ένα σύνολο από  σημεία του επιπέδου, τέτοια ώστε
σημεία του επιπέδου, τέτοια ώστε
(i) δεν υπάρχουν τρία σημεία του πάνω στην ίδια ευθεία
πάνω στην ίδια ευθεία
(ii) δεν υπάρχουν δύο σημεία του πάνω σε ευθεία η οποία περνά από την αρχή των αξόνων.
πάνω σε ευθεία η οποία περνά από την αρχή των αξόνων.
Ένα τρίγωνο με κορυφές στο σύνολο ονομάζεται χοντρό, αν το
ονομάζεται χοντρό, αν το  είναι αυστηρά μέσα στο τρίγωνο. Να βρείτε το μέγιστο δυνατό πλήθος των χοντρών τριγώνων.
είναι αυστηρά μέσα στο τρίγωνο. Να βρείτε το μέγιστο δυνατό πλήθος των χοντρών τριγώνων.
Πρόβλημα 6
Υπάρχει μη αρνητικός ακέραιος αριθμός~ , για τον οποίο η εξίσωση
, για τον οποίο η εξίσωση

έχει περισσότερα από ένα εκατομμύριο ζεύγη λύσεων , όπου οι
, όπου οι  και
και  είναι θετικοί ακέραιοι;
είναι θετικοί ακέραιοι;
Η παράσταση συμβολίζει το ακέραιο μέρους του πραγματικού αριθμού
συμβολίζει το ακέραιο μέρους του πραγματικού αριθμού  . Έτσι,
. Έτσι,  ,
, ,
,  και
και  .
.
Πρόβλημα 1
Ο αριθμός
 είναι φανταστυπέροχος. Αν για κάποιον θετικό ακέραιο
είναι φανταστυπέροχος. Αν για κάποιον θετικό ακέραιο  , οποιοδήποτε από τα στοιχεία του συνόλου
, οποιοδήποτε από τα στοιχεία του συνόλου  είναι φανταστυπέροχο, τότε είναι όλα φανταστυπέροχα. Είναι ο αριθμός
είναι φανταστυπέροχο, τότε είναι όλα φανταστυπέροχα. Είναι ο αριθμός  απαραίτητα φανταστυπέροχος;
απαραίτητα φανταστυπέροχος;Πρόβλημα 2
Να προσδιορίσετε όλες τις συναρτήσεις
 , τέτοιες ώστε να ισχύει η εξίσωση
, τέτοιες ώστε να ισχύει η εξίσωση
για όλους τους ρητούς αριθμούς
 και
και  .
.Εδώ, το
 συμβολίζει το σύνολο των ρητών αριθμών.
συμβολίζει το σύνολο των ρητών αριθμών.Πρόβλημα 3
Έστω τρίγωνο
 με τη γωνία
με τη γωνία  να είναι αμβλεία. Έστω
να είναι αμβλεία. Έστω  και
και  οι τομές της εξωτερικής διχοτόμου της γωνίας
οι τομές της εξωτερικής διχοτόμου της γωνίας  , με τα ύψη του τριγώνου
, με τα ύψη του τριγώνου  από τις κορυφές
από τις κορυφές  και
και  αντίστοιχα. Έστω
αντίστοιχα. Έστω  και
και  τα σημεία στα ευθύγραμμα τμήματα
τα σημεία στα ευθύγραμμα τμήματα  και
και  αντίστοιχα, τέτοια ώστε
αντίστοιχα, τέτοια ώστε  και
και  . Να αποδείξετε ότι τα σημεία
. Να αποδείξετε ότι τα σημεία  ,
,  ,
,  ,
,  είναι ομοκυκλικά, δηλαδή ανήκουν πάνω στον ίδιο κύκλο.
είναι ομοκυκλικά, δηλαδή ανήκουν πάνω στον ίδιο κύκλο.Πρόβλημα 4
Έστω τρίγωνο
 με έγκεντρο
με έγκεντρο  και έστω
και έστω  ένα αυθαίρετο σημείο στην πλευρά
ένα αυθαίρετο σημείο στην πλευρά  . Η κάθετη ευθεία από το σημείο
. Η κάθετη ευθεία από το σημείο  στην ευθεία
στην ευθεία  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  . Η κάθετη ευθεία από το σημείο
. Η κάθετη ευθεία από το σημείο 
στην ευθεία
 τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  . Να αποδείξετε ότι το συμμετρικό του σημείου
. Να αποδείξετε ότι το συμμετρικό του σημείου  ως προς την ευθεία
ως προς την ευθεία  βρίσκεται πάνω στην ευθεία
βρίσκεται πάνω στην ευθεία  .
.Πρόβλημα 5
Σε ένα επίπεδο υπάρχει ειδικό σημείο
 το οποίο ονομάζουμε αρχή των αξόνων. Έστω
το οποίο ονομάζουμε αρχή των αξόνων. Έστω  ένα σύνολο από
ένα σύνολο από  σημεία του επιπέδου, τέτοια ώστε
σημεία του επιπέδου, τέτοια ώστε(i) δεν υπάρχουν τρία σημεία του
 πάνω στην ίδια ευθεία
πάνω στην ίδια ευθεία(ii) δεν υπάρχουν δύο σημεία του
 πάνω σε ευθεία η οποία περνά από την αρχή των αξόνων.
πάνω σε ευθεία η οποία περνά από την αρχή των αξόνων. Ένα τρίγωνο με κορυφές στο σύνολο
 ονομάζεται χοντρό, αν το
ονομάζεται χοντρό, αν το  είναι αυστηρά μέσα στο τρίγωνο. Να βρείτε το μέγιστο δυνατό πλήθος των χοντρών τριγώνων.
είναι αυστηρά μέσα στο τρίγωνο. Να βρείτε το μέγιστο δυνατό πλήθος των χοντρών τριγώνων.Πρόβλημα 6
Υπάρχει μη αρνητικός ακέραιος αριθμός~
 , για τον οποίο η εξίσωση
, για τον οποίο η εξίσωση
έχει περισσότερα από ένα εκατομμύριο ζεύγη λύσεων
 , όπου οι
, όπου οι  και
και  είναι θετικοί ακέραιοι;
είναι θετικοί ακέραιοι;Η παράσταση
 συμβολίζει το ακέραιο μέρους του πραγματικού αριθμού
συμβολίζει το ακέραιο μέρους του πραγματικού αριθμού  . Έτσι,
. Έτσι,  ,
, ,
,  και
και  .
.- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: EGMO 2021
Για ευκολία στην πληκτρολόγηση γράφω αντί για φανταστυπέροχος απλά καλός.
Θα δείξουμε ότι κάθε φυσικός αριθμός είναι καλός. Επίσης μπορούμε να αντικαταστήσουμε το
 με οποιονδήποτε φυσικό
με οποιονδήποτε φυσικό  .
.Ισχυρισμός 1: O
 είναι καλός, αν και μόνο αν ο
είναι καλός, αν και μόνο αν ο  είναι καλός.
είναι καλός.Απόδειξη: Γράφω
 για να δηλώσω ότι αν ο
για να δηλώσω ότι αν ο  είναι καλός τότε είναι και ο
είναι καλός τότε είναι και ο  , και τούμπαλιν.
, και τούμπαλιν.Είναι,

 .
.Ισχυρισμός 2: O
 είναι καλός, αν και μόνο αν ο
είναι καλός, αν και μόνο αν ο  είναι καλός.
είναι καλός.Απόδειξη: Είναι,


Από τους Ισχυρισμούς 1 και 2, έχουμε ότι για κάθε καλό αριθμό, υπάρχει πάντα ένας μικρότερός του, άρα αφού ο
 είναι καλός, συμπεραίνουμε ότι και ο
είναι καλός, συμπεραίνουμε ότι και ο  είναι καλός. Από τους Ισχυρισμούς 1 και 2 τώρα, προκύπτει ότι κάθε φυσικός είναι καλός, άρα η απόδειξη ολοκληρώθηκε.
είναι καλός. Από τους Ισχυρισμούς 1 και 2 τώρα, προκύπτει ότι κάθε φυσικός είναι καλός, άρα η απόδειξη ολοκληρώθηκε. Κερδίζουμε ό,τι τολμούμε!
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: EGMO 2021
Έστω
 η δοσμένη σχέση.
η δοσμένη σχέση. Ισχυρισμός: Η
 είναι επί.
είναι επί.Απόδειξη: Έστω
 και
και  το σύνολο τιμών της
το σύνολο τιμών της  . Παρατηρούμε από την
. Παρατηρούμε από την  ότι αν
ότι αν  , για κάθε
, για κάθε  φυσικό και
φυσικό και  ρητό.
ρητό.Άρα, αν είναι
 , παρατηρούμε ότι
, παρατηρούμε ότι  , οπότε το
, οπότε το 
 .
.Ισχυρισμός 2:
 .
.Απόδειξη: Έστω
 , τέτοιο ώστε
, τέτοιο ώστε  . Τότε η
. Τότε η  δίνει
δίνει 

Ισχυρισμός 3:
 .
.Απόδειξη: Η
 δίνει
δίνει  , άρα συγκρίνοντας τις
, άρα συγκρίνοντας τις  και
και  έχουμε το ζητούμενο
έχουμε το ζητούμενο 
Έστω χωρίς βλάβη της γενικότητας ότι
 . Τότε, η
. Τότε, η  δίνει
δίνει  , δηλαδή η
, δηλαδή η  είναι η ταυτοτική στο
είναι η ταυτοτική στο  .
.Επιπλέον, παίρνοντας διαδοχικά
 στην αρχική προκύπτει
στην αρχική προκύπτει  για κάθε
για κάθε  ρητό και για κάθε
ρητό και για κάθε  φυσικό.
φυσικό.Σταθεροποιώντας τώρα το
 και παίρνοντας
και παίρνοντας  τέτοιο ώστε
τέτοιο ώστε  έχουμε ότι
έχουμε ότι  άρα
άρα  για κάθε
για κάθε  .
.Όμοια εργαζόμαστε αν
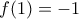 , οπότε προκύπτει η λύση
, οπότε προκύπτει η λύση  .
.Και οι δύο συναρτήσεις ικανοποιούν, άρα είναι και οι μοναδικές λύσεις.
Κερδίζουμε ό,τι τολμούμε!
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: EGMO 2021
BashDemetres έγραψε: ↑Τρί Απρ 13, 2021 5:11 pmΠρόβλημα 3: Έστω τρίγωνομε τη γωνία
να είναι αμβλεία. Έστω
και
οι τομές της εξωτερικής διχοτόμου της γωνίας
, με τα ύψη του τριγώνου
από τις κορυφές
και
αντίστοιχα. Έστω
και
τα σημεία στα ευθύγραμμα τμήματα
και
αντίστοιχα, τέτοια ώστε
και
. Να αποδείξετε ότι τα σημεία
,
,
,
είναι ομοκυκλικά, δηλαδή ανήκουν πάνω στον ίδιο κύκλο.
Είναι,
 και
και  , άρα τα τρίγωνα
, άρα τα τρίγωνα  είναι όμοια.
είναι όμοια.Συνεπώς,
 , οπότε
, οπότε  , που δίνει
, που δίνει  (*).
(*).Είναι, όμως,
 , και όμοια
, και όμοια  .
.Άρα,
 , άρα από την (*),
, άρα από την (*),  .
.Τελικά,
 , άρα
, άρα  , που δίνει άμεσα ότι τα
, που δίνει άμεσα ότι τα  είναι ομοκυκλικά.
είναι ομοκυκλικά. Κερδίζουμε ό,τι τολμούμε!
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: EGMO 2021
Αποδεικνύουμε τον επόμενο Ισχυρισμό:Demetres έγραψε: ↑Τρί Απρ 13, 2021 5:11 pmΠρόβλημα 4: Έστω τρίγωνομε έγκεντρο
και έστω
ένα αυθαίρετο σημείο στην πλευρά
. Η κάθετη ευθεία από το σημείο
στην ευθεία
τέμνει την ευθεία
στο σημείο
. Η κάθετη ευθεία από το σημείο

στην ευθείατέμνει την ευθεία
στο σημείο
. Να αποδείξετε ότι το συμμετρικό του σημείου
ως προς την ευθεία
βρίσκεται πάνω στην ευθεία
.
Ισχυρισμός: Τα τρίγωνα
 και
και  είναι όμοια.
είναι όμοια.Απόδειξη: Αφού
 , αρκεί να δείξουμε ότι
, αρκεί να δείξουμε ότι  , το οποίο ισχύει, καθώς
, το οποίο ισχύει, καθώς  (είναι
(είναι  )
) 
Άρα, από τον Ισχυρισμό,
 ,
,άρα
 , όπου η τελευταία ισότητα ισχύει διότι το
, όπου η τελευταία ισότητα ισχύει διότι το  είναι ορθόκεντρο του τριγώνου
είναι ορθόκεντρο του τριγώνου  .
.Άρα,
 , που δίνει ότι το
, που δίνει ότι το  είναι εγγράψιμο, άρα
είναι εγγράψιμο, άρα  και όμοια
και όμοια 
Έστω τώρα
 το σημείο όπου ο περιγεγραμμένος κύκλος του τριγώνου
το σημείο όπου ο περιγεγραμμένος κύκλος του τριγώνου  τέμνει την
τέμνει την  (αν εφάπτεται τότε το τρίγωνο είναι ισοσκελές - δεν αλλάζει κάτι στην απόδειξη καθώς τότε το
(αν εφάπτεται τότε το τρίγωνο είναι ισοσκελές - δεν αλλάζει κάτι στην απόδειξη καθώς τότε το  είναι το συμμετρικό του
είναι το συμμετρικό του  ως προς την
ως προς την  ).
).Τότε, είναι
 και όμοια
και όμοια  , άρα τα τρίγωνα
, άρα τα τρίγωνα  είναι ίσα, συνεπώς το
είναι ίσα, συνεπώς το  είναι το συμμετρικό του
είναι το συμμετρικό του  ως προς την
ως προς την  .
.Αφού
 , τελειώσαμε.
, τελειώσαμε. Κερδίζουμε ό,τι τολμούμε!
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: EGMO 2021
Η απάντηση είναι ναι.
Έστω
 ένας πολύ μεγάλος φυσικός, και
ένας πολύ μεγάλος φυσικός, και  η παράσταση του αριστερού μέλους.
η παράσταση του αριστερού μέλους.Θεωρούμε τα ζεύγη
 τέτοια ώστε
τέτοια ώστε  και
και  , καθώς και τις πιθανές τιμές της παράστασης
, καθώς και τις πιθανές τιμές της παράστασης  .
.Ο στόχος είναι, εάν
 ο αριθμός αυτών των ζευγών και
ο αριθμός αυτών των ζευγών και  οι πιθανές τιμές της παράστασης, το
οι πιθανές τιμές της παράστασης, το  να τείνει στο
να τείνει στο  καθώς το
καθώς το  μεγαλώνει. Τότε, θα έχουμε το ζητούμενο καθώς για κάποιο συγκεκριμένο μεγάλο
μεγαλώνει. Τότε, θα έχουμε το ζητούμενο καθώς για κάποιο συγκεκριμένο μεγάλο  από την αρχή του περιστερώνα θα υπάρχει τουλάχιστον ένα
από την αρχή του περιστερώνα θα υπάρχει τουλάχιστον ένα  τέτοιο ώστε η παράσταση
τέτοιο ώστε η παράσταση  να λαμβάνει την ίδια τιμή τουλάχιστον
να λαμβάνει την ίδια τιμή τουλάχιστον  φορές.
φορές.Bound για το
 : Για κάθε
: Για κάθε  , υπάρχουν
, υπάρχουν ![[\sqrt{f(m)] [\sqrt{f(m)]](/forum/ext/geomar/texintegr/latexrender/pictures/9a6c44a30d6135d3d7cac5d162c8ef5e.png) τιμές του
τιμές του  ώστε να ισχύει
ώστε να ισχύει  . Αφού όμως
. Αφού όμως  για κάθε
για κάθε  , υπάρχουν τουλάχιστον
, υπάρχουν τουλάχιστον ![[\sqrt{m}] [\sqrt{m}]](/forum/ext/geomar/texintegr/latexrender/pictures/edf8648092c0b491ac0ed5aa517f5af2.png) τιμές, ή αθροίζοντας από το
τιμές, ή αθροίζοντας από το  ως το
ως το  , τουλάχιστον
, τουλάχιστον ![[\sqrt{1}]+[\sqrt{2}]+\ldots+[\sqrt{k}] [\sqrt{1}]+[\sqrt{2}]+\ldots+[\sqrt{k}]](/forum/ext/geomar/texintegr/latexrender/pictures/8fd6e4b8ad4a023f36e32846702a2a1f.png) τιμές.
τιμές.Αποδεικνύουμε τον επόμενο Ισχυρισμό:
Ισχυρισμός:
![[\sqrt{1}]+[\sqrt{2}]+\ldots+[\sqrt{k}] \geq \dfrac{\sqrt{k^3}}{2} [\sqrt{1}]+[\sqrt{2}]+\ldots+[\sqrt{k}] \geq \dfrac{\sqrt{k^3}}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/451a442cd0f50fdfa274d4320b434562.png) για κάθε μεγάλο
για κάθε μεγάλο  .
.Απόδειξη: Επαγωγικά. Για
 ισχύει. Αν ισχύει για
ισχύει. Αν ισχύει για  τότε για
τότε για  αρκεί
αρκεί ![[\sqrt{s+1}] +\sqrt{s^3} \geq \sqrt{(s+1)^3} [\sqrt{s+1}] +\sqrt{s^3} \geq \sqrt{(s+1)^3}](/forum/ext/geomar/texintegr/latexrender/pictures/c0717f5a2a3895829891526015ad6d49.png) , ή ότι
, ή ότι  , που για μεγάλα
, που για μεγάλα  ισχύει
ισχύει  .
.(Motivation για τον Ισχυρισμό: Ψάχνουμε κάτω φράγμα για το άθροισμα. Κατά προτίμηση θα θέλαμε μια δύναμη του
 , ίσως μαζί με μια σταθερά, δηλαδή κάτι της μορφής
, ίσως μαζί με μια σταθερά, δηλαδή κάτι της μορφής  . Το
. Το  είναι πολύ χαλαρό και δεν κάνει την δουλειά πιο κάτω. Το
είναι πολύ χαλαρό και δεν κάνει την δουλειά πιο κάτω. Το  σαν φράγμα είναι πολύ ισχυρό για να ισχύει, άρα πάμε στην ''μέση λύση'', δηλαδή
σαν φράγμα είναι πολύ ισχυρό για να ισχύει, άρα πάμε στην ''μέση λύση'', δηλαδή  , και στη συνέχεια προσθέτουμε και μια σταθερά για να ισχύει για μεγάλα
, και στη συνέχεια προσθέτουμε και μια σταθερά για να ισχύει για μεγάλα  η ανισότητα)
η ανισότητα)Οπότε, υπάρχουν σίγουρα τουλάχιστον
 ζεύγη για μεγάλα
ζεύγη για μεγάλα  .
.Bound για το
 : Έστω
: Έστω  για κάθε
για κάθε  . Αποδεικνύουμε το εξής:
. Αποδεικνύουμε το εξής:Ισχυρισμός:
 για κάθε
για κάθε  .
.Απόδειξη: Επαγωγικά. Για
 ισχύει. Αν ισχύει για
ισχύει. Αν ισχύει για  , τότε για
, τότε για  αρκεί
αρκεί  , δηλαδή ότι
, δηλαδή ότι  .
.Έστω
 . Από το Θ.Μ.Τ στο
. Από το Θ.Μ.Τ στο  υπάρχει
υπάρχει  ώστε
ώστε  . Όμως, είναι
. Όμως, είναι  , και η απόδειξη ολοκληρώθηκε
, και η απόδειξη ολοκληρώθηκε  .
.Είναι λοιπόν,
 , συνεπώς και
, συνεπώς και  , δηλαδή υπάρχουν το πολύ
, δηλαδή υπάρχουν το πολύ  πιθανές τιμές.
πιθανές τιμές.Στο πρόβλημα, ο λόγος
 για μεγάλα
για μεγάλα  είναι
είναι  , και με DLH προκύπτει ότι το όριο
, και με DLH προκύπτει ότι το όριο  ισούται με
ισούται με  άρα έχουμε το ζητούμενο, καθώς για επαρκώς μεγάλο
άρα έχουμε το ζητούμενο, καθώς για επαρκώς μεγάλο  θα ισχύει ότι
θα ισχύει ότι  .
. Κερδίζουμε ό,τι τολμούμε!
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: EGMO 2021
Ας ονομάσουμε ένα τρίγωνο λεπτό όταν δεν είναι χοντρό.Demetres έγραψε: ↑Τρί Απρ 13, 2021 5:11 pmΠρόβλημα 5: Σε ένα επίπεδο υπάρχει ειδικό σημείοτο οποίο ονομάζουμε αρχή των αξόνων. Έστω
ένα σύνολο από
σημεία του επιπέδου, τέτοια ώστε
(i) δεν υπάρχουν τρία σημεία τουπάνω στην ίδια ευθεία
(ii) δεν υπάρχουν δύο σημεία τουπάνω σε ευθεία η οποία περνά από την αρχή των αξόνων.
Ένα τρίγωνο με κορυφές στο σύνολοονομάζεται χοντρό, αν το
είναι αυστηρά μέσα στο τρίγωνο. Να βρείτε το μέγιστο δυνατό πλήθος των χοντρών τριγώνων.
Αρκεί να βρούμε το ελάχιστο πλήθος των λεπτών τριγώνων.
Έστω
 ένα τυχαίο σημείο. Η ευθεία
ένα τυχαίο σημείο. Η ευθεία  χωρίζει το επίπεδο σε 2 ημιεπίπεδα. Έστω πως το αριστερό ημιεπίπεδο εχει
χωρίζει το επίπεδο σε 2 ημιεπίπεδα. Έστω πως το αριστερό ημιεπίπεδο εχει  σημεία
σημεία  και το δεξί έχει
και το δεξί έχει  σημεία
σημεία  .
.Είναι προφανές, ότι αν δύο σημεία
 ανήκουν και τα δύο στο
ανήκουν και τα δύο στο  ή και τα δύο στο
ή και τα δύο στο  , το τρίγωνο
, το τρίγωνο  είναι λεπτό.
είναι λεπτό.Άρα, το πλήθος των λεπτών τριγώνων που έχουν ως κορυφή το
 είναι
είναι  , και αφού η
, και αφού η  είναι κυρτή, έχουμε από Jensen
είναι κυρτή, έχουμε από Jensen  .
.Εργαζόμενοι όμοια για κάθε ένα από τα
 σημεία, έχουμε τουλάχιστον
σημεία, έχουμε τουλάχιστον  λεπτά τρίγωνα.
λεπτά τρίγωνα.Όμως, κάθε λεπτό τρίγωνο έχει μετρηθεί 2 φορές. Πράγματι, αν το
 είναι λεπτό τρίγωνο με τα
είναι λεπτό τρίγωνο με τα  στο αριστερό ημιεπίπεδο της
στο αριστερό ημιεπίπεδο της  και το
και το  πιο αριστερά από το
πιο αριστερά από το  , τότε το
, τότε το  θα προέκυπτε και αν εργαζόμασταν με κορυφή την
θα προέκυπτε και αν εργαζόμασταν με κορυφή την  , καθώς τότε τα
, καθώς τότε τα  ανήκουν στο δεξί ημιεπίπεδο της
ανήκουν στο δεξί ημιεπίπεδο της 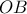 .
.Άρα, ο αριθμός των λεπτών τριγώνων είναι
 , οπότε τα χοντρά τρίγωνα είναι το πολύ
, οπότε τα χοντρά τρίγωνα είναι το πολύ  .
.Μένει να κατασκευάσουμε ένα παράδειγμα που να δείχνει ότι είναι εφικτό να έχουμε ακριβώς
 χοντρά τρίγωνα.
χοντρά τρίγωνα.Αυτό είναι απλό, παίρνοντας ένα κανονικό
 γωνο.
γωνο. Κερδίζουμε ό,τι τολμούμε!
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13272
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: EGMO 2021
ΈστωDemetres έγραψε: ↑Τρί Απρ 13, 2021 5:11 pmΤα θέματα του διαγωνισμού:
Πρόβλημα 3
Έστω τρίγωνομε τη γωνία
να είναι αμβλεία. Έστω
και
οι τομές της εξωτερικής διχοτόμου της γωνίας
, με τα ύψη του τριγώνου
από τις κορυφές
και
αντίστοιχα. Έστω
και
τα σημεία στα ευθύγραμμα τμήματα
και
αντίστοιχα, τέτοια ώστε
και
. Να αποδείξετε ότι τα σημεία
,
,
,
είναι ομοκυκλικά, δηλαδή ανήκουν πάνω στον ίδιο κύκλο.
 τα ύψη και
τα ύψη και  το ορθόκεντρο του
το ορθόκεντρο του  Γράφω τον περίκυκλο του
Γράφω τον περίκυκλο του  που τέμνει τις
που τέμνει τις  στα
στα  αντίστοιχα. Θα δείξω ότι
αντίστοιχα. Θα δείξω ότι  και
και  που είναι ισοδύναμο με το αρχικό πρόβλημα.
Τα ορθογώνια τρίγωνα
που είναι ισοδύναμο με το αρχικό πρόβλημα.
Τα ορθογώνια τρίγωνα  είναι ισογώνια. Άρα,
είναι ισογώνια. Άρα,  O περίκυκλος του
O περίκυκλος του  τέμνει την
τέμνει την  στο
στο  οπότε
οπότε  άρα το
άρα το  είναι το ορθόκεντρο του
είναι το ορθόκεντρο του  οπότε
οπότε 
 Αλλά από τα εγγεγραμμένα τετράπλευρα
Αλλά από τα εγγεγραμμένα τετράπλευρα  είναι:
είναι: που σημαίνει ότι και το
που σημαίνει ότι και το  είναι εγγράψιμο δηλαδή
είναι εγγράψιμο δηλαδή  Ομοίως αποδεικνύεται ότι
Ομοίως αποδεικνύεται ότι  και ολοκληρώνεται η απόδειξη.
και ολοκληρώνεται η απόδειξη.- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: EGMO 2021
Πρόβλημα 4: Δίνω μια άλλη λύση που έκανε ο Ισραηλίτης αρχηγός:
Το σημείο είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου  . Επειδή το
. Επειδή το  βρίσκεται στην
βρίσκεται στην  , από το αντίστροφο του θεωρήματος Steiner, οι συμμετρικές ευθείες της
, από το αντίστροφο του θεωρήματος Steiner, οι συμμετρικές ευθείες της  ως προς τις
ως προς τις  συντρέχουν (σε σημείο του περιγεγραμμένου κύκλου του τριγώνου
συντρέχουν (σε σημείο του περιγεγραμμένου κύκλου του τριγώνου  ). Οι συμμετρικές της
). Οι συμμετρικές της  ως προς τις
ως προς τις  και
και  είναι η
είναι η  και η
και η  . Άρα η συμμετρική της
. Άρα η συμμετρική της  ως προς την
ως προς την  περνά από το
περνά από το  . Δηλαδή το συμμετρικό του
. Δηλαδή το συμμετρικό του  ως προς την
ως προς την  ανήκει στην
ανήκει στην  όπως θέλαμε να δείξουμε.
όπως θέλαμε να δείξουμε.
Το σημείο
 είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου  . Επειδή το
. Επειδή το  βρίσκεται στην
βρίσκεται στην  , από το αντίστροφο του θεωρήματος Steiner, οι συμμετρικές ευθείες της
, από το αντίστροφο του θεωρήματος Steiner, οι συμμετρικές ευθείες της  ως προς τις
ως προς τις  συντρέχουν (σε σημείο του περιγεγραμμένου κύκλου του τριγώνου
συντρέχουν (σε σημείο του περιγεγραμμένου κύκλου του τριγώνου  ). Οι συμμετρικές της
). Οι συμμετρικές της  ως προς τις
ως προς τις  και
και  είναι η
είναι η  και η
και η  . Άρα η συμμετρική της
. Άρα η συμμετρική της  ως προς την
ως προς την  περνά από το
περνά από το  . Δηλαδή το συμμετρικό του
. Δηλαδή το συμμετρικό του  ως προς την
ως προς την  ανήκει στην
ανήκει στην  όπως θέλαμε να δείξουμε.
όπως θέλαμε να δείξουμε.- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: EGMO 2021
Άλλη μια λύση για το Πρόβλημα 5:
Μπορούμε να υποθέσουμε ότι τα σημεία του
του  βρίσκονται πάνω σε κύκλο, έστω ακτίνας
βρίσκονται πάνω σε κύκλο, έστω ακτίνας  . (Γιατί;) Για
. (Γιατί;) Για  ορίζουμε
ορίζουμε  ως το μήκος του τόξου που ξεκινάει από το
ως το μήκος του τόξου που ξεκινάει από το  και καταλήγει στο
και καταλήγει στο  πηγαίνοντας αντιωρολογιακά. Ορίζουμε το
πηγαίνοντας αντιωρολογιακά. Ορίζουμε το  να είναι ίσο με
να είναι ίσο με  αν
αν  και ίσο με
και ίσο με  σε διαφορετική περίπτωση.
σε διαφορετική περίπτωση.
Παρατηρούμε ότι και για κάθε
και για κάθε  η ποσότητα
η ποσότητα  είναι ίση με
είναι ίση με 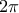 ή
ή  αναλόγως του αν το τρίγωνο
αναλόγως του αν το τρίγωνο  είναι χοντρό ή λεπτό.
είναι χοντρό ή λεπτό.
Έτσι έχουμε

Με τους δείκτες modulo , για κάθε
, για κάθε  , έχουμε ότι το
, έχουμε ότι το  εμφανίζεται
εμφανίζεται  φορές στο πιο πάνω άθροισμα και άρα το
φορές στο πιο πάνω άθροισμα και άρα το  εμφανίζεται
εμφανίζεται  φορές. Προσθέτοντας αυτά τα δύο έχουμε
φορές. Προσθέτοντας αυτά τα δύο έχουμε  .
.
Έτσι έχουμε

Αυτό ισχύει διότι στο πάμε
πάμε  φορές γύρω από τον κύκλο.
φορές γύρω από τον κύκλο.
Άρα με ισότητα αν και μόνο αν
με ισότητα αν και μόνο αν  για κάθε
για κάθε  , δηλαδή η γωνία
, δηλαδή η γωνία  είναι σε αυτές τις περιπτώσεις πάντα μικρότερη του
είναι σε αυτές τις περιπτώσεις πάντα μικρότερη του  . Αυτό ισχύει π.χ. αν τα σημεία του
. Αυτό ισχύει π.χ. αν τα σημεία του  αποτελούν κορυφές κανονικού πολυγώνου.
αποτελούν κορυφές κανονικού πολυγώνου.
Μπορούμε να υποθέσουμε ότι τα σημεία
 του
του  βρίσκονται πάνω σε κύκλο, έστω ακτίνας
βρίσκονται πάνω σε κύκλο, έστω ακτίνας  . (Γιατί;) Για
. (Γιατί;) Για  ορίζουμε
ορίζουμε  ως το μήκος του τόξου που ξεκινάει από το
ως το μήκος του τόξου που ξεκινάει από το  και καταλήγει στο
και καταλήγει στο  πηγαίνοντας αντιωρολογιακά. Ορίζουμε το
πηγαίνοντας αντιωρολογιακά. Ορίζουμε το  να είναι ίσο με
να είναι ίσο με  αν
αν  και ίσο με
και ίσο με  σε διαφορετική περίπτωση.
σε διαφορετική περίπτωση.Παρατηρούμε ότι
 και για κάθε
και για κάθε  η ποσότητα
η ποσότητα  είναι ίση με
είναι ίση με 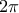 ή
ή  αναλόγως του αν το τρίγωνο
αναλόγως του αν το τρίγωνο  είναι χοντρό ή λεπτό.
είναι χοντρό ή λεπτό.Έτσι έχουμε

Με τους δείκτες modulo
 , για κάθε
, για κάθε  , έχουμε ότι το
, έχουμε ότι το  εμφανίζεται
εμφανίζεται  φορές στο πιο πάνω άθροισμα και άρα το
φορές στο πιο πάνω άθροισμα και άρα το  εμφανίζεται
εμφανίζεται  φορές. Προσθέτοντας αυτά τα δύο έχουμε
φορές. Προσθέτοντας αυτά τα δύο έχουμε  .
.Έτσι έχουμε

Αυτό ισχύει διότι στο
 πάμε
πάμε  φορές γύρω από τον κύκλο.
φορές γύρω από τον κύκλο.Άρα
 με ισότητα αν και μόνο αν
με ισότητα αν και μόνο αν  για κάθε
για κάθε  , δηλαδή η γωνία
, δηλαδή η γωνία  είναι σε αυτές τις περιπτώσεις πάντα μικρότερη του
είναι σε αυτές τις περιπτώσεις πάντα μικρότερη του  . Αυτό ισχύει π.χ. αν τα σημεία του
. Αυτό ισχύει π.χ. αν τα σημεία του  αποτελούν κορυφές κανονικού πολυγώνου.
αποτελούν κορυφές κανονικού πολυγώνου.- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: EGMO 2021
Από περιέργεια, ποια ήταν η δικαιολογία της μη "αποστολής" ελληνικής ομάδας; Να σημειώσουμε ότι το αποστολή είναι παραπλανητικό εδώ, καθώς η ολυμπιάδα έγινε εξ αποστάσεως.Τσιαλας Νικολαος έγραψε: ↑Παρ Απρ 09, 2021 3:24 pmΌπως ανέφερα πρόσφατα η Ελλάδα είναι η μοναδική χώρα που δεν έστειλε εθνική ομάδα παρά τις φιλότιμες προσπάθειες της Ε.Μ.Ε.
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες
