Να αποδειχθεί ότι ο αριθμός
 όπου
όπου  θετικοί ακέραιοι, δεν είναι ποτέ τετράγωνο ακεραίου αριθμού.
θετικοί ακέραιοι, δεν είναι ποτέ τετράγωνο ακεραίου αριθμού.Θέμα 2ο
Για ποιες τιμές του
 έχει το πολυώνυμο
έχει το πολυώνυμο  και τις τρεις ρίζες του ακέραιες;
και τις τρεις ρίζες του ακέραιες;Θέμα 3ο
Αν
 να αποδειχθεί ότι
να αποδειχθεί ότι  . Πότε ισχύει η ισότητα;
. Πότε ισχύει η ισότητα;Θέμα 4ο
Πόσα αθροίσματα
 είναι πολλαπλασια του 3;
είναι πολλαπλασια του 3;Θέμα 5ο
Τρεις κύκλοι με κέντρα
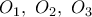 και ακτίνες
και ακτίνες  εφάπτονται ανα δύο εξωτερικώς. Αν
εφάπτονται ανα δύο εξωτερικώς. Αν  είναι η ακτίνα του εγγεγραμμένου κύκλου του τριγώνου
είναι η ακτίνα του εγγεγραμμένου κύκλου του τριγώνου  να αποδειχθεί ότι
να αποδειχθεί ότι  .
.Αλέξανδρος



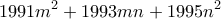 πρέπει να είναι άρτιος. Αυτό, εύκολα βλέπουμε ότι συμβαίνει, μόνο αν οι
πρέπει να είναι άρτιος. Αυτό, εύκολα βλέπουμε ότι συμβαίνει, μόνο αν οι  είναι άρτιοι.
είναι άρτιοι.  με
με 
 και για να είναι τέλειο τετράγωνο, το ίδιο πρέπει να συμβαίνει και με τους
και για να είναι τέλειο τετράγωνο, το ίδιο πρέπει να συμβαίνει και με τους 
 !
!
 οι ακέραιες ρίζες του πολυωνύμου.
οι ακέραιες ρίζες του πολυωνύμου.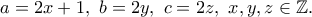

 είναι άρτιοι (αντίκειται στη δεύτερη) ή υπάρχει ακριβώς ένας άρτιος. Αυτό όμως έρχεται σε αντίφαση με τη δεύτερη σχέση.
είναι άρτιοι (αντίκειται στη δεύτερη) ή υπάρχει ακριβώς ένας άρτιος. Αυτό όμως έρχεται σε αντίφαση με τη δεύτερη σχέση.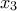 είναι ο αριθμός που θα κάνει το άθροισμα διαιρετό με το 3,όποιοι και να είναι οι άλλοι 2 αριθμοί.Επομένως το
είναι ο αριθμός που θα κάνει το άθροισμα διαιρετό με το 3,όποιοι και να είναι οι άλλοι 2 αριθμοί.Επομένως το 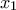 μπορεί να πάρει 300 πιθανές τιμές,το
μπορεί να πάρει 300 πιθανές τιμές,το  επίσης 300 ενώ το
επίσης 300 ενώ το  τέτοια αθροίσματα.
τέτοια αθροίσματα. με τις παρατηρήσεις:
με τις παρατηρήσεις: του τύπου του Ήρωνα είναι τα
του τύπου του Ήρωνα είναι τα 
 , όπου
, όπου  η ημιπερίμετρος του τριγώνου
η ημιπερίμετρος του τριγώνου  .
.
 όπου
όπου  .
. δηλαδή
δηλαδή  απ' όπου έχουμε το ζητούμενο.
απ' όπου έχουμε το ζητούμενο.