 έχουμε
έχουμε 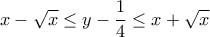 με
με  και
και 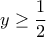 ,
, τότε θα έχουμε και
 .
.2.Θεωρούμε τρίγωνο
 στο οποίο
στο οποίο  κι έστω
κι έστω 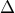 το ίχνος της εσωτερικής διχοτόμους της γωνίας
το ίχνος της εσωτερικής διχοτόμους της γωνίας  με την
με την  .
.α) Να καθοριστεί το διάστημα μεταβολής της γωνίας
 .
.β) Να αποδειχθεί οτι
 και
και  (όπου
(όπου  τα μέτρα των πλευρών του τριγώνου)
τα μέτρα των πλευρών του τριγώνου)3. Έστω η συνάρτηση
 όπου
όπου  και
και  .
.Ν' αποδειχθεί οτι για κάθε
 ισχύει
ισχύει 




 και
και 
 και
και 


 μπορεί εύκολα να γραφεί ότι
μπορεί εύκολα να γραφεί ότι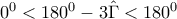

 προκύπτει αμέσως ότι
προκύπτει αμέσως ότι  και έτσι
και έτσι 
 είναι ισοσκελές με
είναι ισοσκελές με  αφού
αφού 

 .
. , τότε είναι λάθος να θέσω
, τότε είναι λάθος να θέσω  και
και  και να δημιουργήσω συνάρτηση έστω
και να δημιουργήσω συνάρτηση έστω ![g(\phi)=\sin^2(b)\sin(\phi)+\cos^2(b)\cos(\phi) , \phi \in [0,\frac{\pi} {2}] g(\phi)=\sin^2(b)\sin(\phi)+\cos^2(b)\cos(\phi) , \phi \in [0,\frac{\pi} {2}]](/forum/ext/geomar/texintegr/latexrender/pictures/c601808762f23f34ef8949a4ed68ac6b.png) ;
; 
 εύκολα προκύπτει ότι
εύκολα προκύπτει ότι  η
η 
 ισχύει ότι :
ισχύει ότι :  για κάθε
για κάθε 
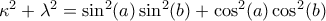 σχέση
σχέση 
 σχέση
σχέση 
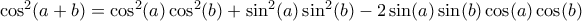 σχέση
σχέση 
 σχέση
σχέση 
 σχέση
σχέση 
 κατά μέλη έχουμε:
κατά μέλη έχουμε:![2=2[\cos^2(a)cos^2(b)+\sin^2(a)\sin^2(b)] + 2[\sin^2(a)\cos^2(b)+\sin^2(b)\cos^2(a)] \Rightarrow 2=2[\cos^2(a)cos^2(b)+\sin^2(a)\sin^2(b)] + 2[\sin^2(a)\cos^2(b)+\sin^2(b)\cos^2(a)] \Rightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/0b6f63fbfb8fa85b5759ce2969363e7b.png)
![\kappa^2+\lambda^2=1-[\sin^2(a)\cos^2(b)+\sin^2(b)\cos^2(a)]\leq1 \kappa^2+\lambda^2=1-[\sin^2(a)\cos^2(b)+\sin^2(b)\cos^2(a)]\leq1](/forum/ext/geomar/texintegr/latexrender/pictures/facf66d07f2e7f5c31976d8a28b6a915.png)
 και συνεπώς
και συνεπώς  για κάθε
για κάθε 




 με
με  δεν είναι λάθος .
δεν είναι λάθος . , οπότε
, οπότε  .
. άρα
άρα  όπου
όπου  η γωνία των δύο διανυσμάτων. Αφού
η γωνία των δύο διανυσμάτων. Αφού  , θα είναι
, θα είναι  .
. .
. ομόσημοι, τότε
ομόσημοι, τότε 
 .
.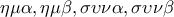 είναι
είναι  , προφανώς ισχύει η ανισότητα.
, προφανώς ισχύει η ανισότητα.