parmenides51 έγραψε:2. Δίνεται επίπεδο

, μια ευθεία του

και ένα σημείο

εκτός του επιπέδου

με απόσταση του από αυτό

.
Έστω

η απόσταση του σημείου

από την ευθεία

.
Από το μέσο

του ευθυγράμμου τμήματος

φέρνουμε την παράλληλο
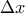
προς την ευθεία

και έστω

τυχαίο σημείο της.
Ζητείται να υπολογισθεί η ελάχιστη απόσταση των ευθειών

και

.
Εργαζόμαστε στο ακόλουθο σχήμα:

- Στερεομετρία 75-76,1.PNG (149.37 KiB) Προβλήθηκε 1832 φορές
Στο σχήμα αυτό έχουμε το επίπεδο

, την ευθεία

πάνω σ' αυτό και ένα σημείο

εκτός αυτού.
Η απόσταση του σημείου

από το επίπεδο

είναι:

Ακόμα η απόσταση του

από την

είναι

Στη συνέχεια θεωρούμε την ευθεία

πάνω στο

η οποία είναι παράλληλη προς την

και
διέρχεται από το μέσο

της

και τέλος πάνω σ' αυτήν ένα τυχαίο σημείο

.
Προφανώς η

τέμνει την

σε ένα σημείο έστω το

για το οποίο ισχύει:

.
Είναι γνωστό ότι η ελάχιστη απόσταση ανάμεσα από τις ασύμβατες ευθείες

και

είναι η κοινή κάθετος αυτών.
Η κοινή κάθετος κατασκευάζεται κατά τα γνωστά.
Από το σημείο

της

φέρουμε κάθετη προς το επίπεδο που ορίζεται από την

και την

. Το επίπεδο αυτό

προφανώς είναι παράλληλο προς την

γιατί

Παρατηρούμε ακόμα ότι το

ανήκει και το επίπεδο που ορίζεται από τις

το

το οποίο είναι κάθετο στην

και στην

(Θεώρημα τριών καθέτων).
Επομένως η κάθετη που ζητάμε είναι η κάθετη από το

προς την

, δηλαδή η

.
(Διότι η  κάθετη στην
κάθετη στην  καθώς και κάθετη στην
καθώς και κάθετη στην  , παράλληλη προς την
, παράλληλη προς την  )
)
Στο σχήμα βλέπουμε τελικά ότι η τελική θέση της κοινής αυτής καθέτου είναι η
 Υπολογισμός της κοινής αυτής καθέτου
Υπολογισμός της κοινής αυτής καθέτου
Το τετράπλευρο

προφανώς είναι εγγράψιμο σε κύκλο και συνεπώς:

και επειδή τα ορθογώνια τρίγωνα

είναι ορθογώνια και ισοσκελή τελικά θα είναι:

η οποία είναι η ζητούμενη ελάχιστη απόστση των ευθειών

.
Κώστας Δόρτσιος
 όπου
όπου  και
και  φυσικός αριθμός.
φυσικός αριθμός. , μια ευθεία του
, μια ευθεία του  και ένα σημείο
και ένα σημείο  εκτός του επιπέδου
εκτός του επιπέδου  με απόσταση του από αυτό
με απόσταση του από αυτό  .
.  η απόσταση του σημείου
η απόσταση του σημείου  από την ευθεία
από την ευθεία  .
.  του ευθυγράμμου τμήματος
του ευθυγράμμου τμήματος  φέρνουμε την παράλληλο
φέρνουμε την παράλληλο 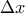 προς την ευθεία
προς την ευθεία  και έστω
και έστω  τυχαίο σημείο της.
τυχαίο σημείο της.  και
και  .
. που επαληθεύουν την εξίσωση
που επαληθεύουν την εξίσωση  .
.
 (1) και
(1) και  (2)
(2) (3) .
(3) . (4)
(4) με
με  για κάθε
για κάθε  . Οπότε
. Οπότε  και επειδή
και επειδή  έχω
έχω  .
.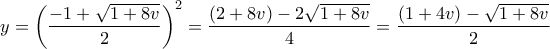
 , την ευθεία
, την ευθεία  πάνω σ' αυτό και ένα σημείο
πάνω σ' αυτό και ένα σημείο 

 πάνω στο
πάνω στο  της
της  και τέλος πάνω σ' αυτήν ένα τυχαίο σημείο
και τέλος πάνω σ' αυτήν ένα τυχαίο σημείο  τέμνει την
τέμνει την  για το οποίο ισχύει:
για το οποίο ισχύει:  .
. είναι η κοινή κάθετος αυτών.
είναι η κοινή κάθετος αυτών.  της
της 

 το
το 
 , δηλαδή η
, δηλαδή η  .
. καθώς και κάθετη στην
καθώς και κάθετη στην  , παράλληλη προς την
, παράλληλη προς την 
 προφανώς είναι εγγράψιμο σε κύκλο και συνεπώς:
προφανώς είναι εγγράψιμο σε κύκλο και συνεπώς: 
 είναι ορθογώνια και ισοσκελή τελικά θα είναι:
είναι ορθογώνια και ισοσκελή τελικά θα είναι:
 .
. το σύστημα έχει λύση την
το σύστημα έχει λύση την 
 π.χ.
π.χ.  .
. ώστε για κάθε
ώστε για κάθε  να αληθεύει το σύστημα;
να αληθεύει το σύστημα;