Δεν έχουν αρνητικούς όρους. Αυτό που κάνει είναι το εξής (θα το κάνω γιαjasonmaths4ever έγραψε:Μπορεί να μην κατάλαβα εγώ καλά, αλλά τι γίνεται αν μια από αυτές τις ακολουθίες έχει έστω και έναν αρνητικό όρο;Al.Koutsouridis έγραψε:Μιας και ο φάκελος είναι για την προετοιμασία παραθέτω την επίσημη λύση για την Άσκηση 7 σε απόκρυψη σε περίπτωση που κάποιος θέλει να ασχοληθεί ακόμα.
 αντί για
αντί για  ).
).Υπάρχουν
 ακολουθίες διαφοράς
ακολουθίες διαφοράς  όπου κάθε
όπου κάθε  ισούται με
ισούται με  ή
ή  ή
ή  . Π.χ. μια ακολουθία διαφοράς είναι η
. Π.χ. μια ακολουθία διαφοράς είναι η  . Αυτή η ακολουθία διαφοράς αντιστοιχεί σε πολλές ακολουθίες που την έχουν ως ακολουθία διαφοράς. Π.χ. στην
. Αυτή η ακολουθία διαφοράς αντιστοιχεί σε πολλές ακολουθίες που την έχουν ως ακολουθία διαφοράς. Π.χ. στην  ή στην
ή στην  κ.τ.λ. Σε όλες αυτές τις ακολουθίες, πάντα ο μικρότερος όρος είναι ο πέμπτος. Υπάρχει λοιπόν μόνο μία ακολουθία που έχει μικρότερο όρο το
κ.τ.λ. Σε όλες αυτές τις ακολουθίες, πάντα ο μικρότερος όρος είναι ο πέμπτος. Υπάρχει λοιπόν μόνο μία ακολουθία που έχει μικρότερο όρο το  και έχει ακολουθία διαφοράς την
και έχει ακολουθία διαφοράς την  . Αυτή είναι η
. Αυτή είναι η  .
. Οπότε υπάρχουν ακριβώς
 ακολουθίες που ο μικρότερός τους όρος είναι ο
ακολουθίες που ο μικρότερός τους όρος είναι ο  . Υπάρχουν άλλες
. Υπάρχουν άλλες  με μικρότερο όρο το
με μικρότερο όρο το  και άλλες
και άλλες  με μικρότερο όρο το
με μικρότερο όρο το  . Συνολικό λοιπόν
. Συνολικό λοιπόν  όπου ο μικρότερος όρος είναι ένας από τους
όπου ο μικρότερος όρος είναι ένας από τους  ή
ή  . Από αυτές μόνο οι
. Από αυτές μόνο οι  δεν έχουν το
δεν έχουν το  ως όρο. Πιο συγκεκριμένα αυτές που όλοι οι όροι τους ισούνται είτε με
ως όρο. Πιο συγκεκριμένα αυτές που όλοι οι όροι τους ισούνται είτε με  είτε με
είτε με  . Οπότε τελικά έχουμε
. Οπότε τελικά έχουμε  ακολουθίες με τις ιδιότητες που θέλουμε.
ακολουθίες με τις ιδιότητες που θέλουμε.
 θεωρούμε την ακολουθία διαφοράς
θεωρούμε την ακολουθία διαφοράς  . Κάθε όρος της ακολουθίας διαφοράς είναι ίσος με 0, 1 ή -1. οπότε το πλήθος όλων των ακολουθιών διαφοράς είναι
. Κάθε όρος της ακολουθίας διαφοράς είναι ίσος με 0, 1 ή -1. οπότε το πλήθος όλων των ακολουθιών διαφοράς είναι  .
. όλων των ενδιαφερουσών ακολουθιών, το ελάχιστο στοιχείο των οποίων δεν υπερβαίνει το 3. Εξετάζουμε μια τυχαία ακολουθία διαφοράς
όλων των ενδιαφερουσών ακολουθιών, το ελάχιστο στοιχείο των οποίων δεν υπερβαίνει το 3. Εξετάζουμε μια τυχαία ακολουθία διαφοράς  . Οποιοισδήποτε δύο ενδιαφέρουσες ακολουθίες που αντιστοιχούν σε αυτήν διαφέρουν στο να αθροίσουμε τον ίδιο αριθμό σε κάθε όρο τους. Άρα μεταξύ αυτών υπάρχει ακριβώς μία ακολουθία με ελάχιστο στοιχείο ίσο με 1, 2 ή 3. Έτσι έχουμε
. Οποιοισδήποτε δύο ενδιαφέρουσες ακολουθίες που αντιστοιχούν σε αυτήν διαφέρουν στο να αθροίσουμε τον ίδιο αριθμό σε κάθε όρο τους. Άρα μεταξύ αυτών υπάρχει ακριβώς μία ακολουθία με ελάχιστο στοιχείο ίσο με 1, 2 ή 3. Έτσι έχουμε  .
. τον αριθμό και το ζητούμενο πλήθος των ακολουθιών είναι
τον αριθμό και το ζητούμενο πλήθος των ακολουθιών είναι  .
. είναι
είναι  .
. , που προκύπτει από το
, που προκύπτει από το  . Όμως το
. Όμως το δίνει γινόμενο
δίνει γινόμενο  που είναι μεγαλύτερο:
που είναι μεγαλύτερο: 


 ένας θετικός ακέραιος. Τοποθετούμε αυθαίρετα στην περιφέρεια ενός κύκλου τους αριθμούς
ένας θετικός ακέραιος. Τοποθετούμε αυθαίρετα στην περιφέρεια ενός κύκλου τους αριθμούς  Σε κάθε χορδή που ενώνει δύο από αυτά τα σημεία αντιστοιχούμε έναν αριθμό που είναι ίσος με την απόλυτη τιμή της διαφοράς των αριθμών σε αυτά τα σημεία.
Σε κάθε χορδή που ενώνει δύο από αυτά τα σημεία αντιστοιχούμε έναν αριθμό που είναι ίσος με την απόλυτη τιμή της διαφοράς των αριθμών σε αυτά τα σημεία. 
 να βρίσκεται στην θέση
να βρίσκεται στην θέση  και το
και το  στην θέση
στην θέση 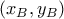 .
.  είναι και οι δύο περιττοί. Δείξτε ότι όποτε μετακινώ το πιόνι
είναι και οι δύο περιττοί. Δείξτε ότι όποτε μετακινώ το πιόνι  πάλι θα είχαμε παράδειγμα με μικρότερη όμως απόσταση μεταξύ των
πάλι θα είχαμε παράδειγμα με μικρότερη όμως απόσταση μεταξύ των  έτσι ώστε
έτσι ώστε  να είναι ταυτόχρονα τέλειοι κύβοι ακεραίων
να είναι ταυτόχρονα τέλειοι κύβοι ακεραίων
 του
του  για τις οποίες ισχύει
για τις οποίες ισχύει  αν ισχύει
αν ισχύει 

 το ζητούμενο πλήθος. Πρώτα αποδεικνύουμε το εξής λήμμα:
το ζητούμενο πλήθος. Πρώτα αποδεικνύουμε το εξής λήμμα: .
. είναι προφανές(
είναι προφανές(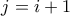 ). Για το
). Για το  έχουμε επαγωγικά:
έχουμε επαγωγικά: , για κάθε
, για κάθε  τέτοιο ώστε να ορίζονται οι δείκτες. Έτσι θέτοντας τώρα
τέτοιο ώστε να ορίζονται οι δείκτες. Έτσι θέτοντας τώρα  έχουμε
έχουμε  , δηλαδή το ζητούμενο.
, δηλαδή το ζητούμενο. του
του 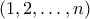 για τις οποίες ισχύει
για τις οποίες ισχύει  . Αυτές τις ονομάζουμε καλές n-άδες. Θα αποδείξουμε επαγωγικά ότι
. Αυτές τις ονομάζουμε καλές n-άδες. Θα αποδείξουμε επαγωγικά ότι  , με
, με  .
. ισχύει. Έστω ισχύει έως το
ισχύει. Έστω ισχύει έως το  . Το δείχνουμε για
. Το δείχνουμε για  και παρατηρούμε ότι κάθε καλή (n-1)-αδα των 1,2,...,n-1 αντιστοιχεί σε μια καλή n-αδα του n και αντίστροφα:
και παρατηρούμε ότι κάθε καλή (n-1)-αδα των 1,2,...,n-1 αντιστοιχεί σε μια καλή n-αδα του n και αντίστροφα: . Άρα για
. Άρα για  επιλογές.
επιλογές. . O
. O  είναι ένας εκ των 1,3,...,n. Άν
είναι ένας εκ των 1,3,...,n. Άν  αριθμός 1 μετά δεν θα μπορεί να μπει σε καμία θέση. Πράγματι έστω
αριθμός 1 μετά δεν θα μπορεί να μπει σε καμία θέση. Πράγματι έστω 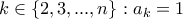 . Τότε από το λήμμα
. Τότε από το λήμμα  , άτοπο αφού
, άτοπο αφού  . Άρα
. Άρα  . Όμοια με πριν έχουμε
. Όμοια με πριν έχουμε  επιλογές λόγω της
επιλογές λόγω της 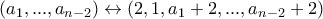 .
. με παρόμοιο σκεπτικό αποδεικνύουμε ότι
με παρόμοιο σκεπτικό αποδεικνύουμε ότι  και άρα έχουμε άλλες
και άρα έχουμε άλλες 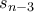 επιλογές.
επιλογές.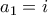 έχουμε
έχουμε  επιλογές καλών n-αδων
επιλογές καλών n-αδων  .
. όπως πριν έχουμε
όπως πριν έχουμε  , άρα 1 επιλογή.
, άρα 1 επιλογή. (το οποιο είναι μικρότερο ή ισο απο
(το οποιο είναι μικρότερο ή ισο απο  ) και έτσι για
) και έτσι για 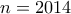 έχουμε τον ζητούμενο αριθμό.
έχουμε τον ζητούμενο αριθμό. .Να βρεθεί το πλήθος των συναρτήσεων
.Να βρεθεί το πλήθος των συναρτήσεων  που είναι επί.
που είναι επί. να υπάρχει
να υπάρχει  ώστε
ώστε 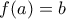 . Τα στοιχεία του Α είναι σε πλήθος ένα παραπάνω από τα στοιχεία του Β. Είναι επομένως φανερό ότι για να είναι η δοσμένη συνάρτηση επί και με σύνολα ορισμού και τιμών τα Α και Β αντίστοιχα, θα πρέπει κάθε ένα στοιχείο του Α να αντιστοιχίζεται σε ένα στοιχείο του Β και κάθε στοιχείο του Β να αντιστοιχίζεται σε ένα στοιχείο του Α, εκτός από ένα που θα αντιστοιχίζεται σε 2. Άρα, αν φανταστούμε τα στοιχεία του Β τοποθετημένα σε
. Τα στοιχεία του Α είναι σε πλήθος ένα παραπάνω από τα στοιχεία του Β. Είναι επομένως φανερό ότι για να είναι η δοσμένη συνάρτηση επί και με σύνολα ορισμού και τιμών τα Α και Β αντίστοιχα, θα πρέπει κάθε ένα στοιχείο του Α να αντιστοιχίζεται σε ένα στοιχείο του Β και κάθε στοιχείο του Β να αντιστοιχίζεται σε ένα στοιχείο του Α, εκτός από ένα που θα αντιστοιχίζεται σε 2. Άρα, αν φανταστούμε τα στοιχεία του Β τοποθετημένα σε  συναρτήσεις.
συναρτήσεις. υπάρχει
υπάρχει  με
με  . Έχουμε πέντε τρόπους να τοποθετήσουμε το
. Έχουμε πέντε τρόπους να τοποθετήσουμε το  τότε για
τότε για  είναι
είναι 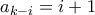 .
.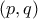 πρώτων αριθμών ώστε
πρώτων αριθμών ώστε 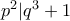 και
και  .
. θετικοί ακέραιοι μικρότεροι του
θετικοί ακέραιοι μικρότεροι του 
 να δείξετε ότι είναι όλοι ίσοι.
να δείξετε ότι είναι όλοι ίσοι.  τότε έχω συνολικά
τότε έχω συνολικά 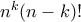 συναρτήσεις, και έτσι αυτές είναι στο σύνολο
συναρτήσεις, και έτσι αυτές είναι στο σύνολο  συναρτήσεις.
συναρτήσεις. 
 ,
,  ,
,  ,
,  συνεπώς τα ζεύγη
συνεπώς τα ζεύγη  αποτελούν λύση οπότε πλέον θα ερευνήσω την εξίσωση για
αποτελούν λύση οπότε πλέον θα ερευνήσω την εξίσωση για 
 Επειδή
Επειδή  τότε ο
τότε ο  θα διαιρεί ακριβώς έναν παράγοντα .
θα διαιρεί ακριβώς έναν παράγοντα . είτε
είτε 
 (1)
(1)
 είτε
είτε  είτε
είτε  είτε
είτε  . Σε κάθε περίπτωση θα ισχύει ότι
. Σε κάθε περίπτωση θα ισχύει ότι  (2)
(2) και τελικά...
και τελικά...
 (3) αλλά από (1)
(3) αλλά από (1)  άρα
άρα q=p+1
q=p+1 αντικαθιστώντας δεν θα έχω λύση για
αντικαθιστώντας δεν θα έχω λύση για  αν και δεν χρειάστηκε .
αν και δεν χρειάστηκε . δεν έχει ακέραιες λύσεις.
δεν έχει ακέραιες λύσεις. ,
,  θετικοί ακέραιοι και
θετικοί ακέραιοι και  τότε
τότε  και
και 
 (γιατί
(γιατί  περιττός)
περιττός)
 τότε από θεώρημα euler θα πρέπει
τότε από θεώρημα euler θα πρέπει  αδύνατον άρα
αδύνατον άρα  άρα
άρα  άρα
άρα  και
και 
 (1) και δεδομένου ότι
(1) και δεδομένου ότι  με προφανή λύση την
με προφανή λύση την  άρα πάω στην (1) συνεπώς
άρα πάω στην (1) συνεπώς 
 (2)
(2)
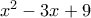 είναι της μορφής
είναι της μορφής  άρα θα έχει πρώτο διαιρέτη της μορφής αυτής αφού αν δεν είχε τότε ως περιττός θα είχε μόνο της μορφής
άρα θα έχει πρώτο διαιρέτη της μορφής αυτής αφού αν δεν είχε τότε ως περιττός θα είχε μόνο της μορφής  που το γινόμενο τους δεν θα ήταν ποτέ της μορφής
που το γινόμενο τους δεν θα ήταν ποτέ της μορφής 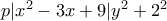 αλλά σύμφωνα με το λήμμα επειδή
αλλά σύμφωνα με το λήμμα επειδή  τότε
τότε  η εύρεση των κατάλληλων
η εύρεση των κατάλληλων