III Φάση (5-6 Φεβρουαρίου 2016) Θέματα 9ης τάξης για την περιφέρεια Μόσχας
Πρώτη μέρα
1. Δίνονται τα δευτεροβάθμια τριώνυμα
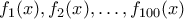 με ίδιο συντελεστή του δευτεροβάθμιου όρου
με ίδιο συντελεστή του δευτεροβάθμιου όρου  , ίδιο συντελεστή του πρωτοβάθμιου όρου
, ίδιο συντελεστή του πρωτοβάθμιου όρου  αλλά διαφορετικό σταθερό όρο. Το καθένα από αυτά έχει δυο ρίζες. Για κάθε τριώνυμο
αλλά διαφορετικό σταθερό όρο. Το καθένα από αυτά έχει δυο ρίζες. Για κάθε τριώνυμο 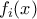 διαλέγουμε μία ρίζα και την συμβολίζουμε με
διαλέγουμε μία ρίζα και την συμβολίζουμε με  . Ποιές τιμές μπορεί να πάρει το άθροισμα
. Ποιές τιμές μπορεί να πάρει το άθροισμα  ;
;2. Δίνεται ισοσκελές τρίγωνο
 ,
,  . Στο περιγεγραμμένο κύκλο
. Στο περιγεγραμμένο κύκλο  του τριγώνου
του τριγώνου  φέρουμε διάμετρο
φέρουμε διάμετρο  . Ευθεία, παράλλη της
. Ευθεία, παράλλη της  που διέρχεται από το
που διέρχεται από το 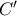 , τέμνει τα τμήματα
, τέμνει τα τμήματα  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα. Να αποδείξετε, ότι το
αντίστοιχα. Να αποδείξετε, ότι το  είναι το μέσο του τμήματος
είναι το μέσο του τμήματος  .
.3. Ο Πέτρος διάλεξε κάποιους διαδοχικούς φυσικούς αριθμούς και έγραψε τον καθένα τους είτε με κόκκινο μολύβι είτε με μπλε(και τα δυο χρώματα είναι παρόντα). Μπορεί το άθροισμα του ελάχιστου κοινού πολλαπλάσιου όλων τον κόκκινων αριθμών και του ελάχιστου κοινού πολλαπλάσιου όλων των μπλε αριθμών να είναι δύναμη του δυο;
4. Ο βασιλιάς Ιέρων έχει 11 μεταλλικές ράβδους, που δε διαφέρουν μεταξύ τους οπτικά. Ο βασιλιάς γνωρίζει ότι με κάποια σειρά οι ράβδοι ζυγίζουν 1,2,…,11 κιλά. Επίσης έχει ένα σάκο που σκίζεται αν περιέχει περισσότερα από 11 κιλά. Ο Αρχιμήδης υπολόγισε τα βάρη των ράβδων και θέλει να αποδείξει στον Ιέρωνα, ότι η πρώτη ράβδος είναι του ενός κιλού. Σε ένα βήμα μπορεί να φορτώσει το σάκο με κάμποσες ράβδους και να επιδείξει στον Ιέρωνα ότι ο σάκος δεν σκίστηκε (δεν επιτρέπεται να σκίσει το σάκο). Ποιος είναι ο ελάχιστος αριθμός φορτώσεων του σάκου που χρειάζεται ο Αρχιμήδης για να επιτύχει το ζητούμενο;
Δεύτερη μέρα
5. Μια τάξη έχει 23 μαθητές. Κατά την διάρκεια του έτους κάθε μαθητής της τάξης από μια φορά γιόρτασε τα γενέθλιά του, στα οποία παρευρέθηκαν κάποιοι συμμαθητές του (τουλάχιστον ένας αλλά όχι όλοι). Μπορεί να προκύψει, ότι κάθε δυο μαθητές αυτής της τάξης συναντήθηκαν στις παραπάνω γιορτές τον ίδιο αριθμό φορές; (θεωρούμε ότι σε κάθε γιορτή συναντήθηκαν οποιοιδήποτε δυο καλεσμένοι καθώς και ο εορτάζων με όλους τους καλεσμένους)
6. Θα ονομάζουμε το μη κενό σύνολο
 (πεπερασμένου ή απειρου πλήθους στοιχείων), που αποτελείται από φυσικούς αριθμούς, πλήρες, αν για οποιουσδήποτε δυο φυσικούς
(πεπερασμένου ή απειρου πλήθους στοιχείων), που αποτελείται από φυσικούς αριθμούς, πλήρες, αν για οποιουσδήποτε δυο φυσικούς  και
και  (όχι απαραίτητα διαφορετικούς και όχι απαραίτητα να ανήκουν στο
(όχι απαραίτητα διαφορετικούς και όχι απαραίτητα να ανήκουν στο  ) τέτοιους ώστε ο
) τέτοιους ώστε ο  να ανήκει στο
να ανήκει στο  , τότε και ο
, τότε και ο  ανήκει στο
ανήκει στο  . Βρείτε όλα τα πλήρη σύνολα φυσικών αριθμών.
. Βρείτε όλα τα πλήρη σύνολα φυσικών αριθμών.7. Σε έναν άσπρο πίνακα διαστάσεων
 κάποια από τα κελιά χρωματίζονται μαύρα. Θα ονομάζουμε ένα φυσικό αριθμό
κάποια από τα κελιά χρωματίζονται μαύρα. Θα ονομάζουμε ένα φυσικό αριθμό  «καλό», αν
«καλό», αν  και σε καθένα από τα τετράγωνα διαστάσεων
και σε καθένα από τα τετράγωνα διαστάσεων 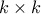 κελιών βρίσκονται ακριβώς
κελιών βρίσκονται ακριβώς  χρωματισμένα κελιά (για παράδειγμα, αν όλα τα κελιά χρωματιστούν μαύρα τότε καλός θα είναι μόνο ο αριθμό 1). Ποιο είναι το μέγιστο πλήθος αριθμών που μπορεί να είναι καλοί;
χρωματισμένα κελιά (για παράδειγμα, αν όλα τα κελιά χρωματιστούν μαύρα τότε καλός θα είναι μόνο ο αριθμό 1). Ποιο είναι το μέγιστο πλήθος αριθμών που μπορεί να είναι καλοί;8. Δίνεται κυρτό τετράπλευρο
 με
με 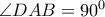 . Έστω
. Έστω  το μέσο της πλευράς
το μέσο της πλευράς  . Αν
. Αν  να αποδείξετε ότι
να αποδείξετε ότι 

 για
για 
 είναι
είναι 

 .
. ο πρόβλημα είναι εξαιρετικά εύκολο ή δεν κατάλαβα καλά. Λοιπόν, δεδομένου ότι σε ένα σύννολο διαδοχικών αριθμών συγκαταλέγονται πάντα και περιττοί, δεν υπάρχει περίπτωση το ελάχιστο κοινό πολλαπλάσιο τους να είναι δύναμη του
ο πρόβλημα είναι εξαιρετικά εύκολο ή δεν κατάλαβα καλά. Λοιπόν, δεδομένου ότι σε ένα σύννολο διαδοχικών αριθμών συγκαταλέγονται πάντα και περιττοί, δεν υπάρχει περίπτωση το ελάχιστο κοινό πολλαπλάσιο τους να είναι δύναμη του  . Όμως αν σαν δύναμη του δύο συμπεριλάβουμε το
. Όμως αν σαν δύναμη του δύο συμπεριλάβουμε το  τους θα είναι ίσο με
τους θα είναι ίσο με  ,
, ,
, ,
, ,
, . Κόκκινοι:
. Κόκκινοι: και επειδή
και επειδή  , το τετράπλευρο
, το τετράπλευρο  είναι ισοσκελές τραπέζιο και άρα
είναι ισοσκελές τραπέζιο και άρα  μεσοκάθετος στο
μεσοκάθετος στο  και
και  και το ζητούμενο έπεται άμεσα.
και το ζητούμενο έπεται άμεσα. οπότε γράφουμε το ημικύκλιο διαμέτρου
οπότε γράφουμε το ημικύκλιο διαμέτρου  και πάνω σε αυτό παίρνουμε σημείο
και πάνω σε αυτό παίρνουμε σημείο  (
(  )
) κατά ίσο τμήμα
κατά ίσο τμήμα  και από το σημείο
και από το σημείο  φέρουμε την
φέρουμε την  και ας είναι
και ας είναι  , οπότε προφανώς
, οπότε προφανώς  (αφού
(αφού  και
και  ) και
) και  (υπό χορδής και εφαπτομένης και εγγεγραμμένη)
(υπό χορδής και εφαπτομένης και εγγεγραμμένη) 
 το τετράπλευρο
το τετράπλευρο  εγγράψιμο σε κύκλο διαμέτρου
εγγράψιμο σε κύκλο διαμέτρου  οπότε
οπότε και το ζητούμενο εδείχθη (με την ...άνωθεν βοήθεια)
και το ζητούμενο εδείχθη (με την ...άνωθεν βοήθεια) με
με  (αφού ο Πέτρος έχει γράψει τουλάχιστον δύο αριθμούς, ένας από αυτούς θα είναι άρτιος).
(αφού ο Πέτρος έχει γράψει τουλάχιστον δύο αριθμούς, ένας από αυτούς θα είναι άρτιος).  Πράγματι, αν
Πράγματι, αν 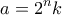 και
και  όπου
όπου 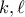 περιττοί με
περιττοί με  τότε ο αριθμός
τότε ο αριθμός 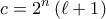 διαιρείται με τον
διαιρείται με τον 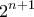 και είναι ανάμεσα σε αυτούς που έγραψε ο Πέτρος, αφού
και είναι ανάμεσα σε αυτούς που έγραψε ο Πέτρος, αφού 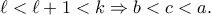 Αυτό, όμως, είναι άτοπο, από την επιλογή του
Αυτό, όμως, είναι άτοπο, από την επιλογή του 
 ) δεν μπορεί να ισούται με δύναμη του
) δεν μπορεί να ισούται με δύναμη του  με βάρη
με βάρη 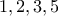 αντίστοιχα. Ο σάκος δεν σκίζεται. (Φυσικά ο Ιέρωνας δεν γνωρίζει ακόμη τα κιλά των ράβδων.)
αντίστοιχα. Ο σάκος δεν σκίζεται. (Φυσικά ο Ιέρωνας δεν γνωρίζει ακόμη τα κιλά των ράβδων.)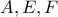 με βάρη
με βάρη 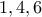 αντίστοιχα. Ο σάκος δεν σκίζεται.
αντίστοιχα. Ο σάκος δεν σκίζεται. αφού σε καμία περίπτωση ο σάκος δεν σκίστηκε.
αφού σε καμία περίπτωση ο σάκος δεν σκίστηκε. .
. και ο Ιέρωνας έχει πειστεί.
και ο Ιέρωνας έχει πειστεί. με
με  , τότε και
, τότε και  . (Παίρνοντας
. (Παίρνοντας  .)
.) για κάποιο φυσικό
για κάποιο φυσικό  ή
ή  .
. με
με  . Πράγματι παίρνοντας
. Πράγματι παίρνοντας 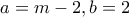 έχουμε
έχουμε  . Όμως
. Όμως  άρα από την προηγούμενη παρατήρηση είναι και
άρα από την προηγούμενη παρατήρηση είναι και  . Παρατηρούμε ότι όλα ικανοποιούν την συνθήκη οπότε τελειώσαμε.
. Παρατηρούμε ότι όλα ικανοποιούν την συνθήκη οπότε τελειώσαμε. ης γραμμής. Παρατηρούμε ότι για κάθε
ης γραμμής. Παρατηρούμε ότι για κάθε 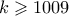 , κάθε
, κάθε  καλούς αριθμούς. Θα δείξουμε ότι δεν μπορούμε να έχουμε περισσότερους καλούς αριθμούς.
καλούς αριθμούς. Θα δείξουμε ότι δεν μπορούμε να έχουμε περισσότερους καλούς αριθμούς.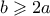 τότε δεν μπορούν οι
τότε δεν μπορούν οι  να είναι και οι δύο καλοί. Το ζητούμενο έπεται κοιτάζοντας τα σύνολα
να είναι και οι δύο καλοί. Το ζητούμενο έπεται κοιτάζοντας τα σύνολα  κάθε ένα εκ των οποίων πρέπει να περιέχει το πολύ έναν καλό αριθμό.
κάθε ένα εκ των οποίων πρέπει να περιέχει το πολύ έναν καλό αριθμό. με
με  . Παίρνουμε ένα
. Παίρνουμε ένα  τετράγωνο. Αυτό το τετράγωνο έχει
τετράγωνο. Αυτό το τετράγωνο έχει  ξένα μεταξύ τους
ξένα μεταξύ τους  τετράγωνα κάθε ένα εκ των οποίων έχει
τετράγωνα κάθε ένα εκ των οποίων έχει  . Τότε όμως έχουμε
. Τότε όμως έχουμε
 . Στα γενέθλια του
. Στα γενέθλια του  πάνε όλοι εκτός από τον
πάνε όλοι εκτός από τον  . (Όπου
. (Όπου 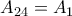 .) Τότε κάθε δύο άτομα συναντιόνται ακριβώς
.) Τότε κάθε δύο άτομα συναντιόνται ακριβώς  φορές.
φορές.