Σχολική φάση(*) για την 9η τάξη.
1. Στην ισότητα
 τοποθετήστε κάμποσα σύμβολα απόλυτης τιμής έτσι, ώστε να γίνει αληθής.
τοποθετήστε κάμποσα σύμβολα απόλυτης τιμής έτσι, ώστε να γίνει αληθής.2. Η Αθηνά και ο Φοίβος έφαγαν μια τούρτα. Η Αθηνά έτρωγε δυο φορές πιο αργά από τον Φοίβο αλλά ξεκίνησε να τρώει ένα λεπτό νωρίτερα. Στο τέλος έφαγαν ίδια ποσότητα τούρτας. Σε πόση ώρα άραγε θα έτρωγε η Αθηνά την τούρτα μόνη της;
3. Ο Δημήτρης σχεδίασε τις γραφικές παραστάσεις τεσσάρων γραμμικών εξισώσεων σε καρτεσιανό σύστημα συντεταγμένων αλλά ξέχασε να σημειώσει τα μοναδιαία διαστήματα. Όταν αντέγραφε την άσκηση στο «καθαρό» τετράδιο, αποσπάστηκε η προσοχή του και δεν έγραψε ολόκληρες τις εξισώσεις με αριθμό 3 και 4. Να βρείτε αυτές τις εξισώσεις. Εξηγήστε την απάντησή σας.
4. Τρεις μαθητές διατύπωσαν από δυο προτάσεις για τους φυσικούς αριθμούς
 .
. Αντώνης: 1)
 = 34 2)
= 34 2)  =56
=56Παύλος: 1)
 2) ο μικρότερος από τους αριθμούς είναι ο 5
2) ο μικρότερος από τους αριθμούς είναι ο 5Μαρία: 1)
 2) Οι
2) Οι  είναι πρώτοι
είναι πρώτοιΤου κάθε μαθητή η μια πρόταση είναι αληθής και η άλλη ψευδής. Να βρείτε τους αριθμούς
 .
.5. Στο ισόπλευρο τρίγωνο
 πλευράς
πλευράς  τα σημεία
τα σημεία  είναι τοποθετημένα όπως στο σχήμα. Αν
είναι τοποθετημένα όπως στο σχήμα. Αν  , να βρείτε το μέγεθος της γωνίας
, να βρείτε το μέγεθος της γωνίας  .
.6. Σε μια σκακιέρα είναι τοποθετημένοι 21 βασιλείς. Ο καθένας από τους οποίους βρίσκεται υπό την απειλή κάποιου άλλου. Μετά την αφαίρεση μερικών από αυτών, κανένας βασιλιάς δεν απειλεί κάποιον άλλων. Ποιος μπορεί να είναι ο μέγιστος αριθμός των βασιλιάδων που απέμειναν.
α) Φέρτε παράδειγμα μιας τέτοιας αρχικής τοποθέτησης καθώς και τις θέσεις των βασιλιάδων που αφαιρέθηκαν.
β) Αποδείξτε, ότι μεγαλύτερος αριθμός βασιλιάδων δεν μπορεί να παραμείνουν στην σκακιέρα.
(*) Ο διαγωνισμός αυτός είναι η πρώτη φάση της ολυμπιάδας και γίνεται σε επίπεδο σχολείου.

 που δεν είναι δυνατόν, ενώ αν
που δεν είναι δυνατόν, ενώ αν ![abc=56 \Leftrightarrow a=\sqrt[3]{56} abc=56 \Leftrightarrow a=\sqrt[3]{56}](/forum/ext/geomar/texintegr/latexrender/pictures/0334a54916352b44578fb667cd59cc22.png) , πάλι αδύνατον.
, πάλι αδύνατον. , αφού οι
, αφού οι  , έστω ο
, έστω ο  . Από αυτά που είπε ο Παύλος, αφού έχουμε ήδη έναν αριθμό
. Από αυτά που είπε ο Παύλος, αφού έχουμε ήδη έναν αριθμό  ,
,  , και φυσικά όλες οι μεταθέσεις αυτής της τριάδας.
, και φυσικά όλες οι μεταθέσεις αυτής της τριάδας. , πρέπει
, πρέπει 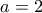 ή
ή  ή
ή  .
. , οπότε
, οπότε  , που δεν είναι πρώτος.
, που δεν είναι πρώτος. , και όλες οι μεταθέσεις.
, και όλες οι μεταθέσεις.
 ,
,  ) , από όπου προκύπτει
) , από όπου προκύπτει 
 είναι η μόνη που διέρχεται από την αρχή των αξόνων θα έχει εξίσωση
είναι η μόνη που διέρχεται από την αρχή των αξόνων θα έχει εξίσωση  Εξάλλου η
Εξάλλου η  είναι η μόνη
είναι η μόνη Αν η
Αν η  έχει συντελεστή διεύθυνσης
έχει συντελεστή διεύθυνσης  τότε επειδή
τότε επειδή  θα έχει εξίσωση
θα έχει εξίσωση  . Τότε όμως θα τέμνει την
. Τότε όμως θα τέμνει την  ,
,  έχει συντελεστή διεύθυνσης
έχει συντελεστή διεύθυνσης  θα έχει εξίσωση
θα έχει εξίσωση  και θα τέμνει την
και θα τέμνει την  .
. 
 κι επειδή
κι επειδή  , τα τρίγωνα
, τα τρίγωνα 
 , άρα το
, άρα το  είναι εγγράψιμο και κατά συνέπεια
είναι εγγράψιμο και κατά συνέπεια 
 μαύρους βασιλιάδες και να μείνουν οι
μαύρους βασιλιάδες και να μείνουν οι 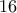 άσπροι.
άσπροι. βασιλιάδες. Δηλαδή αφαιρέσαμε το πολύ
βασιλιάδες. Δηλαδή αφαιρέσαμε το πολύ  βασιλιάδες. Για κάθε βασιλιά που απέμεινε υπάρχει τουλάχιστον ένας βασιλιάς που αφαιρέθηκε ο οποίος τον απειλούσε. Εφόσον όμως έμειναν τουλάχιστον
βασιλιάδες. Για κάθε βασιλιά που απέμεινε υπάρχει τουλάχιστον ένας βασιλιάς που αφαιρέθηκε ο οποίος τον απειλούσε. Εφόσον όμως έμειναν τουλάχιστον  τετράγωνα τα οποία μπορούμε να τα χωρίσουμε σε ζεύγη τα οποία απειλούνται μεταξύ τους. Οπότε σε κάθε τέτοιο ζεύγος υπάρχει το πολύ ένας βασιλιάς ο οποίος παρέμεινε. Άρα κάθε βασιλιάς που αφαιρέθηκε απειλεί το πολύ
τετράγωνα τα οποία μπορούμε να τα χωρίσουμε σε ζεύγη τα οποία απειλούνται μεταξύ τους. Οπότε σε κάθε τέτοιο ζεύγος υπάρχει το πολύ ένας βασιλιάς ο οποίος παρέμεινε. Άρα κάθε βασιλιάς που αφαιρέθηκε απειλεί το πολύ  , τότε η
, τότε η