Α' Λυκείου
Πρόβλημα 1
(α) Να αποδείξετε ότι για κάθε πραγματικό αριθμό
 ισχύει η ανισότητα:
ισχύει η ανισότητα: 
(β) Να αποδείξετε ότι για κάθε θετικό ακέραιο αριθμό
 η προηγούμενη ανισότητα γίνεται:
η προηγούμενη ανισότητα γίνεται: 
(γ) Να αποδείξετε ότι ισχύει:

Πρόβλημα 2
(α) Να γράψετε την παράσταση
 ως γινόμενο δύο τριωνύμων της μορφής
ως γινόμενο δύο τριωνύμων της μορφής  .
.(β) Να αποδείξετε ότι για κάθε θετικό ακέραιο
 ο θετικός ακέραιος αριθμός
ο θετικός ακέραιος αριθμός  δεν είναι ποτέ πρώτος.
δεν είναι ποτέ πρώτος.Πρόβλημα 3
Από τις κορυφές
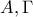 ορθογωνίου
ορθογωνίου  με
με  φέρουμε τις κάθετες
φέρουμε τις κάθετες  στη διαγώνιο
στη διαγώνιο  (
( σημεία της διαγωνίου
σημεία της διαγωνίου  ). Με πλευρές τις
). Με πλευρές τις  και
και  κατασκευάζουμε τα ισόπλευρα τρίγωνα
κατασκευάζουμε τα ισόπλευρα τρίγωνα  και
και  που βρίσκονται εκτός του ορθογωνίου
που βρίσκονται εκτός του ορθογωνίου  . Να αποδείξετε ότι:
. Να αποδείξετε ότι:(α) το
 είναι παραλληλόγραμμο
είναι παραλληλόγραμμο(β) η
 περνά από το κέντρο του
περνά από το κέντρο του 
(γ) η
 είναι παράλληλη προς τις
είναι παράλληλη προς τις 
Πρόβλημα 4
Να λύσετε το σύστημα:



 πρώτος θα πρέπει
πρώτος θα πρέπει  (αφού
(αφού  ),
), 
 , άρα το
, άρα το 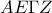 είναι παραλληλόγραμμο, οπότε οι
είναι παραλληλόγραμμο, οπότε οι  διχοτομούνται.
διχοτομούνται. , προκύπτει ότι
, προκύπτει ότι  , οπότε και το
, οπότε και το  είναι
είναι  διχοτομούνται. Επομένως οι
διχοτομούνται. Επομένως οι  διχοτομούνται, άρα το το
διχοτομούνται, άρα το το  , που είναι το κέντρο του ορθογωνίου.
, που είναι το κέντρο του ορθογωνίου. ισοσκελή, άρα η
ισοσκελή, άρα η  είναι μεσοκάθετη των
είναι μεσοκάθετη των ,
,  .
. έχουμε ισοδύναμα
έχουμε ισοδύναμα  οπότε
οπότε  άρα και
άρα και  .
.
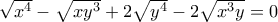
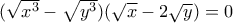 , δηλαδή
, δηλαδή  ή
ή  .
.  προκύπτει μοναδική λύση
προκύπτει μοναδική λύση  .
. είναι προφανώς μη μηδενικά. Συνεπώς διαιρώντας την πρώτη με
είναι προφανώς μη μηδενικά. Συνεπώς διαιρώντας την πρώτη με  και τη δεύτερη με
και τη δεύτερη με  παίρνουμε το ισοδύναμο σύστημα
παίρνουμε το ισοδύναμο σύστημα 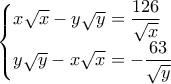
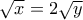 δηλαδή ισοδύναμα (αφού
δηλαδή ισοδύναμα (αφού 
 στην αρχική , οπότε:
στην αρχική , οπότε: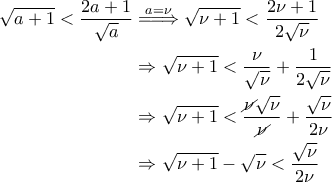


 είναι θετικός ακέραιος, να αποδείξετε ότι:
είναι θετικός ακέραιος, να αποδείξετε ότι: 
 φέρουμε το ύψος
φέρουμε το ύψος  διαμέτρου
διαμέτρου  τέμνει τις πλευρές
τέμνει τις πλευρές  στα σημεία
στα σημεία  αντίστοιχα. Η διχοτόμος της γωνίας
αντίστοιχα. Η διχοτόμος της γωνίας  τέμνει την πλευρά
τέμνει την πλευρά  στο σημείο
στο σημείο 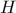 και η διχοτόμος της γωνίας
και η διχοτόμος της γωνίας  τέμνει τον κύκλο
τέμνει τον κύκλο  στο σημείο
στο σημείο 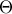 . Να αποδείξετε ότι:
. Να αποδείξετε ότι: είναι όμοια
είναι όμοια
 να αποδείξετε ότι (με
να αποδείξετε ότι (με  συμβολίζουμε το εμβαδόν του
συμβολίζουμε το εμβαδόν του 
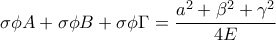
 είναι εσωτερικό σημείο του
είναι εσωτερικό σημείο του  να αποδείξετε ότι:
να αποδείξετε ότι: 
 (εγγεγραμμένες στο ίδιο τόξο). Το τρίγωνο
(εγγεγραμμένες στο ίδιο τόξο). Το τρίγωνο  είναι ορθογώνιο και το
είναι ορθογώνιο και το  είναι ύψος,
είναι ύψος,  , άρα τα ζητούμενα τρίγωνα είναι όμοια.
, άρα τα ζητούμενα τρίγωνα είναι όμοια. , αλλά λόγω της διχοτόμου,
, αλλά λόγω της διχοτόμου, 




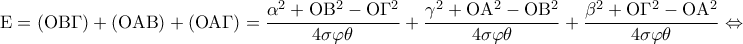


 , αφού
, αφού  (επειδή
(επειδή  και
και  )
)

 . Θα αποδείξουμε ότι ισχύει και για τον
. Θα αποδείξουμε ότι ισχύει και για τον  . Αφού ισχυέι η
. Αφού ισχυέι η  Πρέπει λοιπόν να αποδείξουμε ότι:
Πρέπει λοιπόν να αποδείξουμε ότι: ή
ή  ή
ή  ή
ή  το οποίο είναι προφανές.
το οποίο είναι προφανές. 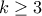 τότε ισχύει και για τον
τότε ισχύει και για τον 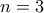 , έπεται ότι ισχύει για όλους τους θετικούς
, έπεται ότι ισχύει για όλους τους θετικούς  .
. και
και  ενός ορθοκανονικού συστήματος αξόνων παίρνουμε, αντίστοιχα, τα σημεία
ενός ορθοκανονικού συστήματος αξόνων παίρνουμε, αντίστοιχα, τα σημεία 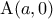 και
και  . Έστω επίσης
. Έστω επίσης  δύο τυχαία σημεία του ημιάξονα
δύο τυχαία σημεία του ημιάξονα  . Από το σημείο
. Από το σημείο  φέρουμε παράλληλες προς τις ευθείες
φέρουμε παράλληλες προς τις ευθείες  οι οποίες τέμνουν τον άξονα
οι οποίες τέμνουν τον άξονα  αντίστοιχα. Αν
αντίστοιχα. Αν  είναι το σημείο τομής των ευθειών
είναι το σημείο τομής των ευθειών  και
και  είναι το σημείο τομής των ευθειών
είναι το σημείο τομής των ευθειών  να αποδείξετε ότι:
να αποδείξετε ότι: είναι παραλληλόγραμμο
είναι παραλληλόγραμμο , όπου
, όπου  είναι τα εμβαδά των τριγώνων
είναι τα εμβαδά των τριγώνων  , αντίστοιχα.
, αντίστοιχα.  με τύπο
με τύπο  .
. , ώστε να ισχύει:
, ώστε να ισχύει: 
 με τύπο
με τύπο 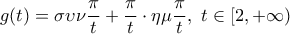 ως προς τη μονοτονία και τα ακρότατα.
ως προς τη μονοτονία και τα ακρότατα. και να αποδείξετε ότι:
και να αποδείξετε ότι: 
 και
και  από το Θ. του Θαλή προκύπτουν:
από το Θ. του Θαλή προκύπτουν:  και
και  .
. , οπότε
, οπότε  και έτσι το τετράπλευρο
και έτσι το τετράπλευρο  είναι όμοια και ισχύει:
είναι όμοια και ισχύει:  .
. .
.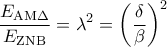 .
.