Σελίδα 1 από 1
Τεστ Εξάσκησης #1-ΑΡΧΙΜΗΔΗΣ
Δημοσιεύτηκε: Παρ Φεβ 24, 2017 8:04 pm
από achilleas
Καλησπέρα σας!
Την περίοδο πριν τον ΑΡΧΙΜΗΔΗ πέρυσι, είχα ετοιμάσει κάποια τεστ προετοιμασίας για τον μαθητή του σχολείου μας Νικόλαο Ευγενίδη.
Οι κανόνες ήταν να γράψει το τεστ στο σπίτι του υπό διαγωνιστικές συνθήκες, σε 4 ώρες. Στη συνέχεια συζητούσαμε τις λύσεις τους στο σχολείο.
Παρεμπιπτόντως, ο Νίκος προκρίθηκε και φέτος για 4η συνεχή χρονιά.
Ελπίζω κάποια από αυτά να φανούν χρήσιμα και φέτος σε όποιον θέλει κάποια εξάσκηση.
**********************************************
Ακολουθούν τα προβλήματα του 1ου τεστ:
Practice TEST 1
ΔΙΑΡΚΕΙΑ: 4 ΩΡΕΣ
ΘΕΜΑ 1. Να βρεθούν όλα τα πολυώνυμα

και

με πραγματικούς συντελεστές τέτοια ώστε

και

για κάθε πραγματικό

.
ΘΕΜΑ 2. Να βρεθούν όλοι οι θετικοί ακέραιοι

τέτοιοι ώστε οι αριθμοί

και

να είναι πρώτοι και να ισχύει
 ΘΕΜΑ 3.
ΘΕΜΑ 3. Να δειχθεί ότι αν

, τότε
 ΘΕΜΑ 4.
ΘΕΜΑ 4. Δίνεται κυρτό πεντάγωνο

τέτοιο ώστε

και

και

Να αποδειχθεί ότι το τετράπλευρο

είναι παραλληλόγραμμο.
**********************************************
Φιλικά,
Αχιλλέας
Re: Τεστ Εξάσκησης #1-ΑΡΧΙΜΗΔΗΣ
Δημοσιεύτηκε: Παρ Φεβ 24, 2017 8:08 pm
από harrisp
Κύριε Αχιλλέα ειναι τελειο. Μήπως εχετε και για JUNIORS;;;
Θα ήμουν ευγνώμων....
Re: Τεστ Εξάσκησης #1-ΑΡΧΙΜΗΔΗΣ
Δημοσιεύτηκε: Παρ Φεβ 24, 2017 11:08 pm
από achilleas
ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Κύριε Αχιλλέα ειναι τελειο. Μήπως εχετε και για JUNIORS;;;
Θα ήμουν ευγνώμων....
Καλησπέρα, Χάρη,
Δυστυχώς δεν έχω ετοιμάσει κάτι σε Juniors, αλλά ελπίζω να βρω χρόνο να το κάνω σύντομα.
Παρεμπιπτόντως, το παραπάνω 1ο τεστ αποδείχθηκε στην πράξη ότι ήταν αρκετά δύσκολο.
Έτσι, προσπάθησα στα επόμενα τεστ να έχω και μια πιο προσιτή άσκηση, τουλάχιστον σε όποιο μαθητή έχει ασχοληθεί με διαγωνισμούς.
Δεν ισχυρίζομαι, λοιπόν, ότι το επίπεδο δυσκολίας ταυτίζεται με αυτό του ΑΡΧΙΜΗΔΗ. Ελπίζω να είναι κοντά, πάντως.
Φιλικά,
Αχιλλέας
Re: Τεστ Εξάσκησης #1-ΑΡΧΙΜΗΔΗΣ
Δημοσιεύτηκε: Παρ Φεβ 24, 2017 11:22 pm
από matha
achilleas έγραψε:
ΘΕΜΑ 3. Να δειχθεί ότι αν

, τότε

Υποθέτουμε ότι

οπότε είναι

και είναι

οπότε αρκεί
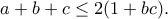
Επειδή είναι

άρα

αρκεί να αποδειχθεί ότι
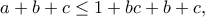
η οποία προφανώς ισχύει.
Re: Τεστ Εξάσκησης #1-ΑΡΧΙΜΗΔΗΣ
Δημοσιεύτηκε: Σάβ Φεβ 25, 2017 1:05 pm
από dement
Διαφορετικά για το 3:
Το αριστερό μέλος είναι κυρτή συνάρτηση της κάθε μεταβλητής, οπότε μεγιστοποιείται σε κάποιο άκρο. Εξετάζοντας περιπτώσεις βλέπουμε ότι το ολικό μέγιστο επιτυγχάνεται για

με τιμή

.
Re: Τεστ Εξάσκησης #1-ΑΡΧΙΜΗΔΗΣ
Δημοσιεύτηκε: Σάβ Φεβ 25, 2017 5:05 pm
από emouroukos
achilleas έγραψε:
Practice TEST 1
ΔΙΑΡΚΕΙΑ: 4 ΩΡΕΣ
ΘΕΜΑ 2. Να βρεθούν όλοι οι θετικοί ακέραιοι

τέτοιοι ώστε οι αριθμοί

και

να είναι πρώτοι και να ισχύει

Δίχως βλάβη της γενικότητας, υποθέτουμε ότι

Παρατηρούμε ότι:

οπότε

Αλλά είναι:

κι αφού ο αριθμός

είναι πρώτος, θα πρέπει να διαρεί τον

ή τον
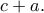
Επειδή

ο

δεν μπορεί να διαιρεί τον

Άρα, θα διαιρεί τον

οπότε θα υπάρχει θετικός ακέραιος

τέτοιος, ώστε
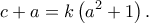
Αλλά έχουμε ότι:

οπότε

και άρα

και

Εύκολα τώρα βρίσκουμε ότι

Λόγω συμμετρίας, προκύπτει και η λύση

Re: Τεστ Εξάσκησης #1-ΑΡΧΙΜΗΔΗΣ
Δημοσιεύτηκε: Σάβ Φεβ 25, 2017 5:48 pm
από emouroukos
achilleas έγραψε:
ΘΕΜΑ 1. Να βρεθούν όλα τα πολυώνυμα

και

με πραγματικούς συντελεστές τέτοια ώστε

και

για κάθε πραγματικό

.
Από τις σχέσεις

και

προκύπτει ότι:

![\displaystyle{ \Rightarrow 4x = \left[ {Q\left( { - x} \right) - Q\left( x \right)} \right]\left[ {Q\left( { - x} \right) + Q\left( x \right)} \right]} \displaystyle{ \Rightarrow 4x = \left[ {Q\left( { - x} \right) - Q\left( x \right)} \right]\left[ {Q\left( { - x} \right) + Q\left( x \right)} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/ee9324837dfd57ed4ede523c3ffc0958.png)

.
Επειδή το πολυώνυμο

περιέχει μόνο άρτιες δυνάμεις του

, ενώ το πολυώνυμο

περιέχει μόνο περιττές δυνάμεις του

, η σχέση

δίνει ότι το πολυώνυμο

είναι σταθερό (μη μηδενικό), και το πολυώνυμο

έχει βαθμό

, με σταθερό όρο ίσο με

(αφού έχει ρίζα το

). Επομένως, υπάρχουν αριθμοί

με

τέτοιοι, ώστε

και

από όπου άμεσα προκύπτει ότι

Από τη σχέση

έχουμε ότι το πολυώνυμο

έχει βαθμό

, οπότε θα υπάρχουν

με

τέτοιοι, ώστε

Έχουμε ότι:

οπότε


και

Έτσι, είναι
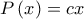
και

Η σχέση

δίνει τώρα ότι:

οπότε
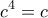
και άρα
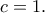
Ώστε, είναι

και
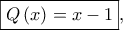
που, όπως εύκολα ελέγχουμε, επαληθεύουν τις δοσμένες σχέσεις.
Re: Τεστ Εξάσκησης #1-ΑΡΧΙΜΗΔΗΣ
Δημοσιεύτηκε: Κυρ Φεβ 26, 2017 9:36 pm
από Demetres
achilleas έγραψε:
ΘΕΜΑ 2. Να βρεθούν όλοι οι θετικοί ακέραιοι

τέτοιοι ώστε οι αριθμοί

και

να είναι πρώτοι και να ισχύει

Δίνω μια διαφορετική απόδειξη η οποία βασίζεται στο πλήθος των τρόπων που μπορούμε να γράψουμε έναν φυσικό αριθμό ως άθροισμα δύο τετραγώνων.
Αν

σε γινόμενο πρώτων παραγόντων όπου

και

, τότε ο

γράφεται ως άθροισμα δύο τετραγώνων αν και μόνο αν όλα τα

είναι άρτιοι. Επιπλέον σε αυτήν την περίπτωση αυτό μπορεί να γίνει με ακριβώς

τρόπους αν όλα τα

είναι άρτιοι

τρόπους αν τουλάχιστον ένα

είναι περιττος
Στην καταμέτρηση δεν λαμβάνονται υπόψη ούτε τα πρόσημα ούτε και η σειρά.
Στην άσκησή μας τώρα:
Έστω χωρίς βλάβη της γενικότητας ότι

. Το
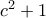
είναι γινόμενο δυο πρώτων της μορφής

ή

. Από τα προηγούμενα το
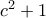
μπορεί να γραφεί ως άθροισμα δύο τετραγώνων με
- έναν τρόπο αν

ή αν

- δύο τρόπους σε διαφορετική περίπτωση
Αλλά
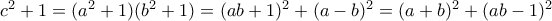
. Αφού
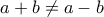
τότε αυτοί είναι δύο διαφορετικοί τρόποι εκτός και αν
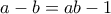
και

το οποίο δίνει

.
Άρα σε κάθε περίπτωση πρέπει ένα από τα

να ισούται με

. Επειδή

πρέπει

. (Η περίπτωση
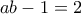
επίσης δίνει

.) Τότε όμως ένας από τους

και

είναι άρτιος και άρα ισούται με το

. Οπότε

και
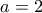
το οποίο ελέγχουμε ότι είναι δεκτό.
Re: Τεστ Εξάσκησης #1-ΑΡΧΙΜΗΔΗΣ
Δημοσιεύτηκε: Τρί Μαρ 10, 2020 3:46 pm
από socrates
achilleas έγραψε: ↑Παρ Φεβ 24, 2017 8:04 pm
ΘΕΜΑ 4. Δίνεται κυρτό πεντάγωνο

τέτοιο ώστε

και

και

Να αποδειχθεί ότι το τετράπλευρο

είναι παραλληλόγραμμο.
Επαναφορά!
Re: Τεστ Εξάσκησης #1-ΑΡΧΙΜΗΔΗΣ
Δημοσιεύτηκε: Τρί Μαρ 10, 2020 4:58 pm
από min##
4.
Έστω

σημείο ώστε

(όμοια με ίδιο προσανατολισμό).
Τότε είναι

και

από υπόθεση.
Έτσι το

είναι το ορθόκεντρο του
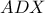
.
Έχουμε :

.
και επιπλέον από κατασκευή,
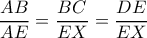
.
Έτσι

.
Από την ομοιότητα τώρα,

,που λόγω

δίνει

.
 και
και  με πραγματικούς συντελεστές τέτοια ώστε
με πραγματικούς συντελεστές τέτοια ώστε  και
και 
 .
. τέτοιοι ώστε οι αριθμοί
τέτοιοι ώστε οι αριθμοί  και
και  να είναι πρώτοι και να ισχύει
να είναι πρώτοι και να ισχύει
 , τότε
, τότε 
 τέτοιο ώστε
τέτοιο ώστε  και
και και
και 
 είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. και
και  με πραγματικούς συντελεστές τέτοια ώστε
με πραγματικούς συντελεστές τέτοια ώστε  και
και 
 .
. τέτοιοι ώστε οι αριθμοί
τέτοιοι ώστε οι αριθμοί  και
και  να είναι πρώτοι και να ισχύει
να είναι πρώτοι και να ισχύει
 , τότε
, τότε 
 τέτοιο ώστε
τέτοιο ώστε  και
και και
και 
 είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. οπότε είναι
οπότε είναι  και είναι
και είναι
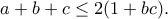
 άρα
άρα  αρκεί να αποδειχθεί ότι
αρκεί να αποδειχθεί ότι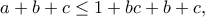 η οποία προφανώς ισχύει.
η οποία προφανώς ισχύει. με τιμή
με τιμή  .
. Παρατηρούμε ότι:
Παρατηρούμε ότι:


 είναι πρώτος, θα πρέπει να διαρεί τον
είναι πρώτος, θα πρέπει να διαρεί τον  ή τον
ή τον 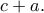
 ο
ο  Άρα, θα διαιρεί τον
Άρα, θα διαιρεί τον  οπότε θα υπάρχει θετικός ακέραιος
οπότε θα υπάρχει θετικός ακέραιος  τέτοιος, ώστε
τέτοιος, ώστε 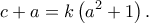 Αλλά έχουμε ότι:
Αλλά έχουμε ότι:
 και άρα
και άρα  και
και  Εύκολα τώρα βρίσκουμε ότι
Εύκολα τώρα βρίσκουμε ότι  Λόγω συμμετρίας, προκύπτει και η λύση
Λόγω συμμετρίας, προκύπτει και η λύση 



![\displaystyle{ \Rightarrow 4x = \left[ {Q\left( { - x} \right) - Q\left( x \right)} \right]\left[ {Q\left( { - x} \right) + Q\left( x \right)} \right]} \displaystyle{ \Rightarrow 4x = \left[ {Q\left( { - x} \right) - Q\left( x \right)} \right]\left[ {Q\left( { - x} \right) + Q\left( x \right)} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/ee9324837dfd57ed4ede523c3ffc0958.png)
 .
. περιέχει μόνο άρτιες δυνάμεις του
περιέχει μόνο άρτιες δυνάμεις του  περιέχει μόνο περιττές δυνάμεις του
περιέχει μόνο περιττές δυνάμεις του  , με σταθερό όρο ίσο με
, με σταθερό όρο ίσο με  (αφού έχει ρίζα το
(αφού έχει ρίζα το  με
με  τέτοιοι, ώστε
τέτοιοι, ώστε 



 έχει βαθμό
έχει βαθμό  με
με  τέτοιοι, ώστε
τέτοιοι, ώστε 


 και
και  Έτσι, είναι
Έτσι, είναι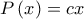


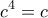 και άρα
και άρα 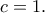
 και
και 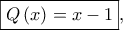 που, όπως εύκολα ελέγχουμε, επαληθεύουν τις δοσμένες σχέσεις.
που, όπως εύκολα ελέγχουμε, επαληθεύουν τις δοσμένες σχέσεις. σε γινόμενο πρώτων παραγόντων όπου
σε γινόμενο πρώτων παραγόντων όπου  και
και  , τότε ο
, τότε ο  γράφεται ως άθροισμα δύο τετραγώνων αν και μόνο αν όλα τα
γράφεται ως άθροισμα δύο τετραγώνων αν και μόνο αν όλα τα  είναι άρτιοι. Επιπλέον σε αυτήν την περίπτωση αυτό μπορεί να γίνει με ακριβώς
είναι άρτιοι. Επιπλέον σε αυτήν την περίπτωση αυτό μπορεί να γίνει με ακριβώς  τρόπους αν όλα τα
τρόπους αν όλα τα  είναι άρτιοι
είναι άρτιοι τρόπους αν τουλάχιστον ένα
τρόπους αν τουλάχιστον ένα  . Το
. Το 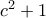 είναι γινόμενο δυο πρώτων της μορφής
είναι γινόμενο δυο πρώτων της μορφής  ή
ή  . Από τα προηγούμενα το
. Από τα προηγούμενα το  ή αν
ή αν 
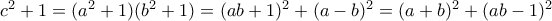 . Αφού
. Αφού 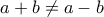 τότε αυτοί είναι δύο διαφορετικοί τρόποι εκτός και αν
τότε αυτοί είναι δύο διαφορετικοί τρόποι εκτός και αν 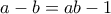 και
και  το οποίο δίνει
το οποίο δίνει  να ισούται με
να ισούται με  πρέπει
πρέπει  . (Η περίπτωση
. (Η περίπτωση 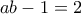 επίσης δίνει
επίσης δίνει 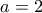 το οποίο ελέγχουμε ότι είναι δεκτό.
το οποίο ελέγχουμε ότι είναι δεκτό. σημείο ώστε
σημείο ώστε  (όμοια με ίδιο προσανατολισμό).
(όμοια με ίδιο προσανατολισμό). και
και  από υπόθεση.
από υπόθεση. είναι το ορθόκεντρο του
είναι το ορθόκεντρο του 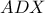 .
. .
.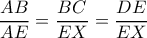 .
. .
. ,που λόγω
,που λόγω  .
.