Σε συνέχεια των προηγούμενων θεμάτων με το 1ο τεστ και το 2ο τεστ, ακολουθούν τα προβλήματα του 3ου τεστ:
**********************************************
Practice TEST 3
ΔΙΑΡΚΕΙΑ: 4 ΩΡΕΣ
ΘΕΜΑ 1. Έστω
 θετικός ακέραιος. Αν οι
θετικός ακέραιος. Αν οι  είναι θετικοί πραγματικοί αριθμοί τέτοιοι ώστε
είναι θετικοί πραγματικοί αριθμοί τέτοιοι ώστε  , τότε να δειχθεί ότι
, τότε να δειχθεί ότι
ΘΕΜΑ 2. Έστω
 ένα κυρτό τετράπλευρο και έστω
ένα κυρτό τετράπλευρο και έστω  ένα σημείο στην πλευρά
ένα σημείο στην πλευρά  τέτοιο ώστε
τέτοιο ώστε  Εάν
Εάν  είναι το σημείο τομής της ευθείας
είναι το σημείο τομής της ευθείας  με τη μεσοκάθετο του τμήματος
με τη μεσοκάθετο του τμήματος  , να δειχθεί ότι
, να δειχθεί ότι 
ΘΕΜΑ 3. Να δειχθεί ότι δεν υπάρχουν θετικοί ακέραιοι
 τέτοιοι ώστε
τέτοιοι ώστε
ΘΕΜΑ 4. Να βρεθεί ο μεγαλύτερος θετικός ακέραιος
 για τον οποίο υπάρχει ένα σύνολο
για τον οποίο υπάρχει ένα σύνολο  με ακριβώς
με ακριβώς  στοιχεία τέτοια ώστε
στοιχεία τέτοια ώστε(i) Κάθε στοιχείο του
 είναι θετικός ακέραιος που δεν ξεπερνά το 2016.
είναι θετικός ακέραιος που δεν ξεπερνά το 2016.(ii) Για οποιαδήποτε στοιχεία
 του
του  , όχι απαραίτητα διαφορετικά μεταξύ τους, το γινόμενό τους
, όχι απαραίτητα διαφορετικά μεταξύ τους, το γινόμενό τους  δεν ανήκει στο
δεν ανήκει στο 
**********************************************
Φιλικά,
Αχιλλέας

 εχουμε οτι
εχουμε οτι  .
.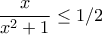 και το ζητούμενο γινεται προφανές.
και το ζητούμενο γινεται προφανές. Έστω ότι το ημικύκλιο διαμέτρου
Έστω ότι το ημικύκλιο διαμέτρου  Τότε
Τότε  (σχέση εγγεγραμμένης και γωνίας χορδής εφαπτομένης), οπότε το
(σχέση εγγεγραμμένης και γωνίας χορδής εφαπτομένης), οπότε το  είναι ορθογώνιο και ισοσκελές, άρα το
είναι ορθογώνιο και ισοσκελές, άρα το 
 τότε επειδή έχει ένα κοινό σημείο
τότε επειδή έχει ένα κοινό σημείο  (ως εγγεγραμμένες στο ίδιο τόξο). Άρα το
(ως εγγεγραμμένες στο ίδιο τόξο). Άρα το 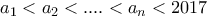 . Από την εκφώνηση προκύπτει ότι
. Από την εκφώνηση προκύπτει ότι 

 . Συνεπώς,
. Συνεπώς,  . Επομένως, αφού θέλουμε το μέγιστο ,
. Επομένως, αφού θέλουμε το μέγιστο , . (
. ( , δεν μπορεί ο
, δεν μπορεί ο  να περιέχεται στο
να περιέχεται στο 
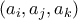 και για τις οποίες ισχύει
και για τις οποίες ισχύει  .
. στοιχεία.
στοιχεία. δεν είναι τέλειο τετράγωνο.
δεν είναι τέλειο τετράγωνο. με
με  , οι οποίες είναι
, οι οποίες είναι  το πλήθος. Τότε αφού
το πλήθος. Τότε αφού  από καθεμία από αυτές
από καθεμία από αυτές αριθμούς έχουμε πως είναι το πλήθος
αριθμούς έχουμε πως είναι το πλήθος 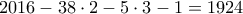
 .
. επιλέγουμε
επιλέγουμε  το οποίο ικανοποιεί τα ζητούμενα αφού το ελάχιστο δυνατό γινόμενο δύο στοιχείων είναι
το οποίο ικανοποιεί τα ζητούμενα αφού το ελάχιστο δυνατό γινόμενο δύο στοιχείων είναι  και άρα κανένα γινόμενο δύο στοιχείων του
και άρα κανένα γινόμενο δύο στοιχείων του 

 και προκύπτουν οι
και προκύπτουν οι 
 περιττός και
περιττός και  έχω
έχω  άρτιοι.
άρτιοι. .
. και παίρνω
και παίρνω 
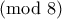 δίνει
δίνει  πράγμα άτοπο αφού
πράγμα άτοπο αφού 