Μαθηματική Ολυμπιάδα Α.Πετρούπολης 2015-16 (ΦΙ τάξη 11)

Al.Koutsouridis · #1

[b]Μαθηματική Ολυμπιάδα Αγίας Πετρούπολης 2015/16.

Θέματα της πρώτης φάσης για την 11η τάξη.[/b]

[b]1.[/b] Η εξίσωση $ax+\dfrac{c}{x}=b$ , στην οποία οι συντελεστές a,b

και

είναι μη μηδενικοί, έχει λύση. Αποδείξτε, ότι θα έχει λύση και μια εκ των εξισώσεων $ax+\dfrac{c}{x}=b+1$ και $ax+\dfrac{c}{x}=b-1$ .

[b]2.[/b] Σε κύκλο τοποθετήθηκαν οι αριθμοί από το

έως το

. Ο αριθμός ονομάζεται «καλός», αν διαιρείται με τον αριθμό, που βρίσκεται στα δεξιά του. Ποιο είναι το μέγιστο πλήθος καλών αριθμών που μπορεί να προκύψουν;

[b]3.[/b] Η διχοτόμος της γωνίας

ισοσκελούς τραπεζίου ABCD

τέμνει την βάση

στο σημείο

. Ο περιγεγραμμένος κύκλος του τριγώνου AKD

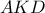τέμνει την πλευρά

στο σημείο

. Να αποδείξετε, ότι BL=KC

.

[b]4.[/b] Η συνάρτηση

για όλα τα $x,y \in \mathbb{R}$ ικανοποιεί την ανισότητα

$f(x^2+2y) \geq f(x^2+3y)$ .

Είναι γνωστό, ότι f(100)=100

. Να βρείτε το f(200)

.

[b]5.[/b] Στον πίνακα είναι γραμμένοι δυο αριθμοί: 10^6

και

. Επιτρέπετε να γράψουμε στον πίνακα τον αριθμητικό μέσο δυο ήδη γραμμένων αριθμών, αν αυτός ο αριθμός είναι ακέραιος και δεν έχει γραφεί νωρίτερα. Πόσους αριθμούς μπορούμε να γράψουμε με αυτόν τον τρόπο;

Ορέστης Λιγνός · #2

Al.Koutsouridis έγραψε: ↑
Κυρ Ιαν 07, 2018 1:26 pm

3. Η διχοτόμος της γωνίας ισοσκελούς τραπεζίου τέμνει την βάση στο σημείο . Ο περιγεγραμμένος κύκλος του τριγώνου τέμνει την πλευρά στο σημείο . Να αποδείξετε, ότι .

: ag.petroupoli-olympiad.png (25.57 KiB) Προβλήθηκε 992 φορές

Έστω ότι ο κύκλος τέμνει την

στο

.

Είναι $\widehat{LEC}=\widehat{LAD}$ , από το εγγεγραμμένο LEDA

και $\widehat{LAD}=\widehat{EDA}$ , άρα $\widehat{LEC}=\widehat{ADE} \Rightarrow LE \parallel AD \parallel BC$ (1).

Επίσης, από το ισοσκελές τραπέζιο ABCD

$\widehat{LBC}=\widehat{BCE}$ (2).

Από (1), (2), το BLEC

είναι ισοσκελές τραπέζιο.

Έτσι, BL=EC

(3).

Αν τώρα $\widehat{BAK}=\widehat{KAD}=\phi$ , είναι και $\widehat{KEC}=\phi$ (από το εγγεγραμένο KEDA

).

Ακόμη, $180^\circ-\widehat{KEC}-\widehat{CKE}=\widehat{KCE}=\widehat{BCD}=180^\circ-\widehat{BAD}=180^\circ-2\phi \Rightarrow$

$\widehat{KEC}+\widehat{CKE}=2\phi \Rightarrow \phi+\widehat{CKE}=2\phi \Rightarrow \widehat{CKE}=\phi=\widehat{KEC}$ , επομένως CK=CE

(4).

Από (3), (4), BL=CE=CK

ό.έ.δ.

Ορέστης Λιγνός · #3

Al.Koutsouridis έγραψε: ↑
Κυρ Ιαν 07, 2018 1:26 pm

4. Η συνάρτηση για όλα τα $x,y \in \mathbb{R}$ ικανοποιεί την ανισότητα

$f(x^2+2y) \geq f(x^2+3y)$ .

Είναι γνωστό, ότι . Να βρείτε το .

Έστω

η σχέση $f(x^2+2y) \geqslant f(x^2+3y)$ .

Τότε:

$N(20,-100) \,\, : f(200) \geqslant f(100)$ (1).

$N(0,50) \,\, : f(100) \geqslant f(150)$ (2).

$\displaystyle N(\sqrt{50},50) \,\, : f(150) \geqslant f(200)$ (3).

Από (2), (3) $f(100) \geqslant f(200)$ , και από (1), $f(200) \geqslant f(100)$ , άρα $f(200)=f(100)=100 \Rightarrow \,\boxed{f(200)=100}$ .

Ορέστης Λιγνός · #4

Al.Koutsouridis έγραψε: ↑
Κυρ Ιαν 07, 2018 1:26 pm

1. Η εξίσωση $ax+\dfrac{c}{x}=b$ , στην οποία οι συντελεστές και είναι μη μηδενικοί, έχει λύση. Αποδείξτε, ότι θα έχει λύση και μια εκ των εξισώσεων $ax+\dfrac{c}{x}=b+1$ και $ax+\dfrac{c}{x}=b-1$ .

Η $ax+\dfrac{c}{x}=b$ γράφεται ax^2-bx+c=0

, και αφού έχει λύση, είναι $\Delta_1=b^2-4ac \geqslant 0 \Rightarrow b^2 \geqslant 4ac$ (1).

Έστω ότι καμία εκ των εξισώσεων $ax+\dfrac{c}{x}=b+1$ και $ax+\dfrac{c}{x}=b-1$ δεν έχει λύση.

Τότε, $\Delta_2=(b -1)^2-4ac<0$ και $\Delta_3=(b+1)^2-4ac<0$ , επομένως (b-1)^2<4ac

(2) και

(3).

Από $(2)+(3) \Rightarrow (b+1)^2+(b-1)^2<8ac \Rightarrow 2b^2+2<8ac \Rightarrow b^2<4ac-1$ και από (1), $4ac \leqslant b^2<4ac-1$ , άτοπο.

Άρα, κάποια εκ των $ax+\dfrac{c}{x}=b+1$ και $ax+\dfrac{c}{x}=b-1$ έχει λύση.

Μαθηματική Ολυμπιάδα Α.Πετρούπολης 2015-16 (ΦΙ τάξη 11)

Μαθηματική Ολυμπιάδα Α.Πετρούπολης 2015-16 (ΦΙ τάξη 11)

Re: Μαθηματική Ολυμπιάδα Α.Πετρούπολης 2015-16 (ΦΙ τάξη 11)

Re: Μαθηματική Ολυμπιάδα Α.Πετρούπολης 2015-16 (ΦΙ τάξη 11)

Re: Μαθηματική Ολυμπιάδα Α.Πετρούπολης 2015-16 (ΦΙ τάξη 11)

Μέλη σε σύνδεση