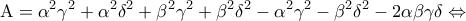Νίκο, δεν λέει πουθενά "διαδοχικοί όροι αριθμητικής προόδου".
ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Σιλουανός Μπραζιτίκος
Λέξεις Κλειδιά:
- DimitraAng1
- Δημοσιεύσεις: 3
- Εγγραφή: Κυρ Ιαν 29, 2017 2:29 pm
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Ααα τέλειαgeorge visvikis έγραψε: ↑Σάβ Ιαν 20, 2018 4:24 pmΠολύ σωστά!DimitraAng1 έγραψε: ↑Σάβ Ιαν 20, 2018 2:55 pmΔε θα μπορούσε να γίνει και με άλλο τρόπο; Επεκτείνοντας την ΕΓ μέχρι το Ζ (σημείο του κύκλου) και τραβώντας την ΑΖ; Τότε βρίσκουμε την ΖÂΒ επειδή βαίνει στο ίδιο τόξο με την ΖΓΒ και αποδεικνύουμε ότι Α = 90° Επειδή είναι ορθή βαίνει σε ημικύκλιο. Σωστά;george visvikis έγραψε: ↑Σάβ Ιαν 20, 2018 2:17 pmΘέμα 4 Γ Γυμνασίου Ευκλείδης 2018 Γ Γυμν .4.png
Έστωτο σημείο τομής της
με τη διχοτόμο της γωνίας
Επειδή το
είναι ισοσκελές θα είναι
Άρα τοβρίσκεται στη μεσοκάθετο του
αλλά και του
οπότε είναι το κέντρο του περιγεγραμμένου κύκλου.

 Ευχαριστώ! Έτσι έχω τρία θέματα σωστά
Ευχαριστώ! Έτσι έχω τρία θέματα σωστά  Καλή επιτυχία σε όλους!!!
Καλή επιτυχία σε όλους!!!-
kaliop1234
- Δημοσιεύσεις: 1
- Εγγραφή: Πέμ Νοέμ 16, 2017 9:09 pm
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13273
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13273
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Πρόβλημα 3 Γ Γυμνασίου
α)![\displaystyle \frac{{P(x) - P(y)}}{{x - y}} = \frac{{a[{{(x + 2)}^2} - {{(y + 2)}^2}] + b[(x + 3) - (y + 3)]}}{{x - y}} = \frac{{a(x + y + 4)(x - y) + b(x - y)}}{{x - y}} \displaystyle \frac{{P(x) - P(y)}}{{x - y}} = \frac{{a[{{(x + 2)}^2} - {{(y + 2)}^2}] + b[(x + 3) - (y + 3)]}}{{x - y}} = \frac{{a(x + y + 4)(x - y) + b(x - y)}}{{x - y}}](/forum/ext/geomar/texintegr/latexrender/pictures/dc504c3766f87e8f0d5368a1e1bcec49.png)
![\displaystyle \frac{{P(x) - P(y)}}{{x - y}} = \frac{{(x - y)[a(x + y + 4) + b]}}{{x - y}} = a(x + y + 4) + b \displaystyle \frac{{P(x) - P(y)}}{{x - y}} = \frac{{(x - y)[a(x + y + 4) + b]}}{{x - y}} = a(x + y + 4) + b](/forum/ext/geomar/texintegr/latexrender/pictures/82ac503195715ef21bfeeffbc1bbcec7.png) που είναι θετικός ακέραιος.
που είναι θετικός ακέραιος.
β) έστω όπου
όπου  θετικός ακέραιος. Από το προηγούμενο ερώτημα, υπάρχει θετικός ακέραιος
θετικός ακέραιος. Από το προηγούμενο ερώτημα, υπάρχει θετικός ακέραιος  ώστε:
ώστε:

που είναι πολλαπλάσιο του
α)
![\displaystyle \frac{{P(x) - P(y)}}{{x - y}} = \frac{{a[{{(x + 2)}^2} - {{(y + 2)}^2}] + b[(x + 3) - (y + 3)]}}{{x - y}} = \frac{{a(x + y + 4)(x - y) + b(x - y)}}{{x - y}} \displaystyle \frac{{P(x) - P(y)}}{{x - y}} = \frac{{a[{{(x + 2)}^2} - {{(y + 2)}^2}] + b[(x + 3) - (y + 3)]}}{{x - y}} = \frac{{a(x + y + 4)(x - y) + b(x - y)}}{{x - y}}](/forum/ext/geomar/texintegr/latexrender/pictures/dc504c3766f87e8f0d5368a1e1bcec49.png)
![\displaystyle \frac{{P(x) - P(y)}}{{x - y}} = \frac{{(x - y)[a(x + y + 4) + b]}}{{x - y}} = a(x + y + 4) + b \displaystyle \frac{{P(x) - P(y)}}{{x - y}} = \frac{{(x - y)[a(x + y + 4) + b]}}{{x - y}} = a(x + y + 4) + b](/forum/ext/geomar/texintegr/latexrender/pictures/82ac503195715ef21bfeeffbc1bbcec7.png) που είναι θετικός ακέραιος.
που είναι θετικός ακέραιος.β) έστω
 όπου
όπου  θετικός ακέραιος. Από το προηγούμενο ερώτημα, υπάρχει θετικός ακέραιος
θετικός ακέραιος. Από το προηγούμενο ερώτημα, υπάρχει θετικός ακέραιος  ώστε:
ώστε:
που είναι πολλαπλάσιο του

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Ωχ πράγματι. Θα επανέλθω πιο μετά.
Edit: Επανέρχομαι: Είναι
 με
με  φυσικούς, οπότε για
φυσικούς, οπότε για  έχουμε
έχουμε  . Όμως από Euler
. Όμως από Euler ![(a(w - z))^3 + (-wb)^3 + (cz)^3 = 3(z - w)wz\sqrt[3]{2018^2p^2q^2r^2} (a(w - z))^3 + (-wb)^3 + (cz)^3 = 3(z - w)wz\sqrt[3]{2018^2p^2q^2r^2}](/forum/ext/geomar/texintegr/latexrender/pictures/f68efdec885a30bb9257ffd54e73e272.png) όπου εύκολα το αριστερό μέλος είναι ακέραιος, άρα για να είναι και το δεξί πρέπει το
όπου εύκολα το αριστερό μέλος είναι ακέραιος, άρα για να είναι και το δεξί πρέπει το  κάτω από τη ρίζα να εμφανίζεται σε δύναμη που είναι πολλαπλάσιο του
κάτω από τη ρίζα να εμφανίζεται σε δύναμη που είναι πολλαπλάσιο του  , το οποίο εύκολα δεν γίνεται καθώς η δύναμη αυτή είναι είτε
, το οποίο εύκολα δεν γίνεται καθώς η δύναμη αυτή είναι είτε  είτε
είτε  .
.Edit 2: Πρέπει παραπάνω να εξετάσουμε και την περίπτωση
 που ισοδυναμεί με το να έχουμε 2 ίδιους όρους. Αυτό είναι απλό καθώς εξισώνοντας 2 από τους αριθμούς που δίνονται βρίσκουμε είτε
που ισοδυναμεί με το να έχουμε 2 ίδιους όρους. Αυτό είναι απλό καθώς εξισώνοντας 2 από τους αριθμούς που δίνονται βρίσκουμε είτε  είτε ότι κάποιος από τους
είτε ότι κάποιος από τους  είναι πολλαπλάσιο του 2018 (άρα όχι πρώτος).
είναι πολλαπλάσιο του 2018 (άρα όχι πρώτος).
τελευταία επεξεργασία από Nick1990 σε Σάβ Ιαν 20, 2018 9:28 pm, έχει επεξεργασθεί 4 φορές συνολικά.
Κολλιοπουλος Νικος.
Μεταδιδακτορικός ερευνητής.
Ερευνητικά ενδιαφέροντα: Στοχαστικές ΜΔΕ, ασυμπτωτική ανάλυση στοχαστικών συστημάτων, εφαρμογές αυτών στα χρηματοοικονομικά και στη διαχείριση ρίσκων.
Μεταδιδακτορικός ερευνητής.
Ερευνητικά ενδιαφέροντα: Στοχαστικές ΜΔΕ, ασυμπτωτική ανάλυση στοχαστικών συστημάτων, εφαρμογές αυτών στα χρηματοοικονομικά και στη διαχείριση ρίσκων.
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Μικρό το κακό νομίζω.Θα ισχύει κάτι του τύπου 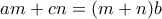 .Από ταυτότητα
.Από ταυτότητα  κλπ. βγαίνει το ζητούμενο.Τα υπόλοιπα ο Νίκος...
κλπ. βγαίνει το ζητούμενο.Τα υπόλοιπα ο Νίκος...
Edit:Ουσιαστικά το ίδιο: Αντί για την ειδική περίπτωση για διαδοχικούς όρους αριθμητικής προόδου, χρησιμοποιούμε
για διαδοχικούς όρους αριθμητικής προόδου, χρησιμοποιούμε  (βάζουμε ''βάρη'').Το τελείωμα ίδιο...
(βάζουμε ''βάρη'').Το τελείωμα ίδιο...
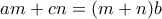 .Από ταυτότητα
.Από ταυτότητα  κλπ. βγαίνει το ζητούμενο.Τα υπόλοιπα ο Νίκος...
κλπ. βγαίνει το ζητούμενο.Τα υπόλοιπα ο Νίκος...Edit:Ουσιαστικά το ίδιο: Αντί για την ειδική περίπτωση
 για διαδοχικούς όρους αριθμητικής προόδου, χρησιμοποιούμε
για διαδοχικούς όρους αριθμητικής προόδου, χρησιμοποιούμε  (βάζουμε ''βάρη'').Το τελείωμα ίδιο...
(βάζουμε ''βάρη'').Το τελείωμα ίδιο...
τελευταία επεξεργασία από min## σε Σάβ Ιαν 20, 2018 8:45 pm, έχει επεξεργασθεί 2 φορές συνολικά.
-
kimjonarfib
- Δημοσιεύσεις: 34
- Εγγραφή: Σάβ Ιαν 07, 2017 8:17 pm
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
2 Γυμνασίου
Περιγραφικά:
Η μία ομάδα τελειώνει τ 1/4 του έργου σε 1/3 της ημέρας .Σε 1/3 της μέρας τελειώνουν τα 15 έργα οι 15/(1/4)=60 ομάδες.Για 5 μέρες χρειάζονται
60/(5/(1/3))=4 ομάδες.Για την λύση χρησιμοποιήσαμε ότι το εκάστοτε έργο που παράγεται είναι ανάλογο του πλήθους των ομάδων και ότι ο χρόνος που απαιτείται είναι αντιστρόφως ανάλογος του πλήθους των ομάδων.
Περιγραφικά:
Η μία ομάδα τελειώνει τ 1/4 του έργου σε 1/3 της ημέρας .Σε 1/3 της μέρας τελειώνουν τα 15 έργα οι 15/(1/4)=60 ομάδες.Για 5 μέρες χρειάζονται
60/(5/(1/3))=4 ομάδες.Για την λύση χρησιμοποιήσαμε ότι το εκάστοτε έργο που παράγεται είναι ανάλογο του πλήθους των ομάδων και ότι ο χρόνος που απαιτείται είναι αντιστρόφως ανάλογος του πλήθους των ομάδων.
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Μια λύση του ΘΕΜΑΤΟΣ 4/Α ΛΥΚΕΙΟΥ δημοσιεύθηκε εδώ.
Ακολουθεί μια άλλη ιδέα βασισμένη στη "γνωστή" σχέση
Παρατηρούμε ότι

κι άρα

ο οποίος λήγει σε 1 όταν διαιρεθεί με το
Έτσι, σκεφτόμαστε να βρούμε τα γινόμενα

και
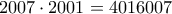
Προσθέτοντας κατά μέλη βρίσκουμε
(το και ο
και ο 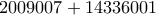 δεν λήγει σε
δεν λήγει σε  . Γι' αυτό υπολογίζουμε το επόμενο
. Γι' αυτό υπολογίζουμε το επόμενο  )
)
και τα υπόλοιπα συνεχίζονται όπως στην παραπάνω πρώτη λύση.
Φιλικά,
Αχιλλέας
Ακολουθεί μια άλλη ιδέα βασισμένη στη "γνωστή" σχέση

Παρατηρούμε ότι

κι άρα

ο οποίος λήγει σε 1 όταν διαιρεθεί με το

Έτσι, σκεφτόμαστε να βρούμε τα γινόμενα

και
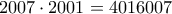
Προσθέτοντας κατά μέλη βρίσκουμε

(το
 και ο
και ο 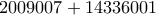 δεν λήγει σε
δεν λήγει σε  . Γι' αυτό υπολογίζουμε το επόμενο
. Γι' αυτό υπολογίζουμε το επόμενο  )
)και τα υπόλοιπα συνεχίζονται όπως στην παραπάνω πρώτη λύση.
Φιλικά,
Αχιλλέας
-
Παύλος Μαραγκουδάκης
- Επιμελητής
- Δημοσιεύσεις: 1513
- Εγγραφή: Παρ Ιαν 30, 2009 1:45 pm
- Τοποθεσία: Πειραιάς
- Επικοινωνία:
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Διαβάζοντας τη λύση τoυ Αχιλλέα για το 4o θέμα της Α Λυκείου έκανα την εξής σκέψη: Μπορεί να λυθεί χωρίς να βρεθούν οι ακέραιες λύσεις της εξίσωσης  αλλά παρατηρώντας την μορφή των λύσεων. Εφόσον οι
αλλά παρατηρώντας την μορφή των λύσεων. Εφόσον οι 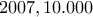 είναι πρώτοι μεταξύ τους η εξίσωση έχει σίγουρα ακέραια λύση
είναι πρώτοι μεταξύ τους η εξίσωση έχει σίγουρα ακέραια λύση  οπότε
οπότε  και
και  με
με  . Τα διαδοχικά
. Τα διαδοχικά  που είναι λύσεις απέχουν ακριβώς
που είναι λύσεις απέχουν ακριβώς  με άλλα λόγια σε κάθε
με άλλα λόγια σε κάθε  διαδοχικούς ακεραίους υπάρχει ακριβώς μία λύση. Οι εξαψήφιοι χωρίζονται ακριβώς σε
διαδοχικούς ακεραίους υπάρχει ακριβώς μία λύση. Οι εξαψήφιοι χωρίζονται ακριβώς σε  ομάδες των
ομάδες των  άρα έχουμε ακριβώς
άρα έχουμε ακριβώς  λύσεις.
λύσεις.
 αλλά παρατηρώντας την μορφή των λύσεων. Εφόσον οι
αλλά παρατηρώντας την μορφή των λύσεων. Εφόσον οι 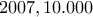 είναι πρώτοι μεταξύ τους η εξίσωση έχει σίγουρα ακέραια λύση
είναι πρώτοι μεταξύ τους η εξίσωση έχει σίγουρα ακέραια λύση  οπότε
οπότε  και
και  με
με  . Τα διαδοχικά
. Τα διαδοχικά  που είναι λύσεις απέχουν ακριβώς
που είναι λύσεις απέχουν ακριβώς  με άλλα λόγια σε κάθε
με άλλα λόγια σε κάθε  διαδοχικούς ακεραίους υπάρχει ακριβώς μία λύση. Οι εξαψήφιοι χωρίζονται ακριβώς σε
διαδοχικούς ακεραίους υπάρχει ακριβώς μία λύση. Οι εξαψήφιοι χωρίζονται ακριβώς σε  ομάδες των
ομάδες των  άρα έχουμε ακριβώς
άρα έχουμε ακριβώς  λύσεις.
λύσεις.Στάλα τη στάλα το νερό το μάρμαρο τρυπά το,
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Δεν ξέρω γιατί δεν επέλεξαν για τη γωνία Α το μέτρο
 και άφησαν ένα τέτοιο απογοητευτικό αριθμό ως απάντηση !!!
και άφησαν ένα τέτοιο απογοητευτικό αριθμό ως απάντηση !!!Και του χρόνου-Καλά αποτελέσματα σε όλα τα παιδιά !!!
-
Athena apo
- Δημοσιεύσεις: 23
- Εγγραφή: Κυρ Δεκ 04, 2016 7:41 pm
-
Eleftheria
- Δημοσιεύσεις: 28
- Εγγραφή: Τρί Οκτ 04, 2016 3:07 pm
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5284
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Μια ακόμα λύση για το 4ο θέμα της Β΄ Γυμνασίου
Έστω ο αριθμός των κερμάτων δύο ευρώ. Ο
ο αριθμός των κερμάτων δύο ευρώ. Ο  πρέπει να είναι φυσικός μικρότερος του
πρέπει να είναι φυσικός μικρότερος του  . Τότε είναι
. Τότε είναι  ο αριθμός των κερμάτων του ενός ευρώ.
ο αριθμός των κερμάτων του ενός ευρώ.
Ο Γιάννης ξόδεψε ευρώ την πρώτη μέρα.
ευρώ την πρώτη μέρα.
Τού έμειναν ευρώ, οπότε ξόδεψε
ευρώ, οπότε ξόδεψε  ευρώ τη δεύτερη μέρα.
ευρώ τη δεύτερη μέρα.
Η εξίσωση έχει ρίζα
έχει ρίζα  .
.
Έστω
 ο αριθμός των κερμάτων δύο ευρώ. Ο
ο αριθμός των κερμάτων δύο ευρώ. Ο  πρέπει να είναι φυσικός μικρότερος του
πρέπει να είναι φυσικός μικρότερος του  . Τότε είναι
. Τότε είναι  ο αριθμός των κερμάτων του ενός ευρώ.
ο αριθμός των κερμάτων του ενός ευρώ.Ο Γιάννης ξόδεψε
 ευρώ την πρώτη μέρα.
ευρώ την πρώτη μέρα.Τού έμειναν
 ευρώ, οπότε ξόδεψε
ευρώ, οπότε ξόδεψε  ευρώ τη δεύτερη μέρα.
ευρώ τη δεύτερη μέρα.Η εξίσωση
 έχει ρίζα
έχει ρίζα  .
.- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5284
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Μια λύση για το θέμα 2 της Γ΄ Γυμνασίου:
Θεωρούμε σταθερή την απόδοση της ομάδας.
Η εκφώνηση είναι ισοδύναμη με την εξής διατύπωση:
Πόσες τέτοιες ομάδες εργατών της ιδίας απόδοσης χρειάζονται για να τελειώσουν ίδια έργα σε μία ημέρα;
ίδια έργα σε μία ημέρα;
Η ομάδα τελειώνει τα ενός έργου σε μία μέρα, άρα
ενός έργου σε μία μέρα, άρα  ίδιες ομάδες θα τελειώσουν
ίδιες ομάδες θα τελειώσουν  ίδια έργα σε μία ημέρα, δηλαδή
ίδια έργα σε μία ημέρα, δηλαδή  ίδια έργα σε
ίδια έργα σε  ημέρες.
ημέρες.
Αναρωτιέμαι αν αυτό το (όμορφο για άλλες περιπτώσεις) θέμα είναι επιπέδου Γ΄ Γυμνασίου σε διαγωνισμό ΕΥΚΛΕΙΔΗ;
Θεωρούμε σταθερή την απόδοση της ομάδας.
Η εκφώνηση είναι ισοδύναμη με την εξής διατύπωση:
Πόσες τέτοιες ομάδες εργατών της ιδίας απόδοσης χρειάζονται για να τελειώσουν
 ίδια έργα σε μία ημέρα;
ίδια έργα σε μία ημέρα; Η ομάδα τελειώνει τα
 ενός έργου σε μία μέρα, άρα
ενός έργου σε μία μέρα, άρα  ίδιες ομάδες θα τελειώσουν
ίδιες ομάδες θα τελειώσουν  ίδια έργα σε μία ημέρα, δηλαδή
ίδια έργα σε μία ημέρα, δηλαδή  ίδια έργα σε
ίδια έργα σε  ημέρες.
ημέρες.Αναρωτιέμαι αν αυτό το (όμορφο για άλλες περιπτώσεις) θέμα είναι επιπέδου Γ΄ Γυμνασίου σε διαγωνισμό ΕΥΚΛΕΙΔΗ;
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Ωραία ιδέα, Παύλο, και πιο κοντά στο διαγωνιστικό πνεύμα!Παύλος Μαραγκουδάκης έγραψε: ↑Σάβ Ιαν 20, 2018 9:09 pmΔιαβάζοντας τη λύση τoυ Αχιλλέα για το 4o θέμα της Α Λυκείου έκανα την εξής σκέψη: Μπορεί να λυθεί χωρίς να βρεθούν οι ακέραιες λύσεις της εξίσωσηςαλλά παρατηρώντας την μορφή των λύσεων. Εφόσον οι
είναι πρώτοι μεταξύ τους η εξίσωση έχει σίγουρα ακέραια λύση
οπότε
και
με
. Τα διαδοχικά
που είναι λύσεις απέχουν ακριβώς
με άλλα λόγια σε κάθε
διαδοχικούς ακεραίους υπάρχει ακριβώς μία λύση. Οι εξαψήφιοι χωρίζονται ακριβώς σε
ομάδες των
άρα έχουμε ακριβώς
λύσεις.
Εμμέσως απάντησες και σε μια απορία-σκέψη που είχα εάν έπρεπε οι μαθητές να βρουν οπωσδήποτε τους αριθμούς αυτούς.
Ισως δεν είναι τυχαίο ότι το θέμα ζητούσε απλώς να βρουν το πλήθος τους.
Φιλικά,
Αχιλλέας
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Παύλο πολύ ωραία ιδέα!!Παύλος Μαραγκουδάκης έγραψε: ↑Σάβ Ιαν 20, 2018 9:09 pmΔιαβάζοντας τη λύση τoυ Αχιλλέα για το 4o θέμα της Α Λυκείου έκανα την εξής σκέψη: Μπορεί να λυθεί χωρίς να βρεθούν οι ακέραιες λύσεις της εξίσωσηςαλλά παρατηρώντας την μορφή των λύσεων. Εφόσον οι
είναι πρώτοι μεταξύ τους η εξίσωση έχει σίγουρα ακέραια λύση
οπότε
και
με
. Τα διαδοχικά
που είναι λύσεις απέχουν ακριβώς
με άλλα λόγια σε κάθε
διαδοχικούς ακεραίους υπάρχει ακριβώς μία λύση. Οι εξαψήφιοι χωρίζονται ακριβώς σε
ομάδες των
άρα έχουμε ακριβώς
λύσεις.
Αλέξανδρος Συγκελάκης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 2 επισκέπτες

 τους 3 αριθμούς, ώστε
τους 3 αριθμούς, ώστε  , τότε
, τότε 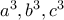 είναι ακέραιοι και
είναι ακέραιοι και