Θέματα της δεύτερης φάσης (τελικής) για την 8η τάξη.[/i][/b]
[b]1.[/b] Σε κύκλο κάθονται
 άτομα μερικοί από τους οποίους είναι ντόμπροι και οι υπόλοιποι ψεύτες. Ο Αντώνης ρώτησε τον καθένα τους: «Από τα γειτονικά σου άτομα πόσοι είναι ψεύτες;» και άθροισε τους αριθμούς που προέκυψαν. Ύστερα η Άννα έκανε το ίδιο. Απαντώντας στην ερώτηση, οι ντόμπροι λένε πάντα την αλήθεια και οι ψεύτες πάντα ψέματα, αλλά μόνο τους αριθμούς
άτομα μερικοί από τους οποίους είναι ντόμπροι και οι υπόλοιποι ψεύτες. Ο Αντώνης ρώτησε τον καθένα τους: «Από τα γειτονικά σου άτομα πόσοι είναι ψεύτες;» και άθροισε τους αριθμούς που προέκυψαν. Ύστερα η Άννα έκανε το ίδιο. Απαντώντας στην ερώτηση, οι ντόμπροι λένε πάντα την αλήθεια και οι ψεύτες πάντα ψέματα, αλλά μόνο τους αριθμούς  ,
,  ή
ή  . Θα μπορούσε άραγε το άθροισμα των αριθμών του Αντώνη να είναι κατά
. Θα μπορούσε άραγε το άθροισμα των αριθμών του Αντώνη να είναι κατά  μεγαλύτερο, αυτού της Άννας;
μεγαλύτερο, αυτού της Άννας;[b]2.[/b] Στο εσωτερικό της γωνίας
 , ίσης με
, ίσης με  , δίνεται σημείο
, δίνεται σημείο  , τέτοιο ώστε
, τέτοιο ώστε  και
και  . Στο τμήμα
. Στο τμήμα  διαλέγεται σημείο
διαλέγεται σημείο  έτσι, ώστε
έτσι, ώστε  . Να αποδείξετε, ότι
. Να αποδείξετε, ότι 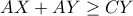 .
.[b]3.[/b] Ο Βασίλης τοποθέτησε σε όλα τα κελιά ενός πίνακα
 τους αριθμούς από το
τους αριθμούς από το  έως το
έως το  από μία φορά. Ο Πέτρος διαλέγει ένα κελί του πίνακα, τοποθετεί σε αυτό ένα πιόνι και θέλει να κάνει όσο το δυνατόν περισσότερες κινήσεις έτσι, ώστε ο αριθμός υπό το πιόνι συνεχώς να αυξάνεται. Με μια κίνηση ο Πέτρος μπορεί να μετακινήσει το πιόνι σε οποιοδήποτε κελί ενός τετραγώνου
από μία φορά. Ο Πέτρος διαλέγει ένα κελί του πίνακα, τοποθετεί σε αυτό ένα πιόνι και θέλει να κάνει όσο το δυνατόν περισσότερες κινήσεις έτσι, ώστε ο αριθμός υπό το πιόνι συνεχώς να αυξάνεται. Με μια κίνηση ο Πέτρος μπορεί να μετακινήσει το πιόνι σε οποιοδήποτε κελί ενός τετραγώνου  με κέντρο το κελί της τρέχουσας θέσης του πιονιού (το πιόνι θα πρέπει να παραμένει στα όρια του πίνακα με αυτές τις κινήσεις). Ποιος είναι ο μεγαλύτερος αριθμός κινήσεων που εγγυημένα μπορεί να κάνει ο Πέτρος, ανεξάρτητα από το πως θα τοποθετήσει τους αριθμούς ο Βασίλης.
με κέντρο το κελί της τρέχουσας θέσης του πιονιού (το πιόνι θα πρέπει να παραμένει στα όρια του πίνακα με αυτές τις κινήσεις). Ποιος είναι ο μεγαλύτερος αριθμός κινήσεων που εγγυημένα μπορεί να κάνει ο Πέτρος, ανεξάρτητα από το πως θα τοποθετήσει τους αριθμούς ο Βασίλης.[b]4.[/b] Στον πίνακα είναι γραμμένος θετικός ακέραιος αριθμός. Κάθε λεπτό στον αριθμό του πίνακα προστίθεται το άθροισμα των
 πρώτων ψηφίων του. Να αποδείξετε, ότι μετά από κάποιο χρονικό διάστημα τρεις συνεχόμενες φορές θα εμφανιστεί αριθμός που δεν διαιρείτε με το
πρώτων ψηφίων του. Να αποδείξετε, ότι μετά από κάποιο χρονικό διάστημα τρεις συνεχόμενες φορές θα εμφανιστεί αριθμός που δεν διαιρείτε με το  .
.[b]Καταληκτική αίθουσα[/b]
[b]5.[/b] Στο κυρτό τετράπλευρο
 το σημείο
το σημείο  είναι το μέσο της πλευράς
είναι το μέσο της πλευράς  ,
,  ,
,  και
και  . Να βρείτε την γωνία
. Να βρείτε την γωνία  .
.[b]6.[/b] Το άθροισμα των θετικών αριθμών
 και
και  είναι ίσο με
είναι ίσο με  . Να δείξετε, ότι
. Να δείξετε, ότι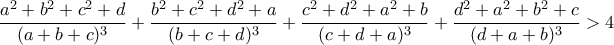
[b]7.[/b] Μια χώρα έχει
 πόλεις, μερικά ζεύγη πόλεων είναι συνδεδεμένα με δρόμο, εξάλλου από κάθε πόλη μπορούμε να μεταβούμε μέσο δρόμων σε οποιαδήποτε άλλη. Για οποιεσδήποτε δυο πόλεις
πόλεις, μερικά ζεύγη πόλεων είναι συνδεδεμένα με δρόμο, εξάλλου από κάθε πόλη μπορούμε να μεταβούμε μέσο δρόμων σε οποιαδήποτε άλλη. Για οποιεσδήποτε δυο πόλεις  και
και  που συνδέονται με δρόμο θα βρεθούν άλλες δυο
που συνδέονται με δρόμο θα βρεθούν άλλες δυο  και
και  τέτοιες, ώστε οποιεσδήποτε δυο εκ των τεσσάρων αυτών πόλεων να συνδέονται με δρόμο. Να αποδείξετε, ότι μπορούμε να κλείσουμε για έργα μερικούς δρόμους έτσι, ώστε το πλήθος των πόλεων από τις οποίες εξέρχονται ακριβώς δυο δρόμοι, να γίνει μικρότερο του
τέτοιες, ώστε οποιεσδήποτε δυο εκ των τεσσάρων αυτών πόλεων να συνδέονται με δρόμο. Να αποδείξετε, ότι μπορούμε να κλείσουμε για έργα μερικούς δρόμους έτσι, ώστε το πλήθος των πόλεων από τις οποίες εξέρχονται ακριβώς δυο δρόμοι, να γίνει μικρότερο του  , και σε αυτήν την περίπτωση μεταξύ δυο οποιονδήποτε πόλεων να μείνει μοναδική διαδρομή, που δεν διέρχεται δυο φορές από τον ίδιο δρόμο.
, και σε αυτήν την περίπτωση μεταξύ δυο οποιονδήποτε πόλεων να μείνει μοναδική διαδρομή, που δεν διέρχεται δυο φορές από τον ίδιο δρόμο.
 , για να ασχοληθούν οι νεώτεροι και αργότερα αν χρειαστεί " ανοίγουμε " πλήρως τη λύση :
, για να ασχοληθούν οι νεώτεροι και αργότερα αν χρειαστεί " ανοίγουμε " πλήρως τη λύση : .
. . Επίσης,
. Επίσης,  .
. από
από  .
. , και αρκεί
, και αρκεί 
 ώστε
ώστε 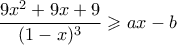
 .
. , άρα και στην (1), η ισότητα θέλουμε να ισχύει για
, άρα και στην (1), η ισότητα θέλουμε να ισχύει για 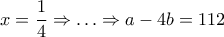 .
.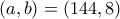 η (1) γράφεται
η (1) γράφεται  , που ισχύει.
, που ισχύει. για
για  διαδοχικά και προσθέτοντας κατά μέλη,
διαδοχικά και προσθέτοντας κατά μέλη,  .
. .
.

 ,
,

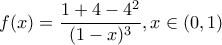 :
:
 ,
, 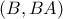 που τέμνονται στο
που τέμνονται στο  .
. .
. είναι ίσα (
είναι ίσα ( ), άρα
), άρα  .
. , όπου στο τέλος χρησιμοποιήθηκε η τριγωνική ανισότητα στο
, όπου στο τέλος χρησιμοποιήθηκε η τριγωνική ανισότητα στο  .
. .
.


 . Είναι
. Είναι  θετικοί με
θετικοί με  .
. τότε:
τότε: και άρα
και άρα  και
και  και άρα
και άρα  .
.
 οπότε
οπότε 


 , παίρνουμε ότι
, παίρνουμε ότι  και
και 

 . Οπότε
. Οπότε  ,
,