Βρείτε όλες τις πραγματικές τιμές των
 , έτσι ώστε:
, έτσι ώστε:
Πρόβλημα 2
Κάποιος έγραψε σε
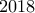 χαρτάκια από έναν διαφορετικό ακέραιο αριθμό από το
χαρτάκια από έναν διαφορετικό ακέραιο αριθμό από το  μέχρι και το
μέχρι και το 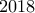 . Στη συνέχεια, ανακάτεψε τα χαρτάκια και τα έβαλε σε φακέλους, έτσι ώστε ο κάθε φάκελος να περιέχει
. Στη συνέχεια, ανακάτεψε τα χαρτάκια και τα έβαλε σε φακέλους, έτσι ώστε ο κάθε φάκελος να περιέχει  χαρτάκια. Τέλος, έγραψε σε κάθε φάκελο την απόλυτη τιμή της διαφοράς των δύο αριθμών που περιέχει. Αν το τελευταίο ψηφίο των αριθμών που αναγράφονται στους φακέλους είναι μόνο
χαρτάκια. Τέλος, έγραψε σε κάθε φάκελο την απόλυτη τιμή της διαφοράς των δύο αριθμών που περιέχει. Αν το τελευταίο ψηφίο των αριθμών που αναγράφονται στους φακέλους είναι μόνο  και
και  , να υπολογίσετε το τελευταίο ψηφίο του αθροίσματος των αριθμών που είναι αναγραμμένοι στους φακέλους.
, να υπολογίσετε το τελευταίο ψηφίο του αθροίσματος των αριθμών που είναι αναγραμμένοι στους φακέλους. Πρόβλημα 3
Δίνεται ένα παραλληλόγραμμο
 . Φέρουμε από το σημείο
. Φέρουμε από το σημείο  ευθεία
ευθεία  κάθετη προς την ευθεία
κάθετη προς την ευθεία  και από το σημείο
και από το σημείο  ευθεία
ευθεία  κάθετη προς την ευθεία
κάθετη προς την ευθεία  . Έστω
. Έστω  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών  . Αν ο κύκλος με κέντρο το σημείο
. Αν ο κύκλος με κέντρο το σημείο  και ακτίνα
και ακτίνα  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  και την ευθεία
και την ευθεία  στο σημείο
στο σημείο  , αποδείξτε ότι η ευθεία
, αποδείξτε ότι η ευθεία  διέρχεται από το σημείο
διέρχεται από το σημείο  .
. Πρόβλημα 4
Δίνονται δύο σημεία στο επίπεδο και ένας πραγματικός αριθμός
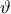 , όπου
, όπου  . Παίζουμε το εξής παιγνίδι:
. Παίζουμε το εξής παιγνίδι: Σε κάθε βήμα επιλέγουμε ένα από τα δύο σημεία, και το περιστρέφουμε αριστερόστροφα κατά γωνία
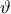 γύρω από το άλλο σημείο.
γύρω από το άλλο σημείο.Για να κερδίσουμε το παιχνίδι, θα πρέπει να καταφέρουμε να ανταλλάξουμε τις αρχικές θέσεις των δύο σημείων.
(α) Αν
 , να αποδείξετε ότι δεν μπορούμε να κερδίσουμε το παιχνίδι.
, να αποδείξετε ότι δεν μπορούμε να κερδίσουμε το παιχνίδι.(β) Να εξετάσετε αν υπάρχει
![\displaystyle{\vartheta\in\left(0, \frac{\pi}{2}\right]} \displaystyle{\vartheta\in\left(0, \frac{\pi}{2}\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/8f2946d55d586dbdcf5286edd56aca0d.png) , για το οποίο μπορούμε να κερδίσουμε το παιχνίδι, περιγράφοντας με σαφήνεια την σκέψη σας.
, για το οποίο μπορούμε να κερδίσουμε το παιχνίδι, περιγράφοντας με σαφήνεια την σκέψη σας.
 κι επειδή
κι επειδή  θα είναι
θα είναι 
 η εξίσωση και είναι:
η εξίσωση και είναι: 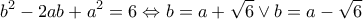





 κατασκευάστηκε παραλληλόγραμμο, 2ο) Τα τρίγωνα
κατασκευάστηκε παραλληλόγραμμο, 2ο) Τα τρίγωνα  είναι όμοια.
είναι όμοια.
 δεσπόζει η αντικατάσταση
δεσπόζει η αντικατάσταση  με αρχικό στόχο τον προσδιορισμό του
με αρχικό στόχο τον προσδιορισμό του  Έτσι για αυτόν που γνωρίζει την κλασική αυτή μέθοδο το πρώτο θέμα θα μπορούσε, εκτός της άριστης πράγματι επίλυσης από τον Γιώργο Βισβίκη, να λυθεί και ως εξής:
Έτσι για αυτόν που γνωρίζει την κλασική αυτή μέθοδο το πρώτο θέμα θα μπορούσε, εκτός της άριστης πράγματι επίλυσης από τον Γιώργο Βισβίκη, να λυθεί και ως εξής:  Έτσι παίρνουμε
Έτσι παίρνουμε  ή με απαλοιφή του
ή με απαλοιφή του  , παίρνουμε
, παίρνουμε  από όπου έχουμε
από όπου έχουμε 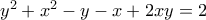 ή
ή  (συμπλήρωση για «παραγωγή» ταυτότητας) ή
(συμπλήρωση για «παραγωγή» ταυτότητας) ή 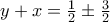 , με χρήση πλέον της οποίας προσδιορίζονται εύκολα οι
, με χρήση πλέον της οποίας προσδιορίζονται εύκολα οι  άρα και οι
άρα και οι 
 και τους μικρούς σε ένα σύνολο
και τους μικρούς σε ένα σύνολο  . Επομένως αν
. Επομένως αν  είναι το άθροισμα όλων των αριθμών που είναι αναγραμμένοι στους φακέλους, τότε
είναι το άθροισμα όλων των αριθμών που είναι αναγραμμένοι στους φακέλους, τότε 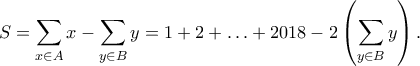
 από τους αναγραφόμενους τελειώνουν σε
από τους αναγραφόμενους τελειώνουν σε  , τότε
, τότε  τελειώνουν σε
τελειώνουν σε  .
. στην παραπάνω παίρνουμε:
στην παραπάνω παίρνουμε: 
 . Τότε
. Τότε 
 .
.