Ας συμβολίσουμε τις εννιάδες ως

. Τα

καθορίζονται πλήρως από τα

. Ουσιαστικά λοιπόν θέλουμε τα

να είναι όλα διαφορετικά μεταξύ τους.
Αυτό αντιστοιχεί σε κάτι που ονομάζεται Latin transversal. Πιο συγκεκριμένα φτιάχνουμε ένα πίνακα με σειρές και στήλες αριθμημένες από το

ως το

. Στο κελί

τοποθετούμε το άθροισμα

modulo

. Κάθε αριθμός εμφανίζεται ακριβώς μία φορά σε κάθε σειρά και κάθε στήλη. Κάθε πίνακας με αυτήν την ιδιότητα ονομάζεται Latin square. Αυτό που ψάχνουμε είναι να επιλέξουμε ένα ακριβώς 9 κελιά, ένα από κάθε σειρά και κάθε στήλη ώστε οι τιμές τους να είναι διαφορετικές. Αυτό ονομάζεται Latin transversal.
Η ύπαρξη/απαρίθμηση των Latin transversals είναι εν γένει δύσκολο πρόβλημα. Η απάντηση στο ερώτημα που έθεσες βρίσκεται στην σελίδα
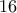 εδώ
εδώ και είναι

.
Μπορούμε να δούμε ότι η απάντηση είναι πολλαπλάσιο του

αφού για κάθε παράδειγμα, αν προσθέσουμε (modulo 9)

σε κάθε ψηφίο των δεκάδων και αφαιρέσουμε

από κάθε ψηφίο των μονάδων θα πάρουμε ένα καινούργιο παράδειγμα. Έτσι τα παραδείγματα έρχονται σε εννιάδες (εννιάδων).
 .
. .
. }. Πιθανώς να υπάρχουν πολύ περισσότερες, ίσως όμως και όχι...
}. Πιθανώς να υπάρχουν πολύ περισσότερες, ίσως όμως και όχι...
 . Τα
. Τα  καθορίζονται πλήρως από τα
καθορίζονται πλήρως από τα  . Ουσιαστικά λοιπόν θέλουμε τα
. Ουσιαστικά λοιπόν θέλουμε τα  ως το
ως το  τοποθετούμε το άθροισμα
τοποθετούμε το άθροισμα  modulo
modulo 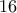
 .
. σε κάθε ψηφίο των δεκάδων και αφαιρέσουμε
σε κάθε ψηφίο των δεκάδων και αφαιρέσουμε