Το στυλ του διαγωνισμού ξεφεύγει από το σύνηθες μοτίβο που επιτάσσει ο κάθε διαγωνιζόμενος να γράφει μόνος του. Η κάθε χώρα διαγωνίζεται ομαδικά. Αυτή είναι μία βασική διαφορά, αλλά όχι η μόνη. Περισσότερες πληροφορίες αντλεί κανείς από εδώ.
Οι διαγωνιζόμενες χώρες είναι (όπως προδίδει και το όνομα του διαγωνισμού) σχεδόν όλες οι χώρες της λεκάνης της Μεσογείου.
Φέτος, πρώτοι ήρθαν οι Ιταλοί και δεύτεροι οι Γάλλοι.
Η δυσκολία των προβλημάτων ποικίλει. Άλλα είναι πολύ απλά, αλλά μερικά είναι πιο απαιτητικά. Εδώ θα αναρτήσω μερικά από αυτά.

Πρόβλημα GE1B, Early afternoon round-First Stage.
 Θεωρούμε όλες τις συναρτήσεις
Θεωρούμε όλες τις συναρτήσεις  . Πόσες από αυτές ικανοποιούν ταυτόχρονα τις συνθήκες:
. Πόσες από αυτές ικανοποιούν ταυτόχρονα τις συνθήκες: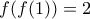 και
και  ;
;
 .
. τότε
τότε  , άτοπο.
, άτοπο. πρέπει
πρέπει  . Πρέπει επίσης
. Πρέπει επίσης 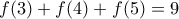 . Μπορούμε να γράψουμε το
. Μπορούμε να γράψουμε το  ως
ως  με
με 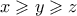 και
και 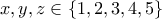 με τους πιο κάτω τρόπους:
με τους πιο κάτω τρόπους:  . (Κατά αντίστροφη λεξικογραφική σειρά.) Τα
. (Κατά αντίστροφη λεξικογραφική σειρά.) Τα  και
και 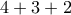 δίνουν από
δίνουν από  διαφορετικές συναρτήσεις. Τα
διαφορετικές συναρτήσεις. Τα  και
και  από
από  και το
και το  μία. Άρα σε αυτήν την περίπτωση έχουμε
μία. Άρα σε αυτήν την περίπτωση έχουμε  διαφορετικές συναρτήσεις.
διαφορετικές συναρτήσεις. πρέπει
πρέπει  . Πρέπει επίσης
. Πρέπει επίσης  . Μπορούμε να γράψουμε το
. Μπορούμε να γράψουμε το  ως:
ως:  που δίνουν
που δίνουν  διαφορετικές συναρτήσεις.
διαφορετικές συναρτήσεις.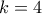 πρέπει
πρέπει  . Πρέπει επίσης
. Πρέπει επίσης 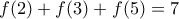 . Μπορούμε να γράψουμε το
. Μπορούμε να γράψουμε το  ως:
ως:  που δίνουν
που δίνουν  διαφορετικές συναρτήσεις.
διαφορετικές συναρτήσεις. πρέπει
πρέπει  . Πρέπει επίσης
. Πρέπει επίσης  . Μπορούμε να γράψουμε το
. Μπορούμε να γράψουμε το  που δίνουν
που δίνουν  διαφορετικές συναρτήσεις.
διαφορετικές συναρτήσεις.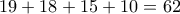 διαφορετικές συναρτήσεις.
διαφορετικές συναρτήσεις.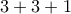 στην περίπτωση
στην περίπτωση  , ο οποίος είναι πολλαπλάσιο του
, ο οποίος είναι πολλαπλάσιο του  και κάθε ψηφίο του είναι
και κάθε ψηφίο του είναι  ή
ή  .
. οπότε το
οπότε το  διαιρεί το τελευταίο ψηφίο του
διαιρεί το τελευταίο ψηφίο του  οπότε είναι το
οπότε είναι το 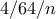 οπότε ο
οπότε ο  θα διαιρεί τα δύο τελευταία ψηφία του αριθμού (
θα διαιρεί τα δύο τελευταία ψηφία του αριθμού ( ή
ή  ) οπότε το προτελευταίο ψηφίο του
) οπότε το προτελευταίο ψηφίο του 
 οπότε ο
οπότε ο  ή
ή  ) οπότε το
) οπότε το  ψηφίο του
ψηφίο του 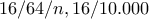 οπότε όπως και πριν
οπότε όπως και πριν 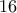 θα διαιρεί τα
θα διαιρεί τα  ή
ή  ) οπότε το
) οπότε το 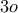 του ψηφίο είναι το
του ψηφίο είναι το  πότε ο
πότε ο  διαιρεί τα τελευταία
διαιρεί τα τελευταία  ψηφία του αριθμού... οπότε βρίσκουμε πως το
ψηφία του αριθμού... οπότε βρίσκουμε πως το  ψηφίο είναι το
ψηφίο είναι το  διαιρεί τον
διαιρεί τον  αλλά όχι τον
αλλά όχι τον 

 ψηφία ο
ψηφία ο 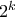
 για την οποία ισχύει
για την οποία ισχύει και
και  για κάθε θετικό ακέραιο
για κάθε θετικό ακέραιο  για κάθε περιττό
για κάθε περιττό  , ο οποίος δεν είναι της μορφής
, ο οποίος δεν είναι της μορφής 
 υπάρχουν, ώστε
υπάρχουν, ώστε 
 οπότε θα βρούμε όλους τους αριθμούς
οπότε θα βρούμε όλους τους αριθμούς  για τους οποίους με τις δοσμένες ισότητες καταλήγουν στο
για τους οποίους με τις δοσμένες ισότητες καταλήγουν στο 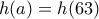
 δηλαδή τους αριθμούς
δηλαδή τους αριθμούς  και οι αριθμοί που είναι κατά ένα μεγαλύτεροι από τους προαναφερθέντες εκτός του
και οι αριθμοί που είναι κατά ένα μεγαλύτεροι από τους προαναφερθέντες εκτός του  δηλαδή οι
δηλαδή οι  . (o
. (o  απορρίπτεται)
απορρίπτεται)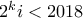 δηλαδή οι αριθμοί
δηλαδή οι αριθμοί  και αυτοί που είανι κατά ένα μεγαλύτεροι από αυτούς δηλαδή οι
και αυτοί που είανι κατά ένα μεγαλύτεροι από αυτούς δηλαδή οι 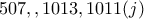
 δηλαδή ο αριθμός
δηλαδή ο αριθμός  και αυτός που είναι κατά ένα μεγαλύτερος δηλαδή ο
και αυτός που είναι κατά ένα μεγαλύτερος δηλαδή ο 