Demetres έγραψε: ↑Πέμ Μάιος 02, 2019 6:20 pm
A5. Έστω κοίλη συνάρτηση

και συνεχής συνάρτηση

. Αν

για κάθε

, να αποδειχθεί ότι η

είναι πολυώνυμο δευτέρου βαθμού.
Δεν είναι σαφές τουλάχιστον σε μένα ποιος είναι ο ορισμός της κοίλης.
Αν πάρουμε τον κανονικό ορισμό τότε αποδεικνύεται ότι μια κοίλη συνάρτηση
έχει πλευρικές παραγώγους .Το ίδιο ισχύει και για τις κυρτές.
Θα δείξω κάτι γενικότερο από αυτό που ζητάει.
Έστω συναρτήσεις

και

. Αν η

έχει πλευρικές
παραγώγους και

(*)
για κάθε

, να αποδειχθεί ότι η

είναι πολυώνυμο το πολύ δευτέρου βαθμού.
Λύση.
Η (*) γράφεται
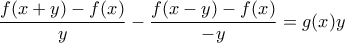
παίρνοντας

βλέπουμε ότι οι πλευρικές παράγωγοι είναι ίσες.
Αρα η

είναι παραγωγίσημη οπότε λόγω της (*) και η

είναι παραγωγίσημη .
Παραγωγίζουμε την (*) ως προς

Παίρνουμε

Για

γίνεται

Από την τελευταία συμπεραίνουμε ότι υπάρχει η

.
Παραγωγίζοντας την (1) ως προς

παίρνουμε

Ενώ παραγωγίζοντας την (1) ως προς

παίρνουμε
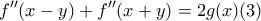
Προσθέτοντας της (2)(3) έχουμε

Η τελευταία για

δίνει
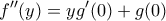
Από αυτήν εύκολα παίρνουμε ότι η

είναι πολυώνυμο το πολύ

βαθμού.
Αν λοιπόν είναι

τότε αντικαθιστώντας στην (*) εχουμε
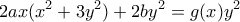
Αλλά για
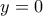
από την τελευταία συμπεραίνουμε ότι

Τελικά αποδείξαμε ότι η

είναι πολυώνυμο το πολύ δευτέρου βαθμού.
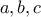 ώστε
ώστε  . Να αποδειχθεί ότι:
. Να αποδειχθεί ότι:
 . Να αποδειχθεί ότι:
. Να αποδειχθεί ότι:
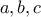 ώστε
ώστε  . Να αποδειχθεί ότι:
. Να αποδειχθεί ότι:
 και συνεχής συνάρτηση
και συνεχής συνάρτηση  . Αν
. Αν
 , να αποδειχθεί ότι η
, να αποδειχθεί ότι η  είναι πολυώνυμο δευτέρου βαθμού.
είναι πολυώνυμο δευτέρου βαθμού. και πραγματικοί αριθμοί
και πραγματικοί αριθμοί  . Να αποδειχθεί ότι:
. Να αποδειχθεί ότι:


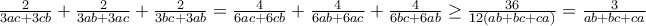 από
από 
 όπου κάνοντας τις πράξεις καταλήγουμε στο
όπου κάνοντας τις πράξεις καταλήγουμε στο 
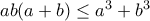 όμοια και στις άλλες περιπτώσεις.
όμοια και στις άλλες περιπτώσεις. που αποδυκνύεται εύκολα από
που αποδυκνύεται εύκολα από 
 , διότι ισοδυναμεί με την προφανή
, διότι ισοδυναμεί με την προφανή 
![a+b+c\geq 3\sqrt[3]{abc}=3 a+b+c\geq 3\sqrt[3]{abc}=3](/forum/ext/geomar/texintegr/latexrender/pictures/4f73cf7860dc28acf692bdd22c860524.png) από την ανισότητα αριθμητικού- γεωμετρικού μέσου.
από την ανισότητα αριθμητικού- γεωμετρικού μέσου.

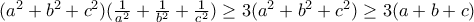
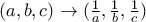 παίρνουμε την ανισότητα
παίρνουμε την ανισότητα 
 η ανίσωση γίνεται
η ανίσωση γίνεται 







![\displaystyle \frac{a}{b} + \frac{a}{b} + \frac{b}{c} \geqslant 3 \sqrt[3]{\frac{a^2}{bc}} = a. \displaystyle \frac{a}{b} + \frac{a}{b} + \frac{b}{c} \geqslant 3 \sqrt[3]{\frac{a^2}{bc}} = a.](/forum/ext/geomar/texintegr/latexrender/pictures/db761179884c8174a14330d1309d0b29.png)

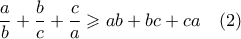



 . Αναπτύσσοντας η ζητούμενη ανισότητα γίνεται:
. Αναπτύσσοντας η ζητούμενη ανισότητα γίνεται:![\displaystyle 4[12,6,0] + 2[6,6,6] \geqslant 3[8,5,5] + 3[7,7,4] \displaystyle 4[12,6,0] + 2[6,6,6] \geqslant 3[8,5,5] + 3[7,7,4]](/forum/ext/geomar/texintegr/latexrender/pictures/92d2feee4cec8a808db79e4c18f8c8f0.png)
![[p,q,r] = \sum_{sym} x^py^qz^r [p,q,r] = \sum_{sym} x^py^qz^r](/forum/ext/geomar/texintegr/latexrender/pictures/99f7f66d68ca34b3b94d4ac6582c083d.png) .
.![[12,6,0] \geqslant [6,6,6] [12,6,0] \geqslant [6,6,6]](/forum/ext/geomar/texintegr/latexrender/pictures/31afb44fe720e7360ea8a37c2057e31f.png) αρκεί να δείξουμε ότι
αρκεί να δείξουμε ότι ![[12,6,0] + [6,6,6] \geqslant [8,5,5] + [7,7,4] [12,6,0] + [6,6,6] \geqslant [8,5,5] + [7,7,4]](/forum/ext/geomar/texintegr/latexrender/pictures/a2c6774d3281df22c3bdaf01464e8e70.png) .
. και
και  παίρνουμε
παίρνουμε![\displaystyle [12,6,0] + [6,6,6] \geqslant [10,4,4] + [8,8,2] \geqslant [8,5,5] + [7,7,4] \displaystyle [12,6,0] + [6,6,6] \geqslant [10,4,4] + [8,8,2] \geqslant [8,5,5] + [7,7,4]](/forum/ext/geomar/texintegr/latexrender/pictures/292d585a654e4f4cc86c0033638186e6.png)
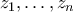 . Να αποδειχθεί ότι:
. Να αποδειχθεί ότι:
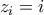 για κάθε
για κάθε  .
. .
. .
. .
.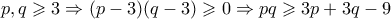 , επομένως αρκεί να δείξω ότι
, επομένως αρκεί να δείξω ότι  , που είναι προφανές, αφού
, που είναι προφανές, αφού  .
. .
. , οπότε αρκεί
, οπότε αρκεί  (1).
(1). , οπότε αρκεί
, οπότε αρκεί  (2).
(2).
 , που ισχύει από τον Ισχυρισμό.
, που ισχύει από τον Ισχυρισμό. .
. , με
, με  ισχύει ότι
ισχύει ότι  .
. .
. .
.![\displaystyle (1+\dfrac{n-k}{1})(1+\dfrac{n-k}{2}) \cdots (1+\dfrac{n-k}{k}) \geqslant (1+\dfrac{n-k}{\sqrt[k]{k!}})^k \displaystyle (1+\dfrac{n-k}{1})(1+\dfrac{n-k}{2}) \cdots (1+\dfrac{n-k}{k}) \geqslant (1+\dfrac{n-k}{\sqrt[k]{k!}})^k](/forum/ext/geomar/texintegr/latexrender/pictures/ca41feb71d0b722d57dcc0c13c571123.png) , οπότε μετά από πράξεις αρκεί να δείξω ότι (ο θετικός παράγοντας
, οπότε μετά από πράξεις αρκεί να δείξω ότι (ο θετικός παράγοντας  ''φεύγει'')
''φεύγει'')  .
.![\sqrt[k]{k!} \leqslant \dfrac{k+1}{2} \sqrt[k]{k!} \leqslant \dfrac{k+1}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/d1fb46cb85d7a24ed4e6bb7d2cdae664.png) .
.![\sqrt[k]{k!} =\sqrt[k]{1 \cdot 2 \cdots k} \leqslant \dfrac{1+2+ \cdots+k}{k}=\dfrac{k+1}{2} \sqrt[k]{k!} =\sqrt[k]{1 \cdot 2 \cdots k} \leqslant \dfrac{1+2+ \cdots+k}{k}=\dfrac{k+1}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/d16fd3ae1d7ae9e936207c5a928acf7d.png) .
. .
. .
. , από την ΑΜ-ΓΜ. Από την Chebychev, παίρνω ότι
, από την ΑΜ-ΓΜ. Από την Chebychev, παίρνω ότι  , και
, και  .
.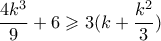 , ή ισοδύναμα,
, ή ισοδύναμα, 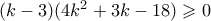 , που είναι προφανές, αφού
, που είναι προφανές, αφού  .
.

 (ακροβατικό)
(ακροβατικό)
 (0)
(0) (1)
(1)
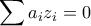




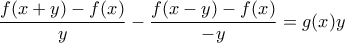

 είναι παραγωγίσημη .
είναι παραγωγίσημη . Παίρνουμε
Παίρνουμε 
 γίνεται
γίνεται 
 .
. παίρνουμε
παίρνουμε 
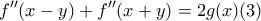

 δίνει
δίνει 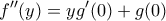
 βαθμού.
βαθμού.
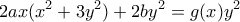
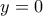 από την τελευταία συμπεραίνουμε ότι
από την τελευταία συμπεραίνουμε ότι 
 .
.
 όπου
όπου 
 για κάθε
για κάθε  .
.
 όπου
όπου  , θέλουμε να δείξουμε ότι:
, θέλουμε να δείξουμε ότι:
 με τον ίδιο σταθερό συντελεστή. Οπότε αν αφαιρέσουμε το δεξί από το αριστερό μέλος, μένει να δείξουμε ότι:
με τον ίδιο σταθερό συντελεστή. Οπότε αν αφαιρέσουμε το δεξί από το αριστερό μέλος, μένει να δείξουμε ότι:![\displaystyle [(k+1)^2 - 4i(k+1-i)]m^2 + [(k+1)^3 - 4(k+1)i(k+1-i)]m \geqslant 0 \displaystyle [(k+1)^2 - 4i(k+1-i)]m^2 + [(k+1)^3 - 4(k+1)i(k+1-i)]m \geqslant 0](/forum/ext/geomar/texintegr/latexrender/pictures/d2ddf7cd22825504fbff037c09518583.png)
 το οποίο είναι άμεσο από Cauchy-Schwarz.
το οποίο είναι άμεσο από Cauchy-Schwarz. ήταν με πολυώνυμο στο
ήταν με πολυώνυμο στο  του οποίου πάλι ο σταθερός συντελεστής ήταν
του οποίου πάλι ο σταθερός συντελεστής ήταν 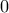 .)
.) για κάθε
για κάθε  .
. , μετά από πράξεις καταλήγουμε στο:
, μετά από πράξεις καταλήγουμε στο: 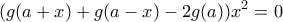
 και αφού η
και αφού η  από όπου καταλήγουμε ότι η
από όπου καταλήγουμε ότι η  είναι δευτεροβάθμια και επειδή είναι κοίλη, τότε και ως συνάρτηση στο
είναι δευτεροβάθμια και επειδή είναι κοίλη, τότε και ως συνάρτηση στο  είναι δευτεροβάθμια.
είναι δευτεροβάθμια.