ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Κυρ Απρ 09, 2023 12:11 am
Al.Koutsouridis έγραψε: ↑Κυρ Απρ 09, 2023 12:03 am
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Σάβ Απρ 08, 2023 11:33 pm
Αν έχω καταλάβει σωστά το τι ζητάει η άσκηση, έτσι όπως έχει δοθεί στην μετάφραση (Η φράση: "σε αυτή την πρόταση", θεώρησα ότι έλεγε:
"σε αυτόν τον ακέραιο αριθμό"), τότε:
Ας θεωρήσω π.χ τον αριθμό
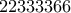
Τότε:

από τα

ψηφία του διαιρούνται με το


από τα

ψηφία του διαιρούνται με το


από τα

ψηφία του διαιρούνται με το

και το

Άρα μια απάντηση είναι: Το

των ψηφίων διαιρείται με το

, το
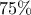
των ψηφίων διαιρείται με το

και το
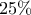
των ψηφίων διαιρείται με το

και με το

.
Φυσικά μπορούν να δοθούν πάρα πολλές απαντήσεις. Για παράδειγμα, αν θεωρήσουμε τον αριθμό
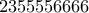
, τότε:
Το

των ψηφίων διαιρείται με το

, το

των ψηφίων διαιρείται με το

και το
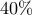
των ψηφίων,
διαιρείται με το

και το

.
(Μήπως κάτι άλλο εννοεί στην εκφώνηση;)
Την εκφώνηση την έχω μεταφέρει σωστά. Αυτό που εννοεί είναι, ας χρησιμοποιήσουμε το πρώτο παράδειγμα που δώσατε ως πρόταση:
"Σε αυτήν την πρόταση το

των ψηφίων διαιρείται με το

, το
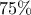
των ψηφίων διαιρείται με το

και το
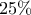
των ψηφίων διαιρείται με το

και με το

."
Στην πρόταση συμμετέχουν τα ψηφία
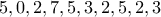
. Από αυτά διαιρούνται με το

τέσσερα ψηφία από σύνολο δέκα, δηλαδή το

των ψηφίων της πρότασης. Άρα, το παράδειγμα αυτό δεν μας δίνει αληθή πρόταση.
Ωραία. Θεώρησα ότι δεν είχε ίσως αποδοθεί σωστά η μετάφραση. Τώρα έγινε πλήρως κατανοητό για το τι ζητάει.
Οπότε θα το κοιτάξω αύριο ξανά.
Ας δούμε την λύση : (Την γράφω πολύ αναλυτικά, για να φανεί η μοναδικότητα της λύσης, αν και αυτό δεν το ζητάει η άσκηση, οπότε
θα μπορούσε κάποιος πολύ πιο σύντομα να βρει την απάντηση)
Αρχικά είναι φανερό, ότι οι ακέραιοι που ζητάμε, πρέπει να είναι οπωσδήποτε διψήφιοι.
Πράγματι, αν ήταν όλοι μονοψήφιοι, έστω
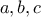
, τότε η δοσμένη πρόταση θα περιλάμβανε τα ψηφία:
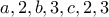
.
Το πλήθος αυτών είναι
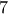
, οπότε αποκλείεται οι αριθμοί

να είναι ακέραιοι (πράγματι, για παράδειγμα τα ψηφία που διαιρούνται
με το

θα ήταν τουλάχιστον

και το πολύ

, οπότε κανένα από τα ποσοστά:
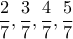
δεν είναι ακέραιο επί τοις %.)
Αν πάλι, ο πρώτος εκ των ακεραίων που ζητάμε ήταν διψήφιος , έστω

και οι άλλοι δύο μονοψήφιοι, έστω
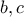
, τότε η δοσμένη
πρόταση θα περιλάμβανε τα ψηφία
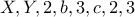
, που είναι

στο πλήθος. Αν τώρα για παράδειγμα με το

διαιρούνταν
μόνο τα δύο δυάρια, τότε το αντίστοιχο ποσοστό θα ήταν

, δηλαδή
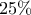
, που είναι άτοπο, αφού τότε θα είναι
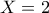
και τα δυάρια θα ήταν

και όχι

. Αν πάλι με το

διαιρούνται

από τους παραπάνω αριθμούς, τότε το ποσοστό
των ψηφίων που διαιρούνται με το

θα είναι

που είναι μη ακέραιο ποσοστό επί τοις % και απορρίπτεται.
Αν με το

διαιρούνται

αριθμοί, τότε το αντίστοιχο ποσοστό θα είναι
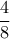
, δηλαδή

, άρα
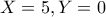
Τότε η πρόταση θα περιλάμβανε τα ψηφία
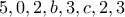
. Τώρα βλέπουμε ότι με το

διαιρούνται τουλάχιστον

και το
πολύ

αριθμοί οπότε το ποσοστό

θα είναι διψήφιος, άτοπο.
Αν τα δύο πρώτα ποσοστά ήταν διψήφιοι, έστω

και

, και το τρίτο μονοψήφιος, έστω

, τότε η δοσμένη πρόταση
θα περιλάμβανε τα ψηφία:
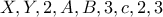
, που είναι

στο πλήθος και άρα δεν θα ήταν δυνατόν να είχαμε ακέραιο
ποσοστό επί τοις %.
Συμπεραίνουμε λοιπόν, ότι όλα τα ποσοστά που ζητάμε, είναι αριθμοί διψήφιοι, έστω
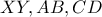
. Τότε η δοσμένη πρόταση
περιλαμβάνει τα ψηφία :
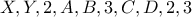
τα οποία είναι

στο πλήθος, οπότε τα ποσοστά που ζητάμε , αφού είναι
ακέραιοι αριθμοί, θα λήγουν σε μηδέν. Άρα

και άρα η πρότασή μας περιλαμβάνει τα ψηφία:
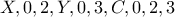
Διακρίνουμε τις περιπτώσεις:
(α)
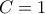
. Τότε το ποσοστό των ψηφίων που διαιρούνται με το

και το

, θα είναι

.
Άρα πρέπει να έχουμε μόνο ένα εξάρι. Αν

, τότε με το

πρέπει να διαιρούνται τα

ακριβώς από τα ψηφία.
(δηλαδή τα ψηφία:
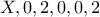
). Άρα το
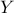
δεν πρέπει να διαιρείται με το

. Όμως, κοιτώντας το ποιοι αριθμοί
διαιρούνται με το

, βλέπουμε ότι είναι οι
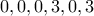
και το ποσοστό αυτό πρέπει να είναι
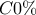
. Αφού όμως το

δεν πρέπει να διαιρείται με το

, ενώ πρέπει και να είναι μεγαλύτερο ή ίσο του

, άρα θα είναι ή

, ή

, πράγμα άτοπο,
αφού τότε τα ψηφία που διαιρούνται με το

θα ήταν σε ποσοστό ή
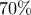
ή
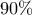
, που προφανώς δεν είναι
(β) Αν
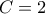
, ή
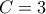
, ή
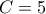
, τότε ομοίως καταλήγουμε σε άτοπο. (Το

, δεν είναι δυνατόν να είναι μεγαλύτερο
του

, γιατί δεν γίνεται οι αριθμοί που διαιρούνται με το

και το

έχουν ποσοστό πάνω από το

ενώ όσοι διαιρούνται
π.χ από το

να έχουν ποσοστό μικρότερο από το

)
(γ). Μας μένει μόνο η περίπτωση
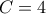
. Εύκολα τώρα βλέπουμε ότι η τελική πρόταση που ζητάμε να συμπληρώσουμε είναι η εξής:
" Το
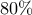
των ψηφίων αυτής της πρότασης διαιρούνται με το

, το

διαιρούνται με το

και το
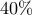
διαιρούνται με το

και με το

"
ΠΑΡΑΤΗΡΗΣΗ: Για την περίπτωση
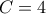
, υπάρχει και μια ακόμα αληθής πρόταση:
"Το
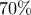
των ψηφίων αυτής της πρότασης διαιρούνται με το

, το

διαιρούνται με το

και το
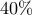
διαιρούνται με το

και με το

"
ΕΥΧΑΡΙΣΤΩ τον Αλέξανδρο Κουτσουρίδη, που το παρατήρησε και με ενημέρωσε.
Συνεπώς οι απαντήσεις στο πρόβλημα είναι δύο.
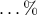 των ψηφίων διαιρείται με το
των ψηφίων διαιρείται με το  , το
, το 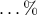 των ψηφίων διαιρείται με το
των ψηφίων διαιρείται με το  και το
και το 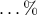 των ψηφίων διαιρείται και με το
των ψηφίων διαιρείται και με το  και με το
και με το  .
. ορθογώνιου τριγώνου
ορθογώνιου τριγώνου  διαλέγουμε σημείο
διαλέγουμε σημείο  , για το οποίο
, για το οποίο 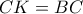 . Το τμήμα
. Το τμήμα 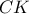 τέμνει την διχοτόμο
τέμνει την διχοτόμο  στο μέσο της. Να βρείτε τις γωνίες του τριγώνου
στο μέσο της. Να βρείτε τις γωνίες του τριγώνου  .
. και
και  (
( ,
,  και
και  μη μηδενικοί αριθμοί) έχουν κοινή ρίζα. Βρείτε την.
μη μηδενικοί αριθμοί) έχουν κοινή ρίζα. Βρείτε την. , εκτός του κεντρικού, είναι τοποθετημένο ένα από δυο σήματα: «στροφή» ή «ευθεία». Αυτοκίνητο εισέρχεται από το εξωτερικό σε τυχαίο κελί του συνόρου του τετραγώνου, ύστερα από το οποίο κινείται παράλληλα προς τις πλευρές των κελιών, τηρώντας δυο κανόνες:
, εκτός του κεντρικού, είναι τοποθετημένο ένα από δυο σήματα: «στροφή» ή «ευθεία». Αυτοκίνητο εισέρχεται από το εξωτερικό σε τυχαίο κελί του συνόρου του τετραγώνου, ύστερα από το οποίο κινείται παράλληλα προς τις πλευρές των κελιών, τηρώντας δυο κανόνες: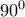 (σε οποιαδήποτε μεριά της δικιάς του επιλογής)
(σε οποιαδήποτε μεριά της δικιάς του επιλογής) 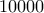 . Μετά από αυτό, καθώς το άθροισμα όλων των αριθμών γίνει ίσο με
. Μετά από αυτό, καθώς το άθροισμα όλων των αριθμών γίνει ίσο με 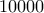 , το παιχνίδι τελειώνει υπολογίζοντας το άθροισμα των ψηφίων σε κάθε ήμισυ του πίνακα. Κερδίζει αυτός, στου οποίου το ήμισυ το άθροισμα των ψηφίων είναι μικρότερο (σε περίπτωση ίσων αθροισμάτων έχουμε ισοπαλία). Μπορεί κάποιος εκ των δυο παιχτών να κερδίσει, ανεξάρτητα του πως θα παίξει ο αντίπαλος;
, το παιχνίδι τελειώνει υπολογίζοντας το άθροισμα των ψηφίων σε κάθε ήμισυ του πίνακα. Κερδίζει αυτός, στου οποίου το ήμισυ το άθροισμα των ψηφίων είναι μικρότερο (σε περίπτωση ίσων αθροισμάτων έχουμε ισοπαλία). Μπορεί κάποιος εκ των δυο παιχτών να κερδίσει, ανεξάρτητα του πως θα παίξει ο αντίπαλος;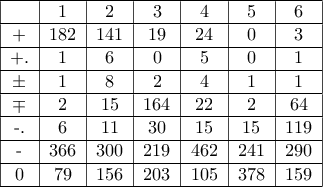

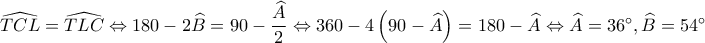
 η κοινή ρίζα.
η κοινή ρίζα.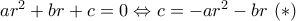
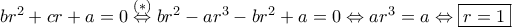
 και τα δυο κάτω είναι συμμετρικά ως προς το σημείο
και τα δυο κάτω είναι συμμετρικά ως προς το σημείο  .
.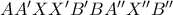 , ώστε
, ώστε 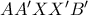 να μεταφέρεται με στροφή γύρω από το σημείο
να μεταφέρεται με στροφή γύρω από το σημείο 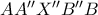 (Σχήμα 3)
(Σχήμα 3)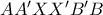 να είναι κεντρικά συμμετρική
να είναι κεντρικά συμμετρική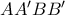 , η διαγώνιος του οποίου είναι ίση με την πλευρά του (σχήμα 4). Σε αυτό η κορυφή
, η διαγώνιος του οποίου είναι ίση με την πλευρά του (σχήμα 4). Σε αυτό η κορυφή 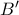 μεταφέρεται στην κορυφή
μεταφέρεται στην κορυφή  με περιστροφή γύρω από το σημείο
με περιστροφή γύρω από το σημείο 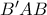 , άρα ικανοποιείται η συνθήκη (1). Τώρα δεν είναι δύσκολο να επιτύχουμε: μπορούμε να διαλέξουμε δυο σημεία
, άρα ικανοποιείται η συνθήκη (1). Τώρα δεν είναι δύσκολο να επιτύχουμε: μπορούμε να διαλέξουμε δυο σημεία  και
και  , ύστερα να διαλέξουμε ως
, ύστερα να διαλέξουμε ως 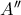 ,
, 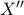 και
και 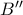 τις εικόνες των σημείων
τις εικόνες των σημείων  ,
, 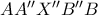 να μην τέμνονται και επίσης και οι δυο να μην τέμνονται με το τμήμα
να μην τέμνονται και επίσης και οι δυο να μην τέμνονται με το τμήμα  .
.  οι τεθλασμένες δεν τέμνονται, αν όλα τα σημεία τους κείτονται (προβάλλονται σε ευθεία, κάθετη προς την
οι τεθλασμένες δεν τέμνονται, αν όλα τα σημεία τους κείτονται (προβάλλονται σε ευθεία, κάθετη προς την 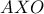 να είναι αμβλεία (για να βρεθεί τέτοιο σημείο, το αρχικό παραλληλόγραμμο
να είναι αμβλεία (για να βρεθεί τέτοιο σημείο, το αρχικό παραλληλόγραμμο 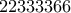
 από τα
από τα  ψηφία του διαιρούνται με το
ψηφία του διαιρούνται με το 
 από τα
από τα 
 των ψηφίων διαιρείται με το
των ψηφίων διαιρείται με το 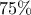 των ψηφίων διαιρείται με το
των ψηφίων διαιρείται με το 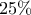 των ψηφίων διαιρείται με το
των ψηφίων διαιρείται με το 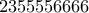 , τότε:
, τότε: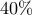 των ψηφίων,
των ψηφίων,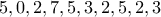 . Από αυτά διαιρούνται με το
. Από αυτά διαιρούνται με το  των ψηφίων της πρότασης. Άρα, το παράδειγμα αυτό δεν μας δίνει αληθή πρόταση.
των ψηφίων της πρότασης. Άρα, το παράδειγμα αυτό δεν μας δίνει αληθή πρόταση.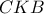 φέρνω τη διάμεσο
φέρνω τη διάμεσο  ( που είναι διχοτόμος και ύψος ).
( που είναι διχοτόμος και ύψος ). το συμμετρικό του
το συμμετρικό του  ως προς ο μέσο
ως προς ο μέσο  της
της 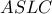 είναι ορθογώνιο κι έτσι κάθε κίτρινη γωνία είναι :
είναι ορθογώνιο κι έτσι κάθε κίτρινη γωνία είναι : 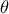
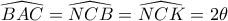 ( η πρώτη ισότητα γιατί είναι οξείες με πλευρές κάθετες)
( η πρώτη ισότητα γιατί είναι οξείες με πλευρές κάθετες)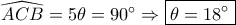 . Προφανές τώρα
. Προφανές τώρα 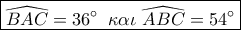
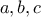 , τότε η δοσμένη πρόταση θα περιλάμβανε τα ψηφία:
, τότε η δοσμένη πρόταση θα περιλάμβανε τα ψηφία: 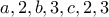 .
. 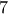 , οπότε αποκλείεται οι αριθμοί
, οπότε αποκλείεται οι αριθμοί  να είναι ακέραιοι (πράγματι, για παράδειγμα τα ψηφία που διαιρούνται
να είναι ακέραιοι (πράγματι, για παράδειγμα τα ψηφία που διαιρούνται , οπότε κανένα από τα ποσοστά:
, οπότε κανένα από τα ποσοστά: 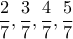
 και οι άλλοι δύο μονοψήφιοι, έστω
και οι άλλοι δύο μονοψήφιοι, έστω 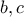 , τότε η δοσμένη
, τότε η δοσμένη 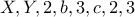 , που είναι
, που είναι  , δηλαδή
, δηλαδή 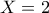 και τα δυάρια θα ήταν
και τα δυάρια θα ήταν  που είναι μη ακέραιο ποσοστό επί τοις % και απορρίπτεται.
που είναι μη ακέραιο ποσοστό επί τοις % και απορρίπτεται.  αριθμοί, τότε το αντίστοιχο ποσοστό θα είναι
αριθμοί, τότε το αντίστοιχο ποσοστό θα είναι 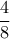 , δηλαδή
, δηλαδή 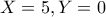
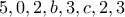 . Τώρα βλέπουμε ότι με το
. Τώρα βλέπουμε ότι με το  θα είναι διψήφιος, άτοπο.
θα είναι διψήφιος, άτοπο. , και το τρίτο μονοψήφιος, έστω
, και το τρίτο μονοψήφιος, έστω  , τότε η δοσμένη πρόταση
, τότε η δοσμένη πρόταση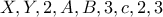 , που είναι
, που είναι  στο πλήθος και άρα δεν θα ήταν δυνατόν να είχαμε ακέραιο
στο πλήθος και άρα δεν θα ήταν δυνατόν να είχαμε ακέραιο 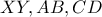 . Τότε η δοσμένη πρόταση
. Τότε η δοσμένη πρόταση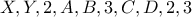 τα οποία είναι
τα οποία είναι  στο πλήθος, οπότε τα ποσοστά που ζητάμε , αφού είναι
στο πλήθος, οπότε τα ποσοστά που ζητάμε , αφού είναι  και άρα η πρότασή μας περιλαμβάνει τα ψηφία:
και άρα η πρότασή μας περιλαμβάνει τα ψηφία: 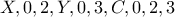
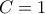 . Τότε το ποσοστό των ψηφίων που διαιρούνται με το
. Τότε το ποσοστό των ψηφίων που διαιρούνται με το  .
. , τότε με το
, τότε με το  ακριβώς από τα ψηφία.
ακριβώς από τα ψηφία. 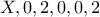 ). Άρα το
). Άρα το 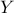 δεν πρέπει να διαιρείται με το
δεν πρέπει να διαιρείται με το 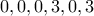 και το ποσοστό αυτό πρέπει να είναι
και το ποσοστό αυτό πρέπει να είναι 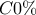 . Αφού όμως το
. Αφού όμως το 
 , ή
, ή 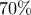 ή
ή 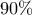 , που προφανώς δεν είναι
, που προφανώς δεν είναι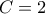 , ή
, ή 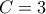 , ή
, ή 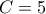 , τότε ομοίως καταλήγουμε σε άτοπο. (Το
, τότε ομοίως καταλήγουμε σε άτοπο. (Το 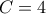 . Εύκολα τώρα βλέπουμε ότι η τελική πρόταση που ζητάμε να συμπληρώσουμε είναι η εξής:
. Εύκολα τώρα βλέπουμε ότι η τελική πρόταση που ζητάμε να συμπληρώσουμε είναι η εξής: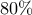 των ψηφίων αυτής της πρότασης διαιρούνται με το
των ψηφίων αυτής της πρότασης διαιρούνται με το  διαιρούνται με το
διαιρούνται με το