Πρόβλημα 1:
(α) Αν
 φυσικός αριθμός ο οποίος δεν είναι πολλαπλάσιο του
φυσικός αριθμός ο οποίος δεν είναι πολλαπλάσιο του  , να αποδείξετε ότι ο
, να αποδείξετε ότι ο  είναι πολλαπλάσιο του 3.
είναι πολλαπλάσιο του 3.(β) Να βρείτε όλους τους πρώτους αριθμούς
 έτσι ώστε ο
έτσι ώστε ο 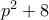 να είναι επίσης πρώτος αριθμός.
να είναι επίσης πρώτος αριθμός.Πρόβλημα 2: Δίνεται ισοσκελές τρίγωνο

 με τις γωνίες της βάσης του να είναι
με τις γωνίες της βάσης του να είναι  . Από το μέσον
. Από το μέσον  του
του  φέρουμε ευθεία κάθετη προς την
φέρουμε ευθεία κάθετη προς την  η οποία τέμνει την
η οποία τέμνει την  στο σημείο
στο σημείο  . Πάνω στην προέκταση της
. Πάνω στην προέκταση της  , προς το
, προς το  , παίρνουμε σημείο
, παίρνουμε σημείο  τέτοιο ώστε
τέτοιο ώστε  . Η παράλληλη από το σημείο
. Η παράλληλη από το σημείο  προς την
προς την  τέμνει την
τέμνει την  στο σημείο
στο σημείο  . Αν οι παράλληλες από τα σημεία
. Αν οι παράλληλες από τα σημεία  και
και  προς τις ευθείες
προς τις ευθείες  και
και  αντίστοιχα τέμνονται στο σημείο
αντίστοιχα τέμνονται στο σημείο  , να υπολογίσετε την γωνία
, να υπολογίσετε την γωνία  .
.Πρόβλημα 3: Ο Αντρέας και ο Βασίλης συμφωνούν να παίξουν ένα παιχνίδι με αριθμούς ως εξής:
«Γράφουν εναλλάξ στον πίνακα θετικά τέλεια τετράγωνα με τον όρο ότι ένα τέλειο τετράγωνο μπορεί να γραφεί αρκετές φορές.»
Αν το άθροισμα των αριθμών που είναι γραμμένοι στον πίνακα γίνει μεγαλύτερο του
 αυτός που έγραψε τον τελευταίο αριθμό χάνει το παιχνίδι.
αυτός που έγραψε τον τελευταίο αριθμό χάνει το παιχνίδι.Αν ο Αντρέας ξεκινά πρώτος το παιχνίδι να βρείτε ποιος από τους δύο παίκτες έχει στρατηγική νίκης και να εξηγήσετε την στρατηγική.
Πρόβλημα 4: Σε μια τάξη κάθε μαθητής παίζει τουλάχιστον ένα μουσικό όργανο από τα μουσικά όργανα κιθάρα, βιολί και πιάνο. Ξέρουμε ότι:
 Τουλάχιστον
Τουλάχιστον  των μαθητών παίζει κιθάρα ή βιολί ή και τα δύο.
των μαθητών παίζει κιθάρα ή βιολί ή και τα δύο. Τουλάχιστον
Τουλάχιστον  των μαθητών παίζει βιολί ή πιάνο ή και τα δύο.
των μαθητών παίζει βιολί ή πιάνο ή και τα δύο. Τουλάχιστον
Τουλάχιστον  των μαθητών παίζει πιάνο ή κιθάρα ή και τα δύο.
των μαθητών παίζει πιάνο ή κιθάρα ή και τα δύο.Υπάρχει επίσης αριθμός
 (όχι απαραίτητα ακέραιος αριθμός) ώστε
(όχι απαραίτητα ακέραιος αριθμός) ώστε Τουλάχιστον
Τουλάχιστον  των μαθητών που παίζουν κιθάρα, παίζουν μόνο κιθάρα.
των μαθητών που παίζουν κιθάρα, παίζουν μόνο κιθάρα. Τουλάχιστον
Τουλάχιστον  των μαθητών που παίζουν βιολί, παίζουν μόνο βιολί.
των μαθητών που παίζουν βιολί, παίζουν μόνο βιολί. Τουλάχιστον
Τουλάχιστον  των μαθητών που παίζουν πιάνο, παίζουν μόνο πιάνο.
των μαθητών που παίζουν πιάνο, παίζουν μόνο πιάνο.Να βρεθεί η μέγιστη δυνατή τιμή του
 .
.
 ή
ή  . Και στις δύο περιπτώσεις προκύπτει
. Και στις δύο περιπτώσεις προκύπτει  , οπότε
, οπότε  .
. , και αφού αυτός είναι πρώτος, ισχύει
, και αφού αυτός είναι πρώτος, ισχύει  , άτοπο.
, άτοπο. , και
, και 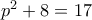 , που είναι πρώτος.
, που είναι πρώτος. (αφού
(αφού  ).
). .
. , τότε το άθροισμα των αριθμών είναι
, τότε το άθροισμα των αριθμών είναι  , άρα ο Βασίλης χάνει.
, άρα ο Βασίλης χάνει.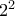 , και έχουμε άθροισμα αριθμών
, και έχουμε άθροισμα αριθμών 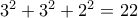 , οπότε ο Βασίλης υποχρεούται να γράψει το
, οπότε ο Βασίλης υποχρεούται να γράψει το  . Το ίδιο κάνει και ο Ανδρέας. Οπότε παίζει ο Βασίλης και το άθροισμα των αριθμών είναι
. Το ίδιο κάνει και ο Ανδρέας. Οπότε παίζει ο Βασίλης και το άθροισμα των αριθμών είναι  , οπότε αναγόμαστε στην προηγούμενη περίπτωση.
, οπότε αναγόμαστε στην προηγούμενη περίπτωση. .
. , και ο Ανδρέας γράφει τον
, και ο Ανδρέας γράφει τον  . Γράφει τότε ο Ανδρέας το
. Γράφει τότε ο Ανδρέας το  είναι το συμμετρικό του
είναι το συμμετρικό του  ως προς την
ως προς την  .
. , άρα τα
, άρα τα 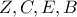 είναι ομοκυκλικά.
είναι ομοκυκλικά. , είναι και
, είναι και 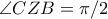 . Ακόμη,
. Ακόμη,  , οπότε αφού
, οπότε αφού  , άρα το
, άρα το 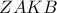 είναι εγγράψιμο.
είναι εγγράψιμο.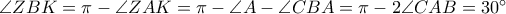 .
. , και
, και  .
.

 .
. , θα προκύψει :
, θα προκύψει :  .
. , άρα προκύπτει
, άρα προκύπτει 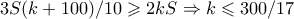 .
. και την επιτυγχάνουμε αν π.χ.
και την επιτυγχάνουμε αν π.χ.  και
και  .
.