Α' Παγκύπριος Διαγωνισμός Επιλογής για BMO/EGMO/IMO 2020

[Demetres]

Αναρτώ εδώ τα χθεσινά θέματα

Πρόβλημα 1: Αν ορίζουμε ως τον μεγαλύτερο ακέραιο αριθμό που είναι μικρότερος ή ίσος με τον . Για παράδειγμα: , και . Να βρείτε το σύνολο των λύσεων της εξίσωσης.




Πρόβλημα 2: Δίνεται τρίγωνο εγγεγραμμένο σε κύκλο . Η κάθετη στην στο τέμνει ξανά τον στο σημείο και η κάθετη στην στο τέμνει ξανά τον στο σημείο . Οι κάθετες από τα σημεία και προς τις ευθείες και αντίστοιχα τέμνονται στο σημείο . Ονομάζουμε το σημείο τομής των ευθειών 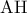και . Αν η διχοτόμος της γωνίας τέμνει το κύκλο στο σημείο , να αποδείξετε ότι η ευθεία διέρχεται από το μέσον του τμήματος .


Πρόβλημα 3: Να βρεθούν όλες οι τριάδες πρώτων αριθμών έτσι ώστε:



(με τον συμβολισμό εννοούμε ότι ο αριθμός είναι διαιρέτης του αριθμού ).


Πρόβλημα 4: Ο Δημήτρης και ο Στέλιος συμφωνούν να παίξουν ένα παιχνίδι με αριθμούς ως εξής:

«Γράφουν εναλλάξ στον πίνακα θετικά τέλεια τετράγωνα με τον όρο ότι ένα τέλειο τετράγωνο μπορεί να γραφεί αρκετές φορές.»

Αν το άθροισμα των αριθμών που είναι γραμμένοι στον πίνακα γίνει μεγαλύτερο του αυτός που έγραψε τον τελευταίο αριθμό χάνει το παιχνίδι.

Αν ο Δημήτρης ξεκινά πρώτος το παιχνίδι να βρείτε ποιος από τους δύο παίκτες έχει στρατηγική νίκης και να εξηγήσετε την στρατηγική.

Επεξεργασία: Διορθώθηκαν (ελπίζω) τα προβλήματα στην εκφώνηση του 2

[ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ]

Πρόβλημα 2: Δίνεται τρίγωνο εγγεγραμμένο σε κύκλο 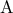. Η κάθετη στην στο τέμνει ξανά τον στο σημείο και η κάθετη στην στο τέμνει ξανά τον στο σημείο . Οι κάθετες από τα σημεία και προς τις ευθείες και αντίστοιχα τέμνονται στο σημείο . Ονομάζουμε το σημείο τομής των ευθειών και . Αν η διχοτόμος της γωνίας τέμνει το κύκλο στο σημείο , να αποδείξετε ότι η ευθεία διέρχεται από το μέσον του τμήματος .

Χρησιμοποιώ λατινικούς χαρακτήρες ( επειδή η εκφώνηση έχει κάποια προβλήματα ''φωτίστε'' πάνω από το κείμενο για να εμφανιστεί το latex)

209.PNG (31.78 KiB) Προβλήθηκε 738 φορές

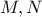Τα είναι αντιδιαμετρικά των άρα .Επίσης ,όμοια και έτσι το είναι παραλληλόγραμμο.Το είναι μέσο του άρα ανήκει στην μεσοκάθετο του στην οποία ανήκει και το άρα μεσοκάθετος του και το ζητούμενο έπεται.

[Ορέστης Λιγνός]

Αναρτώ εδώ τα χθεσινά θέματα

Πρόβλημα 1: Αν ορίζουμε ως τον μεγαλύτερο ακέραιο αριθμό που είναι μικρότερος ή ίσος με τον . Για παράδειγμα: , και . Να βρείτε το σύνολο των λύσεων της εξίσωσης.

Αν το , τότε :

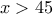i) Αν , τότε το αριστερό μέλος της παραπάνω είναι 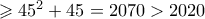, άτοπο.
ii) Αν , τότε το αριστερό μέλος της παραπάνω είναι , άτοπο.

Άρα, , οπότε , και .

Για να ισχύει η πιο πάνω πρέπει και αρκεί .

Ομοίως πράττουμε αν . Τελικά το σύνολο λύσεων της δοσμένης είναι το .

[JimNt.]

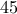4. Ονομάζω καλό έναν θετικό ακέραιο ανν ο παίκτης που φτάνει με την σειρά του στον έχει στρατηγική νίκης. Ελέγχοντας (10 λεπτών δουλειά), από το μέχρι το βλέπουμε ότι καλοί είναι μόνο οι . όμως 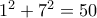, , , . Άρα ο παίζει αναγκαστικά , τώρα όμως νικάει όντως αφού αν ο Β παίξει... ο Α παίζει...., (, , , , , .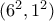