socrates έγραψε: ↑Τετ Φεβ 26, 2020 1:41 am
ΘΕΜΑ 2
Έστω

και

τα ύψη οξυγωνίου τριγώνου

Δύο διαφορετικοί κύκλοι που διέρχονται από τα σημεία

και

εφάπτονται στην ευθεία

στα σημεία

και

έτσι ώστε το

να βρίσκεται ανάμεσα στα

και

Να αποδείξετε ότι οι ευθείες

και

τέμνονται σε σημείο του περιγεγραμμένου κύκλου του τριγώνου

Κομψή η λύση του Πρόδρομου.
Παραθέτω μια διαφορετική (για να έχουμε μία ακόμα και μόνο).Με αυτή τη λύση ανακαλύπτουμε και κάποιες άλλες ιδιότητες του σχήματος (τις τονίζω στο τέλος).
Θα χρησιμοποιώ χώρις αναφορά το θεώρημα ότι 2 σημεία και οι αντίστροφες εικόνες τους ορίζουν εγγράψιμο τετράπλευρο.
Παίρνω αντιστροφή κέντρου

και ακτίνας

. Τότε:
Τα

στέλνονται στα

αντίστοιχα λόγω του εγγράψιμου

. Ο περίκυκλος του

στέλνεται σε ευθεία που εφάπτεται στην αντίστροφη εικόνα της

δηλαδή τον περίκυκλο του

και διέρχεται από το αντίστροφο του

δηλαδή το

.
Αν
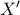
το αντίστροφο του

, τότε αν η

τέμνει τον περίκυκλο του

στο

,τότε

το αντίστροφο του

, άρα

. Άρα η

εφάπτεται του περίκυκλου του

. Ομοίως η

εφάπτεται στον ίδιο κύκλο. Άρα το

αρμονικό. Οπότε η

αρμονική δέσμη όπου

η εφαπτομένη στο

στον περίκυκλο του

. Όμως

και άρα

μέσο του

. Εφόσον το

ανήκει στον ριζικό άξονα των περικύκλων των τριγώνων

έπεται ότι το

είναι το κέντρο του εγγραψίμου

. Από εδώ έπεται ότι τα τρίγωνα

έχουν κοινά ορθόκεντρα. Το σημείο Miquel του

είναι ένα σημείο το οποίο βρίσκεται στην τομή της

με την εκ του

κάθετη προς την

καθώς

η τομή των διαγωνίων και

η τομή δύο απέναντι πλευρών. Άρα αυτό το σημείο είναι το

και άρα

,

,

συντρέχουν.
Αν

η τομή της

με τον περίκυκλο, θα δείξω ότι
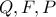
συνευθειακά ή ισοδύναμα από την αντιστροφή ότι

εγγράψιμο όπου

το αντίστροφο του

που ταυτίζεται με την τομή της
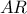
με την

.

άρα

. Τότε

ως εντός εκτός και απί ταυτά.
Τότε

και το ζητούμενο έπεται( στις ισότητες των γωνίων χρησιμοποίησα το εγγράψιμο

).
Ελπίζω να μην τα θαλάσσωσα διότι χάθηκα λίγο στην πολυπλοκότητα του σχήματος.
Ας δούμε τώρα τι βγήκε από εδώ:
i) Τα τρίγωνα

έχουν κοινό ορθόκεντρο.
ii)

εγγράψιμο
iii)

μέσο του

(στο τέλος είδα πιο απλό τρόπο απόδειξης αυτού κατευθείαν με ριζικούς άξονες).
Αν έχει κάποιος όρεξη ας ελέγξει πρώτα την ορθότητα των όσων γράφω και ας προσθέσει και άλλα!

 και
και  τα ύψη οξυγωνίου τριγώνου
τα ύψη οξυγωνίου τριγώνου  Δύο διαφορετικοί κύκλοι που διέρχονται από τα σημεία
Δύο διαφορετικοί κύκλοι που διέρχονται από τα σημεία  και
και  εφάπτονται στην ευθεία
εφάπτονται στην ευθεία  στα σημεία
στα σημεία  και
και  έτσι ώστε το
έτσι ώστε το  να βρίσκεται ανάμεσα στα
να βρίσκεται ανάμεσα στα  και
και  Να αποδείξετε ότι οι ευθείες
Να αποδείξετε ότι οι ευθείες  και
και  τέμνονται σε σημείο του περιγεγραμμένου κύκλου του τριγώνου
τέμνονται σε σημείο του περιγεγραμμένου κύκλου του τριγώνου 
 ,
,  ,
,  είναι τέτοιοι ώστε
είναι τέτοιοι ώστε  Να δείξετε ότι
Να δείξετε ότι 
 παιδιά. Κάθε παιδί έχει τουλάχιστον μια καραμέλα. Σε κάθε γύρο δίνονται επιπλέον καραμέλες σε κάποια από τα παιδιά σύμφωνα με τον κανόνα:
παιδιά. Κάθε παιδί έχει τουλάχιστον μια καραμέλα. Σε κάθε γύρο δίνονται επιπλέον καραμέλες σε κάποια από τα παιδιά σύμφωνα με τον κανόνα:  κάθε παιδί με πλήθος από καραμέλες που είναι αριθμός σχετικά πρώτος με τον
κάθε παιδί με πλήθος από καραμέλες που είναι αριθμός σχετικά πρώτος με τον  παίρνει μία καραμέλα.
παίρνει μία καραμέλα. 
 χρηστικός , θα είναι
χρηστικός , θα είναι  .Έστω προς άτοπο ότι ο
.Έστω προς άτοπο ότι ο  .Επειδή είναι περιττός και όχι πολλαπλάσιο του
.Επειδή είναι περιττός και όχι πολλαπλάσιο του  θα γράφεται στην μορφή
θα γράφεται στην μορφή  .
. .
.

 .Πρέπει
.Πρέπει 
 άρτιος τότε
άρτιος τότε  περιττός με
περιττός με 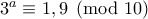 και
και  άρα δεν μπορεί
άρα δεν μπορεί  και
και  άρα δεν μπορεί
άρα δεν μπορεί  να λήγει σε
να λήγει σε  και το ζητούμενο έπεται.
και το ζητούμενο έπεται. ως την τομή του
ως την τομή του  με την
με την  με
με το ορθόκεντρο του
το ορθόκεντρο του  .Είναι
.Είναι  άρα
άρα  άρα το
άρα το  ανήκει στον
ανήκει στον  και μένει να αποδείξουμε πως η
και μένει να αποδείξουμε πως η  .Πράγματι
.Πράγματι  .Άρα
.Άρα  και το ζητούμενο έπεται (
και το ζητούμενο έπεται ( όμοια τρίγωνα κλπ)
όμοια τρίγωνα κλπ)
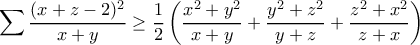



 . Τότε:
. Τότε: στέλνονται στα
στέλνονται στα  αντίστοιχα λόγω του εγγράψιμου
αντίστοιχα λόγω του εγγράψιμου  . Ο περίκυκλος του
. Ο περίκυκλος του  στέλνεται σε ευθεία που εφάπτεται στην αντίστροφη εικόνα της
στέλνεται σε ευθεία που εφάπτεται στην αντίστροφη εικόνα της  και διέρχεται από το αντίστροφο του
και διέρχεται από το αντίστροφο του 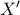 το αντίστροφο του
το αντίστροφο του  , τότε αν η
, τότε αν η  τέμνει τον περίκυκλο του
τέμνει τον περίκυκλο του  ,τότε
,τότε  . Άρα η
. Άρα η  εφάπτεται του περίκυκλου του
εφάπτεται του περίκυκλου του  εφάπτεται στον ίδιο κύκλο. Άρα το
εφάπτεται στον ίδιο κύκλο. Άρα το  αρμονικό. Οπότε η
αρμονικό. Οπότε η  αρμονική δέσμη όπου
αρμονική δέσμη όπου  η εφαπτομένη στο
η εφαπτομένη στο  και άρα
και άρα  . Εφόσον το
. Εφόσον το  έπεται ότι το
έπεται ότι το  . Από εδώ έπεται ότι τα τρίγωνα
. Από εδώ έπεται ότι τα τρίγωνα  έχουν κοινά ορθόκεντρα. Το σημείο Miquel του
έχουν κοινά ορθόκεντρα. Το σημείο Miquel του  με την εκ του
με την εκ του  και άρα
και άρα  ,
,  ,
,  συντρέχουν.
συντρέχουν.  η τομή της
η τομή της  με τον περίκυκλο, θα δείξω ότι
με τον περίκυκλο, θα δείξω ότι 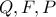 συνευθειακά ή ισοδύναμα από την αντιστροφή ότι
συνευθειακά ή ισοδύναμα από την αντιστροφή ότι  εγγράψιμο όπου
εγγράψιμο όπου  το αντίστροφο του
το αντίστροφο του 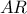 με την
με την  άρα
άρα  . Τότε
. Τότε  ως εντός εκτός και απί ταυτά.
ως εντός εκτός και απί ταυτά.  και το ζητούμενο έπεται( στις ισότητες των γωνίων χρησιμοποίησα το εγγράψιμο
και το ζητούμενο έπεται( στις ισότητες των γωνίων χρησιμοποίησα το εγγράψιμο  ).
).  έχουν κοινό ορθόκεντρο.
έχουν κοινό ορθόκεντρο. εγγράψιμο
εγγράψιμο (στον
(στον  -οστό γύρο).Εξετάζουμε το
-οστό γύρο).Εξετάζουμε το  .
. .
. είτε πέφτει κατά
είτε πέφτει κατά  είτε μένει σταθερό.
είτε μένει σταθερό. για κάποιο
για κάποιο  για κάποιο
για κάποιο  .
. θα έχει κάποιον πρώτο διαιρέτη
θα έχει κάποιον πρώτο διαιρέτη  .Για
.Για  για κατάλληλα μεγάλο
για κατάλληλα μεγάλο  φτάνουμε σε άτοπο.
φτάνουμε σε άτοπο. .
. από όπου στον επόμενο γύρο θα πέσει στην τιμή
από όπου στον επόμενο γύρο θα πέσει στην τιμή  όπου και θα κολλήσει.
όπου και θα κολλήσει. είτε
είτε  καραμέλες,όπου
καραμέλες,όπου  ένας κατάλληλα μεγάλος γύρος .
ένας κατάλληλα μεγάλος γύρος . στη διάμεσο
στη διάμεσο  -οπότε το ορθόκεντρο είναι το
-οπότε το ορθόκεντρο είναι το  .Από
.Από  είναι
είναι  .Είναι
.Είναι  από όπου έπεται το ζητούμενο.
από όπου έπεται το ζητούμενο.
 οπου
οπου  Απο AM-HM η μικροτερη τιμη του a+b+c ειναι 9/2 αρα
Απο AM-HM η μικροτερη τιμη του a+b+c ειναι 9/2 αρα  δηλαδη ισχυει
δηλαδη ισχυει  . Αυτος ο τροπς εχει καποιο λαθος??
. Αυτος ο τροπς εχει καποιο λαθος??