Μαθηματική Ολυμπιάδα Μόσχας 2020 (8η τάξη)

[Al.Koutsouridis]

LXXXIII Μαθηματική Ολυμπιάδα Μόσχας
Θέματα της 8ης τάξης, 1 Μαρτίου 2020.


Πρόβλημα 1. Ο Τομ έγραψε σε έναν ξύλινο φράχτη την λέξη και ο Γκεκ τον αριθμό . Το πλάτος κάθε γράμματος και ψηφίου είναι εκατοστά και το πλάτος κάθε σανίδας του φράχτη εκατοστά. Μπορεί άραγε ο Γγεκ να χρησιμοποίησε λιγότερες σανίδες από ότι ο Τομ; (Οι σανίδες είναι τοποθετημένες κατακόρυφα, οι λέξεις και οι αριθμοί οριζόντια. Τα ψηφία και τα γράμματα γράφονται ανά ίσα διαστήματα.) (Ντ. Μούχιν, Α.Φεντούλκιν, Ι.Έλμαν)


Πρόβλημα 2. Στην γραφική παράσταση της συνάρτησης 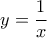ο Μιχάλης σημείωσε με την σειρά όλα τα σημεία με τετμημένες μέχρι να κουραστεί. Ύστερα προσήλθε η Μαρία και χρωμάτισε όλα τα ορθογώνια, μια από τις κορυφές των οποίων είναι ένα σημειωμένο σημείο, άλλη μια η αρχή των αξόνων και οι άλλες δυο βρίσκονται στους άξονες. Έπειτα η δασκάλα ζήτησε από τα παιδιά να υπολογίσουν το εμβαδόν του σχήματος, που αποτελείται από όλα τα σημεία, τα οποία έχουν χρωματιστεί ακριβώς μια φορά. Πόσο προέκυψε; (Ντ. Μούχιν)


Πρόβλημα 3. Δίνεται μη μηδενικός φυσικός αριθμός . Η Βέρα κάνει με αυτόν τις ακόλουθες πράξεις: στην αρχή προσθέτει συνέχεια το μέχρι, ο αριθμός που προκύπτει να διαιρείται με το (αν αρχικά ο αριθμός διαιρείται με το , τότε δε χρειάζεται να προστεθεί τίποτα). Τον αριθμό που προκύπτει η Βέρα τον διαιρεί με το . Στη συνέχεια κάνει τις ίδιες πράξεις με τον καινούργιο αριθμό κ.ο.κ . Από ποιους αριθμούς με αυτές τις πράξεις δεν μπορεί να προκύψει ο ; (Α.Σαλάμοβα)


Πρόβλημα 4. Σε ένα πρωτάθλημα πετοσφαίρισης συμμετέχουν ομάδες. Μετά από ότι κάθε ομάδα έπαιξε με κάθε άλλη από μια φορά, προέκυψε το σύνολο των βαθμών όλων των ομάδων να είναι διαφορετικό. Μετά από ότι κάθε ομάδα έπαιξε με κάθε άλλη για δεύτερη φορά, το σύνολο των βαθμών όλων τον ομάδων προέκυψε να είναι το ίδιο. Στην πετοσφαίριση μια ομάδα για νίκη κερδίζει βαθμούς, για ισοπαλία βαθμό, για ήττα βαθμούς. Είναι άραγε αληθές, ότι θα βρεθούν δυο ομάδες, που κέρδισε η μια την άλλη από μια φορά; (Μπ.Φρένκιν, Α.Ζασλάβσκϊι)


Πρόβλημα 5. Δίνεται τραπέζιο με βάσεις και . Η κάθετος από το σημείο προς την πλευρά , διέρχεται από το μέσο της διαγώνιου και η κάθετος από το σημείο προς την πλευρά , διέρχεται από το μέσο της διαγώνιου . Να αποδείξετε ότι το τραπέζιο είναι ισοσκελές. (Α.Ντολεντόνοκ)


Πρόβλημα 6. Η Πολίνα έχει μια τράπουλα των καρτών ( σειρές των καρτών η κάθε μία). Διαλέγει από την τράπουλα τις μισές κάρτες, όποιες θέλει, και τις δίνει στην Βασιλίσσα, το δεύτερο μισό της τράπουλας το κρατάει για τον εαυτό της. Ύστερα σε κάθε κίνηση οι παίχτριες με την σειρά «ανοίγουν» από μια κάρτα τις επιλογής τους (ο αντίπαλος βλέπει την σειρά και τιμή της ανοιχτής κάρτας), ξεκινώντας με την Πολίνα. Αν ως απάντηση στην κίνηση της Πολίνας η Βασιλίσσα μπορεί να ανοίξει κάρτα της ίδιας σειράς ή ίδιας τιμής, τότε η Βασιλίσσα κερδίζει ένα βαθμό. Ποιος είναι ο μέγιστος αριθμός βαθμών, που εγγυημένα μπορεί να κερδίσει η Βασιλίσσα; (Μ.Εβδοκίμοβ)


Πηγή

[ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ]

Πρόβλημα 2. Στην γραφική παράσταση της συνάρτησης ο Μιχάλης σημείωσε με την σειρά όλα τα σημεία με τετμημένες μέχρι να κουραστεί. Ύστερα προσήλθε η Μαρία και χρωμάτισε όλα τα ορθογώνια, μια από τις κορυφές των οποίων είναι ένα σημειωμένο σημείο, άλλη μια η αρχή των αξόνων και οι άλλες δυο βρίσκονται στους άξονες. Έπειτα η δασκάλα ζήτησε από τα παιδιά να υπολογίσουν το εμβαδόν του σχήματος, που αποτελείται από όλα τα σημεία, τα οποία έχουν χρωματιστεί ακριβώς μια φορά. Πόσο προέκυψε; (Ντ. Μούχιν)

278.PNG (11.49 KiB) Προβλήθηκε 438 φορές

Αρχικά βρίσκω το εμβαδό της περιοχής η οποία έχει χρωματιστεί ακριβώς μία φορά ανάμεσα στο διάστημα συναρτήσει του .
Είναι και
άρα
Έτσι αν σταμάτησε στον προέκυψε
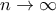Όταν τότε