Να προσδιορίσετε όλα τα ζεύγη
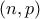 θετικών ακεραίων, όπου
θετικών ακεραίων, όπου  πρώτος, τα οποία ικανοποιούν την εξίσωση
πρώτος, τα οποία ικανοποιούν την εξίσωση 
ΘΕΜΑ 2
Το τετράπλευρο
 είναι εγγράψιμο σε κύκλο και ισχύει
είναι εγγράψιμο σε κύκλο και ισχύει  . Το σημείο
. Το σημείο  βρίσκεται στην
βρίσκεται στην  έτσι ώστε
έτσι ώστε  , το σημείο
, το σημείο  στην
στην 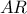 ώστε
ώστε  . Επιπλέον,
. Επιπλέον, 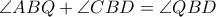 και η
και η  τέμνει την
τέμνει την  στο
στο  .
.Να βρείτε το μέτρο της γωνίας

ΘΕΜΑ 3
Η Άννα και η Βασιλική παίζουν το παρακάτω παιχνίδι:
Στο τραπέζι υπάρχουν
 κέρματα και οι δύο φίλες παίρνουν εναλλάξ κάποια από αυτά.
κέρματα και οι δύο φίλες παίρνουν εναλλάξ κάποια από αυτά. Μπορούν να πάρουν το πολύ
 κέρματα κάθε φορά, όπου
κέρματα κάθε φορά, όπου  το πλήθος των κερμάτων που υπάρχουν τότε στο τραπέζι, αλλά τουλάχιστον ένα. Όποια πάρει τα τελευταία (ή το τελευταίο) κέρμα κερδίζει.
το πλήθος των κερμάτων που υπάρχουν τότε στο τραπέζι, αλλά τουλάχιστον ένα. Όποια πάρει τα τελευταία (ή το τελευταίο) κέρμα κερδίζει. Αν πρώτη παίζει η Άννα, ποια από τις δύο φίλες έχει στρατηγική νίκης;
ΘΕΜΑ 4
Αν
 θετικοί πραγματικοί αριθμοί, να δείξετε ότι:
θετικοί πραγματικοί αριθμοί, να δείξετε ότι:

 ,πλην
,πλην  και στα δύο μέλη και καταλήγει στην
και στα δύο μέλη και καταλήγει στην  που ισχύει από
που ισχύει από  (είναι πχ.
(είναι πχ. )
) αδύνατο
αδύνατο τότε το
τότε το  και
και 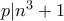 άρα
άρα  .Από το μικρο θεώρημα του Fermat αν
.Από το μικρο θεώρημα του Fermat αν  τότε αυτό είναι άτοπο. Αν όμως
τότε αυτό είναι άτοπο. Αν όμως  όμως
όμως  άρα άτοπο και αυτό. Δηλαδή δεν υπάρχει λύση στους θετικούς ακεραίους
άρα άτοπο και αυτό. Δηλαδή δεν υπάρχει λύση στους θετικούς ακεραίους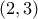 η
η 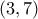 .
.
 προφανώς δεν έχει λύση.
προφανώς δεν έχει λύση.
 , δεν παίρνουμε λύσεις.
, δεν παίρνουμε λύσεις. .
.

 γίνεται μετά από πράξεις:
γίνεται μετά από πράξεις:
 πρέπει να είναι τέλειο τετράγωνο περιττού αριθμού.
πρέπει να είναι τέλειο τετράγωνο περιττού αριθμού. :
:
 .
. , οπότε προκύπτει το μοναδικό ζεύγος
, οπότε προκύπτει το μοναδικό ζεύγος  .
. 
 Αύριο η λύση αν δεν απαντηθεί μέχρι τότε.
Αύριο η λύση αν δεν απαντηθεί μέχρι τότε. ,
,  , και
, και  .
.  .
. , που δίνει άμεσα ότι
, που δίνει άμεσα ότι  . Τότε, είναι
. Τότε, είναι  .
. μέσο
μέσο  και
και  . Έστω ακόμη
. Έστω ακόμη  σημείο της
σημείο της  με
με  .
. .
.  εγγράψιμο. Οπότε,
εγγράψιμο. Οπότε,  , οπότε
, οπότε  και
και  . Επίσης
. Επίσης 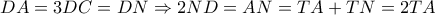 , άρα
, άρα  .
.
 .
. με
με  . Έστω ακόμη,
. Έστω ακόμη,  και
και  .
. , άρα
, άρα  . Έστω τώρα
. Έστω τώρα  . Τότε, είναι
. Τότε, είναι  , άρα τα
, άρα τα  είναι ίσα.
είναι ίσα. . Το
. Το  είναι εγγράψιμο, άρα από τον Ισχυρισμό 2,
είναι εγγράψιμο, άρα από τον Ισχυρισμό 2,  , οπότε
, οπότε  , με
, με  , οπότε
, οπότε  , οπότε τα
, οπότε τα  είναι συνευθειακά.
είναι συνευθειακά. με διατέμνουσα
με διατέμνουσα  προκύπτει ότι (αφού
προκύπτει ότι (αφού  ),
),  , οπότε
, οπότε 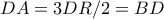 , δηλαδή το
, δηλαδή το  είναι ισοσκελές!
είναι ισοσκελές! (
( ) είναι ισοσκελές τραπέζιο, οπότε
) είναι ισοσκελές τραπέζιο, οπότε 
 , οπότε
, οπότε  .
. και
και 
 (1)
(1)
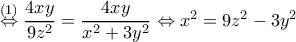 (i)
(i) (2)
(2)

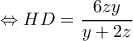 (3)
(3)
 και η γενίκαυση του πυθαγωρίου θεωρήματος στο
και η γενίκαυση του πυθαγωρίου θεωρήματος στο  δίνει
δίνει  (ii)
(ii)
 ΚΑΙ αφού
ΚΑΙ αφού  διχοτόμος της
διχοτόμος της  είναι
είναι 
 τέμνει την
τέμνει την  στο
στο  Με τους συμβολισμούς του σχήματος έχω:
Με τους συμβολισμούς του σχήματος έχω: 



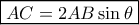




 στο τρίγωνο
στο τρίγωνο  απ' όπου
απ' όπου 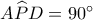
 , οι οποίοι είναι πάντα περιττοί.
, οι οποίοι είναι πάντα περιττοί. .
. ότι αν ο
ότι αν ο  ,
,  . Τότε η Άννα παίρνει το πολύ δύο νομίσματα, οπότε η Βασιλική παίρνει τα υπόλοιπα και κερδίζει.
. Τότε η Άννα παίρνει το πολύ δύο νομίσματα, οπότε η Βασιλική παίρνει τα υπόλοιπα και κερδίζει. .
. η Άννα ως πρώτη μπορεί να πάρει το πολύ
η Άννα ως πρώτη μπορεί να πάρει το πολύ  , δηλαδή μένουν τουλάχιστον
, δηλαδή μένουν τουλάχιστον  νομίσματα.
νομίσματα. νομίσματα μετά την πρώτη κίνηση της Άννας με
νομίσματα μετά την πρώτη κίνηση της Άννας με  .
. άρτιος, η Βασιλική μπορεί να πάρει το πολύ
άρτιος, η Βασιλική μπορεί να πάρει το πολύ 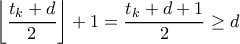 νομίσματα, αφού
νομίσματα, αφού  .
. νομίσματα, αφού
νομίσματα, αφού  .
.