Cyberspace Mathematical Competition 2020

#1

Φέτος διεξήχθει για πρώτη φορά ο διαγωνισμός Cyberspace Mathematical Competition. Ελλάδα και Κύπρος λάβαμε μέρος με πλήρεις ομάδες των 8 ατόμων εκ των οποίων τα 2 ήταν απαραίτητα κορίτσια.

Ο διαγωνισμός έλαβε μέρος τη Δευτέρα 13/7 και Τρίτη 14/7. Κάθε μέρα αποτελείτο από 4 προβλήματα το πρώτο εκ των οποίων ήταν «αισθητά ευκολότερο» από τα προβλήματα της ΙΜΟ ενώ τα άλλα τρία ήταν ανάλογου επιπέδου με αυτά της ΙΜΟ. Σύντομα θα έχουμε νέα για το πως τα πήγαν τα παιδιά. Παραθέτω τα προβλήματα:

Πρόβλημα 1. Θεωρούμε ένα $n \times n$ τετράγωνο που χωρίζεται σε μοναδιαία τετράγωνα με τον συνήθη τρόπο. Η κύρια διαγώνιος του πίνακα είναι τα

μοναδιαία τετράγωνα στην κύρια διαγώνιο του πίνακα από άνω αριστερά μέχρι κάτω δεξιά. Έχουμε απεριόριστη ποσότητα από πλακίδια της μορφής:

: fig_problem1.png (355 Ψηφιολέξεις) Προβλήθηκε 1749 φορές

Τα πλακίδια μπορούν να περιστραφούν. Θέλουμε να τοποθετήσουμε τα πλακίδια στον πίνακα ώστε κάθε πλακίδιο να καλύπτει ακριβώς τρία μοναδιαία τετράγωνα ώστε να μην υπάρχει ζεύγος πλακιδίων που να επικαλύπτονται, κάθε μοναδιαίο τετράγωνο στην κύρια διαγώνιο του πίνακα να μην καλύπτεται από πλακίδιο και όλα τα άλλα μοναδιαία τετράγωνα του πίνακα να καλύπτονται ακριβώς από μία φορά. Για ποια $n\geq 2$ είναι δυνατό να επιτευχθεί αυτό;

Πρόβλημα 2. Έστω f(x)=3x^2+1

. Να δειχθεί ότι για κάθε θετικό ακέραιο

, το γινόμενο

$\displaystyle f(1) f(2) \cdots f(n)$

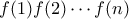
έχει το πολύ

πρώτους διαιρέτες που είναι διαφορετικοί ανά δύο.

Πρόβλημα 3. Έστω τρίγωνο ABC

τέτοιο ώστε AB > BC

και έστω

μεταβλητό σημείο στο εσωτερικό του ευθύγραμμου τμήματος

. Έστω

το σημείο στον περιγεγραμμένο κύκλο του τριγώνου ABC

ώστε $\angle BAE = \angle DAC$ και επιπλέον τα A,E

να βρίσκονται σε διαφορετικά ημιεπίπεδα που ορίζει η

. Έστω

το έγκεντρο του τριγώνου ABD

και έστω

το έγκεντρο του τριγώνου ACE

. Να δειχθεί ότι η ευθεία

περνάει από ένα σταθερό σημείο, το οποίο είναι ανεξάρτητο του

.

Πρόβλημα 4. Έστω περιττός θετικός ακέραιος

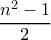. Κάποια τετράγωνα μιας $n \times n$ σκακιέρας έχουν βαφτεί πράσινα. Δίνεται ότι ο βασιλιάς μπορεί να κινηθεί από οποιοδήποτε πράσινο τετράγωνο της σκακιέρας σε οποιοδήποτε άλλο πράσινο τετράγωνο της σκακιέρας. Να αποδειχθεί ότι μπορεί πάντα να το κάνει αυτό το πολύ σε $\displaystyle \frac{n^2 - 1}{2}$ κινήσεις. (Σε μία κίνηση, ο βασιλιάς μπορεί να μετακινηθεί από ένα τετράγωνο σε ένα άλλο αν και μόνο αν τα δύο τετράγωνα έχουν κοινή πλευρά ή κοινή κορυφή.)

Πρόβλημα 5. Σε έναν πίνακα είναι γραμμένοι 2020

θετικοί ακέραιοι. Κάθε ένα λεπτό ο Zuming σβήνει δύο από τους αριθμούς και τους αντικαθιστά από το άθροισμα, τη διαφορά, το γινόμενο ή το πηλίκο τους. Π.χ. αν ο Zuming σβήσει τους

και

, μπορεί να τους αντικαταστήσει με ένα από τους αριθμούς του συνόλου $\{6+3, 6-3, 3-6, 6\times 3, 6\div 3, 3\div 6\} = \{9, 3, -3, 18, 2, \frac{1}{2}\}$ . Μετά από 2019 λεπτά μένει μόνο ένας αριθμός γραμμένος στον πίνακα, ο

. Να αποδειχθεί ότι θα μπορούσε ο Zuming, ακολουθώντας τους ίδιους κανόνες και ξεκινώντας από τους ίδιους 2020

ακεραίους, να γράψει στο τέλος τον αριθμό 2020

.

Πρόβλημα 6. Να βρεθούν όλοι οι ακέραιοι $n \geq 3$ για τους οποίους η ακόλουθη πρόταση είναι αληθής: Αν το $\mathcal{P}$ είναι ένα κυρτό

-γωνο τέτοιο ώστε n-1

από τις πλευρές του έχουν όλες το ίδιο μήκος και n-1

από τις γωνιές του είναι όλες ίσες μεταξύ τους, τότε το $\mathcal{P}$ είναι ένα κανονικό πολύγωνο.

Πρόβλημα 7. Κάθε ένα από τα n^2

κελιά ενός $n \times n$ πλέγματος χρωματίζεται είτε μαύρο είτε άσπρο. Έστω a_i

το πλήθος των άσπρων κελιών στην οριζόντια σειρά

και

το πλήθος των μαύρων κελιών στην κάθετη στήλη

. Να υπολογιστεί η μέγιστη δυνατή τιμή του $\displaystyle \sum_{i = 1}^n a_i b_i$ που μπορεί να προκύψει.

Πρόβλημα 8. Έστω $a_1, a_2, \ldots \,$ μια άπειρη ακολουθία θετικών πραγματικών αριθμών τέτοια ώστε για κάθε θετικό ακέραιο

να έχουμε

$\displaystyle \frac{a_1 + a_2 + \cdots + a_n}{n} \ge \sqrt{\frac{a_1^2 + a_2^2 + \cdots + a_{n+1}^2}{n+1}}.$

Να αποδειχθεί ότι η ακολουθία $a_1, a_2, \ldots \,$ είναι σταθερή.

Τσιαλας Νικολαος · #2

Οι βαθμολογίες!

https://artofproblemsolving.com/contest ... aderboards

MAnTH05 · #3

Επαναφέρω το θέμα για να δώσω τη λύση μου στο Πρόβλημα 3.

Ας θεωρήσουμε ότι η ευθεία

τέμνει την προέκταση της πλευράς

σε σημείο

. Θα δείξουμε ότι τα σημεία

,

και

είναι συνευθειακά.

Ισχύει $\angle BAE = \angle DAC = \phi$

Αρχικά παρατηρούμε πως τα τρίγωνα ABD

και

είναι όμοια, διότι 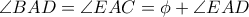$\angle BAD = \angle EAC = \phi + \angle EAD$
και $\angle ABC = \angle AEC$ (ως εγγεγραμμένες στο τόξο

) άρα $\angle ABD = \angle AEC$ .

Επομένως $\angle AID = \angle AJC = 90^{\circ} + \frac{\angle ABC}{2}$ (1)

και $\frac{\angle ADB}{2} = \frac{\angle ACE}{2}$ (2)

Από τις σχέσεις (1)

και

συμπεραίνουμε ότι και τα τρίγωνα AID

και

είναι όμοια.

Ας θεωρήσουμε μία σπειροειδή ομοιότητα (σύνθεση στροφής και ομοιοθεσίας) που στέλνει το τρίγωνο ABD

στο τρίγωνο AEP

Ο μετασχηματισμός αυτός, θα στείλει το τρίγωνο AID

στο τρίγωνο AJP

. Επομένως $\angle ADI = \angle APJ$

Συνεπώς τα τρίγωνα AJP

και

είναι όμοια, άρα $\angle ACJ = \angle APJ$ (3)

Από τη σχέση (3)

προκύπτει ότι το τετράπλευρο AJCP

είναι εγγράψιμο.

Επομένως $\angle APD = 90^{\circ} + \frac{\angle ABC}{2}$ (4)

Η σχέση

δίνει ότι και το τετράπλευρο AIDP

είναι εγγράψιμο, άρα $\angle API = \angle ADI$

Συμπεραίνουμε, λοιπόν ότι $\angle API = \angle ADI =\angle APJ = \theta$
Το ζητούμενο έπεται. $\square$

Cyberspace Mathematical Competition 2020

Cyberspace Mathematical Competition 2020

Re: Cyberspace Mathematical Competition 2020

Re: Cyberspace Mathematical Competition 2020

Μέλη σε σύνδεση