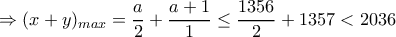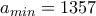Θέματα της 1ης φάσης για την 6η τάξη
1. Μια πόλη έχει την μορφή ενός τετραγωνισμένου σχήματος. Οι γραμμές είναι οι δρόμοι και τα τετράγωνα είναι τα οικοδομικά τετράγωνα. Ο Κώστας και η Όλγα ξεκίνησαν από την διασταύρωση
 προς την ίδια διεύθυνση και στην συνέχεια ο καθένας τους σε κάθε διασταύρωση είτε έστριβε (δεξιά ή αριστερά), είτε προχωρούσε ευθεία μπροστά. Ο Κώστας έστριψε
προς την ίδια διεύθυνση και στην συνέχεια ο καθένας τους σε κάθε διασταύρωση είτε έστριβε (δεξιά ή αριστερά), είτε προχωρούσε ευθεία μπροστά. Ο Κώστας έστριψε  φορές αριστερά,
φορές αριστερά,  φορές δεξιά και
φορές δεξιά και  φορές προχώρησε ευθεία. Η Όλγα έστριψε
φορές προχώρησε ευθεία. Η Όλγα έστριψε  φορές δεξιά,
φορές δεξιά,  φορές αριστερά και
φορές αριστερά και  φορές προχώρησε ευθεία. Θα μπορούσαν άραγε, ως αποτέλεσμα της κίνησής τους και οι δυο τους να βρεθούν στην ίδια διασταύρωση
φορές προχώρησε ευθεία. Θα μπορούσαν άραγε, ως αποτέλεσμα της κίνησής τους και οι δυο τους να βρεθούν στην ίδια διασταύρωση  ;
;2. Σε ένα μοναστήρι κάθε μοναχός είναι είτε εξομολογούμενος, είτε εξομολόγος. Στη συζήτηση με εξομολογούμενο κάθε άτομο λέει πάντα την αλήθεια και στη συζήτηση με τον εξομολόγο, ψεύδεται. Ακριβώς έναν από τους μοναχούς τον λένε Ψευτούλη. Μια φορά ο μοναχός
 είπε στον μοναχό
είπε στον μοναχό  : «Εν τέλη ο Ψευτούλης είναι εξομολογούμενος». Ύστερα ο μοναχός
: «Εν τέλη ο Ψευτούλης είναι εξομολογούμενος». Ύστερα ο μοναχός  είπε στον
είπε στον  : “Ο Ψευτούλης είναι εξομολόγος». Στο τέλος ο
: “Ο Ψευτούλης είναι εξομολόγος». Στο τέλος ο  είπε στον μοναχό
είπε στον μοναχό  : «Ο Ψευτούλης είμαι εγώ!!». Μπορεί άραγε ο μοναχός
: «Ο Ψευτούλης είμαι εγώ!!». Μπορεί άραγε ο μοναχός  να είναι εξομολογούμενος;
να είναι εξομολογούμενος;3. Ένα τετράγωνο διαστάσεων
 είναι κομμένο σε σχήματα της μορφής (τα σχήματα μπορεί να έχουν περιστραφεί και αναποδογυριστεί). Για κάθε γραμμή κελιών (οριζόντια ή κάθετη) σημειώθηκε: κελιά πόσων σχημάτων αυτή περιέχει. Το άθροισμα αυτών τον διακοσίων αριθμών προέκυψε ίσο με
είναι κομμένο σε σχήματα της μορφής (τα σχήματα μπορεί να έχουν περιστραφεί και αναποδογυριστεί). Για κάθε γραμμή κελιών (οριζόντια ή κάθετη) σημειώθηκε: κελιά πόσων σχημάτων αυτή περιέχει. Το άθροισμα αυτών τον διακοσίων αριθμών προέκυψε ίσο με 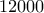 . Πόσα μεταξύ των σχημάτων είναι τετράγωνα; Μη ξεχάσετε να δικαιολογήσετε την απάντηση. (Για παράδειγμα στο σχήμα φαίνονται οι σημειωμένοι αριθμοί των γραμμών για ένα ορθογώνιο
. Πόσα μεταξύ των σχημάτων είναι τετράγωνα; Μη ξεχάσετε να δικαιολογήσετε την απάντηση. (Για παράδειγμα στο σχήμα φαίνονται οι σημειωμένοι αριθμοί των γραμμών για ένα ορθογώνιο  .)
.)
4. Από τους φυσικούς αριθμούς
 και
και  διαλέξαμε από έναν διαιρέτη τους. Το άθροισμά των διαιρετών προέκυψε ίσο με
διαλέξαμε από έναν διαιρέτη τους. Το άθροισμά των διαιρετών προέκυψε ίσο με 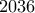 . Ποια είναι η ελάχιστη τιμή που μπορεί να έχει ο αριθμός
. Ποια είναι η ελάχιστη τιμή που μπορεί να έχει ο αριθμός  ;
;Πηγή

 ο διαιρέτης του
ο διαιρέτης του  ο διαιρέτης του
ο διαιρέτης του  .
. και
και 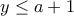 . Προσθέτοντάς τες κατά μέλη λαμβάνουμε
. Προσθέτοντάς τες κατά μέλη λαμβάνουμε 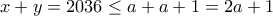 που δίνει
που δίνει  που δίνει
που δίνει  που δίνει
που δίνει  . Επομένως
. Επομένως 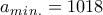 .
. , τότε
, τότε  . Εξέτασε τους διαιρέτες του
. Εξέτασε τους διαιρέτες του  , δίνει κάποιος ως άθροισμα μαζί με τους διαιρέτες του
, δίνει κάποιος ως άθροισμα μαζί με τους διαιρέτες του  τον αριθμό
τον αριθμό 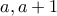 των
των  και
και 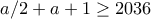 που δίνει
που δίνει 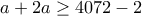 που δίνει
που δίνει 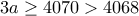 που δίνει
που δίνει 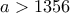 που δίνει
που δίνει  . Πράγματι για
. Πράγματι για 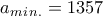 θα έχουμε τους διαιρέτες
θα έχουμε τους διαιρέτες 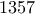 και
και  με άθροισμα
με άθροισμα 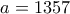 τότε παίρνουμε ως διαιρέτη του
τότε παίρνουμε ως διαιρέτη του 
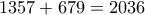
 τότε θεωρούμε τους διαιρέτες
τότε θεωρούμε τους διαιρέτες 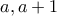 αντίστοιχα.
αντίστοιχα.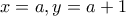 τότε
τότε  αδύνατο
αδύνατο  όπου
όπου 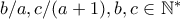 και τουλάχιστον ένας εκ των δύο είναι διαφορετικός του
και τουλάχιστον ένας εκ των δύο είναι διαφορετικός του