Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2021)

[Al.Koutsouridis]

Ανοιχτή Ολυμπιάδα ΦΜΛ 239
Θέματα τάξεων 10-11, 4 Απριλίου 2021


1. Δίνονται διαφορετικοί πρώτοι αριθμοί . Εξετάζουμε το πολυώνυμο , όπου είναι το γινόμενο των πρώτων δοθέντων πρώτων αριθμών. Για ποια αυτό μπορεί να έχει ακέραια ρίζα;


2. Το τρίγωνο με αμβλεία την γωνία είναι εγγεγραμμένο σε κύκλο με κέντρο το σημείο . Ο περιγεγραμμένος κύκλος, με κέντρο , του τριγώνου τέμνει την ευθεία στα σημεία και , την ευθεία στα σημεία και καθώς και την μεσοκάθετο του τμήματος στα σημεία και . Να αποδείξετε, ότι σημεία και καθώς και τα κέντρα των περιγεγραμμένων κύκλων των τριγώνων και 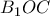είναι ομοκυκλικά.


3. Δυο διαφορετικές ακολουθίες θετικών ακεραίων αριθμών 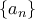και είναι τέτοιες, ώστε σε κάθε μια από αυτές οι δυο πρώτοι όροι είναι πρώτοι μεταξύ τους φυσικοί αριθμοί, μικρότεροι του και κάθε όρος, ξεκινώντας από τον τρίτο, ισούται με το άθροισμα των δυο προηγούμενων. Να αποδείξετε, ότι αν ο διαιρείται με τον , τότε .


4. Οι συμμετροδιάμεσοι οξυγώνιου μη ισοσκελούς τριγώνου τέμνονται στο σημείο και , , είναι τα ύψη του. Να αποδείξετε, ότι μπορούν να κατασκευασθούν ισόπλευρα τρίγωνα , και , που δεν βρίσκονται στο επίπεδο έτσι, ώστε οι ευθείες , και καθώς και η κάθετος από το σημείο προς το επίπεδο να τέμνονται στο ίδιο σημείο.


5. Δίνονται τρεις μιγαδικοί αριθμοί . Να αποδείξετε ότι

,

αν οι παρονομαστές δεν μηδενίζονται.


6. Στο αλφάβητο της φυλής έχει όλο και όλο δυο γράμματα, τα και . Εξάλλου αν σε οποιαδήποτε λέξη τοποθετήσουμε ή διαγράψουμε τον συνδυασμό ή , τότε η σημασία της λέξης δεν αλλάζει. Επιπλέον, αν ανταλλάξουμε μεταξύ τους σε οποιαδήποτε θέση της λέξης τους συνδυασμούς και καθώς και και η σημασία της λέξης δεν αλλάζει. Είναι άραγε αληθές ότι οι λέξεις και έχουν την ίδια σημασία;


7. Στο επίπεδο δίνονται ευθείες, οι οποίες διαμερίζουν το επίπεδο σε μερικά πολυγωνικά χωρία (φραγμένα και μη). Βαθμό ενός τέτοιου χωρίου θα ονομάσουμε το πλήθος των κορυφών στο σύνορό του. Να αποδείξετε ότι το άθροισμα των τετραγώνων των βαθμών όλων των χωρίων δεν υπερβαίνει το .


8. Δυο οποιοιδήποτε κάτοικοι μιας πόλης έχουν άρτιο αριθμό κοινών φίλων σε αυτή την πόλη. Στην μέρα του πολιούχου της πόλης μερικοί κάτοικοι στέλνουν ευχετήριες κάρτες στους φίλους τους. Κάθε κάτοικος με περιττό αριθμό φίλων στέλνει ακριβώς μια κάρτα, κάθε άλλος το πολύ μια. Εξάλλου ο καθένας τους λαμβάνει το πολύ μια ευχητήρια κάρτα. Να αποδείξετε ότι το πλήθος των τρόπων που αυτό μπορεί να συμβεί, είναι περιττό.


Πηγή

[Lymperis Karras]

2. Το τρίγωνο με αμβλεία την γωνία είναι εγγεγραμμένο σε κύκλο με κέντρο το σημείο . Ο περιγεγραμμένος κύκλος, με κέντρο , του τριγώνου τέμνει την ευθεία στα σημεία και , την ευθεία στα σημεία και καθώς και την μεσοκάθετο του τμήματος στα σημεία και . Να αποδείξετε, ότι σημεία και καθώς και τα κέντρα των περιγεγραμμένων κύκλων των τριγώνων και είναι ομοκυκλικά.

Πολύ όμορφη.

Έστω

Είναι

Όμοια είναι και .

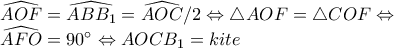
Έχω , άρα το είναι παραλληλλόγραμμο.

Τώρα οι ίσες γωνίες βαίνουν στην κοινή χορδή , άρα .

Αλλά και .

Από το παραλληλλόγραμμο και την μεσοκάθετο της όμως έχουμε ότι .

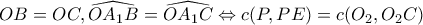Τελικά τα ανήκουν σε κύκλο

FML_2.PNG (109.6 KiB) Προβλήθηκε 545 φορές

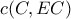
Καταλάθως στο σχήμα έχω αντί για