Θέματα 8ης τάξης για την 2η φάση, 13 Φεβρουαρίου 2022.
1. 10 μαθητές συμμετείχαν σε μια ολυμπιάδα των 11 προβλημάτων. Η βαθμολογία των προβλημάτων γινόταν, μετά τον έλεγχο όλων των γραπτών, με τον εξής κανόνα: αν το πρόβλημα έχει λυθεί από ένα άτομο -4 μόρια, αν έχει λυθεί από 2 άτομα – 2 μόρια, αν από 3 ή 4 άτομα – 1 μόριο, αν περισσότερα από 4 άτομα – 0 μόρια. Να αποδείξετε ότι κάποιοι δυο μαθητές είχαν την ίδια βαθμολογία. (Ο. Ιβάνοβα)
2. Στην πλευρά
 του τριγώνου
του τριγώνου  δίνονται δυο σημεία
δίνονται δυο σημεία  και
και  τέτοια, ώστε
τέτοια, ώστε  . Στο τμήμα
. Στο τμήμα  δίνεται σημείο
δίνεται σημείο  και στο τμήμα
και στο τμήμα  σημείο
σημείο  , εξάλλου
, εξάλλου  και
και  . Οι ημιευθείες
. Οι ημιευθείες  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  . Να αποδείξετε, ότι το μέσο του τμήματος
. Να αποδείξετε, ότι το μέσο του τμήματος  βρίσκεται στην ευθεία
βρίσκεται στην ευθεία  . (Α. Κουζνέτσοβ)
. (Α. Κουζνέτσοβ)3. Να βρείτε όλα τα ζεύγη ακέραιων αριθμών
 , για τα οποία τα
, για τα οποία τα  ,
,  και
και  είναι τέλεια τετράγωνα. (Α. Γκολοβάνοβ)
είναι τέλεια τετράγωνα. (Α. Γκολοβάνοβ)4. Στο τραπέζι βρίσκονται 100 σταθμά διαφορετικών βαρών. Το σταθμό ονομάζεται πετυχημένο, αν το βάρος του είναι ίσο με το άθροισμα των βαρών κάποιων δυο άλλων σταθμών του τραπεζιού. Για ποιο ελάχιστο πλήθος επιτυχημένων σταθμών μπορούμε με βεβαιότητα να εγγυηθούμε, ότι τα βάρυ κάποιων δυο σταθμών διαφέρουν τουλάχιστον κατά τρεις φορές; (Σ. Μπερλόβ)
Καταληκτική αίθουσα
5. Σε μια χώρα υπάρχουν πολλές πόλεις, μεταξύ των οποίων 500 είναι μεγάλες και οι υπόλοιπες μικρές. Μερικα ζεύγη πόλεων είναι συνδεδεμένα με δρόμους έτσι, ώστε από οποιαδήποτε πόλη μπορούμε να μεταβούμε σε οποιαδήποτε άλλη. Υπάρχουν τουλάχιστον 10000 μικρές πόλεις, που συνδέονται με δρόμο τουλάχιστον με μια μεγάλη πόλη. Να αποδείξετε ότι μπορούμε να κλείσουμε μερικούς δρόμους έτσι, ώστε παρ’ όλα αυτά από οποιαδήποτε πόλη να μπορούμε να μεταβούμε σε οποιαδήποτε άλλη και να υπάρχουν πάνω από 9000 πόλεις, από τις οποίες εξέρχεται ένας δρόμος. (Δ. Καρπόβ)
6. Δίνεται ένα παραλληλόγραμμο
 , στο οποίο
, στο οποίο  . Στην επέκταση της διαγώνιου
. Στην επέκταση της διαγώνιου  προς το σημείο
προς το σημείο  δίνεται σημείο
δίνεται σημείο  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
. 7. Δίνεται ένας πρώτος αριθμός
 . Θα ονομάσουμε τον περιττό σύνθετο αριθμό
. Θα ονομάσουμε τον περιττό σύνθετο αριθμό 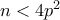 παράξενο, αν για κάθε γνήσιο διαιρέτη του
παράξενο, αν για κάθε γνήσιο διαιρέτη του  τουλάχιστον ένας από τους αριθμούς
τουλάχιστον ένας από τους αριθμούς  ή
ή  επίσης να είναι φυσικός διαιρέτης του
επίσης να είναι φυσικός διαιρέτης του  . Να αποδείξετε ότι το πλήθος των παράξενων αριθμών δεν υπερβαίνει το
. Να αποδείξετε ότι το πλήθος των παράξενων αριθμών δεν υπερβαίνει το  . (Γνήσιος διαιρέτης ενός αριθμού
. (Γνήσιος διαιρέτης ενός αριθμού  ονομάζεται κάθε διαιρέτης του διάφορος του
ονομάζεται κάθε διαιρέτης του διάφορος του  και
και  .)
.)Πηγή: Επίσημη σελίδα της ολυμπιάδας.

 στην
στην  τέμνει την
τέμνει την  στο
στο  Προφανώς οι μοβ γωνίες είναι ίσες όπως και οι κόκκινες.
Προφανώς οι μοβ γωνίες είναι ίσες όπως και οι κόκκινες.  κι επειδή
κι επειδή  θα είναι
θα είναι  οπότε τα τρίγωνα
οπότε τα τρίγωνα  είναι ίσα,
είναι ίσα, δηλαδή το
δηλαδή το  είναι παραλληλόγραμμο και
είναι παραλληλόγραμμο και  μέσο του
μέσο του 
 ,
,  και
και  . Εύκολα προκύπτει ότι
. Εύκολα προκύπτει ότι  (πράγματι,
(πράγματι,  ).
). , είναι
, είναι 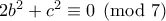 , οπότε εύκολα προκύπτει ότι
, οπότε εύκολα προκύπτει ότι  (αν
(αν  και
και  τέτοιο ώστε
τέτοιο ώστε  , τότε
, τότε  , άρα
, άρα  , άτοπο καθώς το
, άτοπο καθώς το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  ,
, 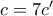 τότε
τότε  , άρα
, άρα  , οπότε αν
, οπότε αν  τότε
τότε  , και συνεχίζοντας όμοια (άπειρη κάθοδος) προκύπτει ότι πρέπει
, και συνεχίζοντας όμοια (άπειρη κάθοδος) προκύπτει ότι πρέπει  , οπότε τελικά και
, οπότε τελικά και  .
. άρα το τετράπλευρο
άρα το τετράπλευρο  είναι εγγράψιμο, και
είναι εγγράψιμο, και  άρα είναι ισοσκελές τραπέζιο.
άρα είναι ισοσκελές τραπέζιο.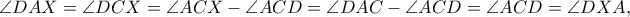
 . Τελικά, λόγω της τριγωνικής ανισότητας,
. Τελικά, λόγω της τριγωνικής ανισότητας,
 ο μέγιστος γνήσιος διαιρέτης του
ο μέγιστος γνήσιος διαιρέτης του  , τότε πρέπει
, τότε πρέπει  , άτοπο αφού
, άτοπο αφού 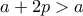 . Άρα
. Άρα  και
και  .
.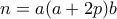 με
με  θετικό ακέραιο. Επίσης,
θετικό ακέραιο. Επίσης,  .
. , τότε
, τότε  , άρα
, άρα  , οπότε
, οπότε 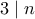 , συνεπώς και
, συνεπώς και  . Αφού όμως
. Αφού όμως  , είναι
, είναι  , συνεπώς
, συνεπώς
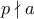 , που δίνει ότι
, που δίνει ότι  , και άρα
, και άρα  , που δίνει το ζητούμενο. Αν τώρα ήταν
, που δίνει το ζητούμενο. Αν τώρα ήταν 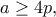 τότε
τότε

 . Έστω τότε
. Έστω τότε 
 , οπότε αφού
, οπότε αφού  , είναι
, είναι  , οπότε είτε
, οπότε είτε  , είτε
, είτε  . Αν ισχύει η πρώτη διαιρετότητα, τότε αφού
. Αν ισχύει η πρώτη διαιρετότητα, τότε αφού 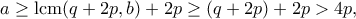

 , τότε
, τότε  άτοπο. Αν
άτοπο. Αν  , τότε
, τότε  άρα
άρα 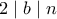 , άτοπο αφού
, άτοπο αφού 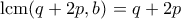 , και άρα
, και άρα  , οπότε
, οπότε 
 δεν είναι πρώτος και είναι
δεν είναι πρώτος και είναι  . Όμοια με πριν, ακολουθούμε την ίδια διαδικασία και προκύπτει άτοπο.
. Όμοια με πριν, ακολουθούμε την ίδια διαδικασία και προκύπτει άτοπο.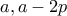 είναι και οι δύο πρώτοι ή
είναι και οι δύο πρώτοι ή  , τότε
, τότε  , με
, με  πρώτο, οπότε
πρώτο, οπότε  γιατί αν
γιατί αν  ο
ο  , άρα
, άρα  , γιατί διαφορετικά πρέπει
, γιατί διαφορετικά πρέπει  , οπότε
, οπότε  άτοπο. Αφού όμως
άτοπο. Αφού όμως  προκύπτει ότι
προκύπτει ότι  , άρα
, άρα που ισοδυναμεί με
που ισοδυναμεί με  , άτοπο.
, άτοπο. , άρα είναι πρώτος.
, άρα είναι πρώτος.  , και αν
, και αν  τότε
τότε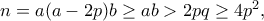
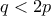 οπότε
οπότε  . Όμως είναι
. Όμως είναι  και άρα
και άρα 
 τότε
τότε  άτοπο, άρα
άτοπο, άρα  .
. τότε
τότε  , οπότε
, οπότε  και άρα
και άρα 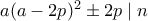 , οπότε σε κάθε περίπτωση
, οπότε σε κάθε περίπτωση , άρα αν
, άρα αν  , τότε
, τότε  , συνεπώς αν
, συνεπώς αν  προκύπτει ότι
προκύπτει ότι
 και
και  , οπότε
, οπότε 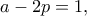 άτοπο.
άτοπο.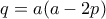 , τότε
, τότε  , οπότε
, οπότε  και άρα
και άρα 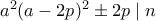 , οπότε σε κάθε περίπτωση
, οπότε σε κάθε περίπτωση , άρα αν
, άρα αν 
 με
με 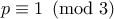 , τότε εύκολα πρέπει
, τότε εύκολα πρέπει  , άρα
, άρα  , οπότε προκύπτει ότι το πλήθος των παράξενους αριθμών είναι μικρότερος από το πλήθος των πρώτων στο
, οπότε προκύπτει ότι το πλήθος των παράξενους αριθμών είναι μικρότερος από το πλήθος των πρώτων στο ![[1,2p] [1,2p]](/forum/ext/geomar/texintegr/latexrender/pictures/79b909591e2d18aa57e731bf71e5670c.png) που είναι
που είναι  . Όμως, σε κάθε έξι διαδοχικούς αριθμούς
. Όμως, σε κάθε έξι διαδοχικούς αριθμούς  ή
ή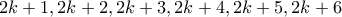 ,
, 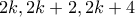 στην πρώτη εξάδα είναι άρτιοι, και οι
στην πρώτη εξάδα είναι άρτιοι, και οι 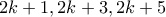 είναι αναδιάταξη των
είναι αναδιάταξη των  . Όμοια στη δεύτερη εξάδα).
. Όμοια στη δεύτερη εξάδα). εξάδες διαδοχικών αριθμών, έχουμε το πολύ
εξάδες διαδοχικών αριθμών, έχουμε το πολύ  παράξενους αριθμούς, όπως θέλαμε.
παράξενους αριθμούς, όπως θέλαμε. των σταθμών ισχύει ότι
των σταθμών ισχύει ότι 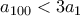 , τότε ποιος είναι ο μέγιστος αριθμός επιτυχημένων σταθμών;"
, τότε ποιος είναι ο μέγιστος αριθμός επιτυχημένων σταθμών;" σταθμά. Έστω
σταθμά. Έστω  τα επιτυχημένα σταθμά. Τότε, ονομάζουμε κάθε σταθμό με βάρος
τα επιτυχημένα σταθμά. Τότε, ονομάζουμε κάθε σταθμό με βάρος 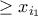 μεγάλο, και μικρό αν έχει βάρος
μεγάλο, και μικρό αν έχει βάρος  . Έχουμε τον ακόλουθο Ισχυρισμό.
. Έχουμε τον ακόλουθο Ισχυρισμό. ένα επιτυχημένο σταθμό και
ένα επιτυχημένο σταθμό και 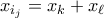 , τότε τα
, τότε τα 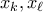 είναι και τα δύο μικρά.
είναι και τα δύο μικρά. ήταν μεγάλο, τότε
ήταν μεγάλο, τότε 
 υπάρχουν
υπάρχουν  με
με  , αφού τα μη διατεταγμένα ζεύγη
, αφού τα μη διατεταγμένα ζεύγη  είναι διαφορετικά για κάθε
είναι διαφορετικά για κάθε  .
.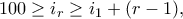 άρα
άρα  , συνεπώς
, συνεπώς
 . Αν
. Αν  , εύκολα προκύπτει ότι πρέπει
, εύκολα προκύπτει ότι πρέπει  , άρα όλα τα σταθμά
, άρα όλα τα σταθμά  είναι επιτυχημένα, και τα υπόλοιπα δεν είναι.
είναι επιτυχημένα, και τα υπόλοιπα δεν είναι.  . Θα επιλέξουμε τα βάρη αυτά ώστε να έχουν τις εξής ιδιότητες:
. Θα επιλέξουμε τα βάρη αυτά ώστε να έχουν τις εξής ιδιότητες:
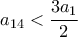 και
και είναι διαφορετικά.
είναι διαφορετικά. , καθώς και ότι
, καθώς και ότι  , ενώ τέλος εξασφαλίζουν ότι μπορούμε να επιλέξουμε από τα
, ενώ τέλος εξασφαλίζουν ότι μπορούμε να επιλέξουμε από τα  διαφορετικά αθροίσματα της μορφής
διαφορετικά αθροίσματα της μορφής  όπως θέλουμε, επιλέγουμε τον
όπως θέλουμε, επιλέγουμε τον  όσο μικρό θέλουμε (αρκεί να είναι
όσο μικρό θέλουμε (αρκεί να είναι  ), με την ιδιότητα τα αθροίσματα
), με την ιδιότητα τα αθροίσματα  με
με  να είναι διαφορετικά από τα ήδη υπάρχοντα αθροίσματα. Είναι σαφές ότι μπορούμε να κάνουμε την επιλογή με αυτόν τον τρόπο.
να είναι διαφορετικά από τα ήδη υπάρχοντα αθροίσματα. Είναι σαφές ότι μπορούμε να κάνουμε την επιλογή με αυτόν τον τρόπο. βάρη (αν έχουμε το πολύ
βάρη (αν έχουμε το πολύ  . Οι κορυφές του χωρίζονται σε δύο υποσύνολα
. Οι κορυφές του χωρίζονται σε δύο υποσύνολα  και
και  κορυφές και το
κορυφές και το  κορυφές ώστε κάθε κορυφή του
κορυφές ώστε κάθε κορυφή του  με τις ίδιες κορυφές ώστε τουλάχιστον
με τις ίδιες κορυφές ώστε τουλάχιστον  κορυφές του να έχουν βαθμό ακριβώς
κορυφές του να έχουν βαθμό ακριβώς  . Αν περιορίσουμε το
. Αν περιορίσουμε το  .
.  με κορυφές τα δέντρα
με κορυφές τα δέντρα  όπου συνδέουμε τα
όπου συνδέουμε τα 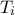 με
με  αν και μόνο αν έχουν δυο γειτονικές κορυφές. Είναι άμεσο ότι το
αν και μόνο αν έχουν δυο γειτονικές κορυφές. Είναι άμεσο ότι το  ακμές. Παρατηρούμε ότι αν έχουμε ακμή μεταξύ των
ακμές. Παρατηρούμε ότι αν έχουμε ακμή μεταξύ των  ακμές μεταξύ κορυφών του
ακμές μεταξύ κορυφών του  δέντρα στο
δέντρα στο 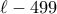 δέντρα στο
δέντρα στο  οπότε
οπότε  . Δηλαδή στο
. Δηλαδή στο  κορυφές βαθμού
κορυφές βαθμού  όπως θέλαμε να δείξουμε.
όπως θέλαμε να δείξουμε. . Από την άλλη κάθε πρόβλημα δίνει συνολικά το πολύ
. Από την άλλη κάθε πρόβλημα δίνει συνολικά το πολύ  βαθμούς σε όσους το έλυσαν. Άρα το άθροισμα των βαθμολογιών είναι το πολύ
βαθμούς σε όσους το έλυσαν. Άρα το άθροισμα των βαθμολογιών είναι το πολύ  . Αυτό όμως είναι άτοπο.
. Αυτό όμως είναι άτοπο.