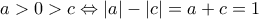12 Μαρτίου 2023
10η τάξη Πρόβλημα 1. Για τους τέσσερεις ακέραιους αριθμούς
είναι γνωστό, ότι ισχύει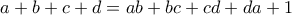 
. Να αποδείξετε, ότι η απόλυτη τιμή κάποιων δυο εξ αυτών διαφέρει κατά
. (Α. Ντολεντένοκ)Πρόβλημα 2. Στην σκυταλοδρομία «Ιερά Οδός» συμμετείχαν δυο ομάδες των
ατόμων. Κάθε ομάδα χώρισε με τον δικό της τρόπο την διαδρομή σε κομμάτια, όχι απαραίτητα ίσα και τα μοίρασε μεταξύ των συμμετεχόντων έτσι, ώστε ο καθένας να τρέξει ακριβώς ένα κομμάτι της διαδρομής (η ταχύτητα κάθε συμμετέχοντα είναι σταθερή, αλλά η ταχύτητα διαφορετικών συμμετεχόντων μπορεί να είναι διαφορετική). Οι πρώτοι συμμετέχοντες κάθε ομάδας ξεκίνησαν ταυτόχρονα και η αλλαγή της σκυτάλης γίνεται στιγμιαία. Ποιος είναι ο μέγιστος αριθμός προσπεράσεων που μπορεί να συμβούν σε ένα τέτοιο αγώνα; Η προήγηση στα άκρα ενός κομματιού διαδρομής δεν θεωρείται προσπέραση. (Ε. Νεουστρόεβα)Πρόβλημα 3. Η περίμετρος του τριγώνου
είναι ίση με . Ο κύκλος 
, εφάπτεται της πλευράς 
, της προέκτασης της πλευράς 
στο σημείο 
και στην προέκταση της πλευράς 
στο σημείο 
. Η ευθεία, που διέρχεται από τα μέσα των και , τέμνει τον περιγεγραμμένο κύκλο του τριγώνου 
στα σημεία 
και 
. Να βρείτε το μήκος του τμήματος 
. (Ντ. Μπρόντσκϊι)Πρόβλημα 4. Στην οθόνη ενός υπερυπολογιστή είναι τυπωμένος ο αριθμός
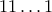(σύνολο 
άσσοι). Κάθε δευτερόλεπτο ο υπερυπολογιστής τον αλλάζει σύμφωνα με τον ακόλουθο κανόνα. Ο αριθμός γράφεται στην μορφή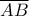 
, όπου ο 
αποτελείται από τα τελευταία δύο ψηφία του και αντικαθίσταται με τον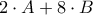 
(αν ο αρχίζει με μηδενικό, τότε αυτό παραλείπεται στον υπολογισμό). Για παράδειγμα, ο αριθμός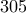 
αντικαθίσταται με τον 
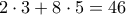. Αν στην οθόνη προκύψει αριθμός μικρότερος του 
, τότε η διαδικασία τερματίζει. Αληθεύει άραγε, ότι η διαδικασία θα τερματίσει; (Μ. Ευδοκίμοβ)Πρόβλημα 5. Στο επίπεδο δίνονται δυο κύκλοι
και 
, που εφάπτονται εξωτερικά. Στον κύκλο διαλέγουμε μια διάμετρο και στον κύκλο μια διάμετρο 
. Θεωρούμε όλες τις δυνατές θέσεις των σημείων 
και 
, για τα οποία το 
είναι κυρτό περιγράψιμο τετράπλευρο και έστω 
το κέντρο του εγγεγραμμένου κύκλου του. Να βρείτε τον γεωμετρικό τόπο των σημείων . (Μ. Ευδοκίμοβ)Πρόβλημα 6. Σε ένα νησί κατοικούν χαμαιλέοντες
χρωμάτων. Όταν ένας χαμαιλέοντας δαγκώνει κάποιον άλλο, το χρώμα αυτού που έχει δαγκωθεί αλλάζει σε ένα από τα χρώματα με κάποιον κανόνα, εξάλλου το καινούργιο χρώμα εξαρτάται μόνο από το χρώμα αυτού που δάγκωσε και από αυτουνού που δαγκώθηκε. Είναι γνωστό, ότι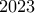 
κόκκινοι χαμαιλέοντες μπορούν να συνεννοηθούν για την ακολουθία των δαγκωμάτων, ώστε ύστερα από αυτή όλοι τους να γίνουν μπλε. Για ποιο ελάχιστο 
μπορούμε να εγγυηθούμε, ότι κόκκινοι χαμαιλέοντες θα μπορέσουν να συνεννοηθούν έτσι, ώστε να γίνουν μπλε; Για παράδειγμα, οι κανόνες μπορεί να είναι ως εξής: αν κόκκινος χαμαιλέοντας δαγκώνει πράσινο, τότε ο χαμαιλέοντας που δαγκώθηκε αλλάζει το χρώμα του σε μπλε- αν πράσινος δαγκώνει κόκκινο, τότε ο χαμαιλέοντας που δαγκώθηκε παραμένει κόκκινος, δηλαδή «αλλάζει το χρώμα του σε κόκκινο» - αν κόκκινος δαγκώνει κόκκινο, τότε αυτός που δαγκώθηκε αλλάζει το χρώμα του σε κίτρινο και ου το κάθε εξής. (Συγκεκριμένοι κανόνες αλλαγής χρωμάτων μπορεί να είναι δομημένοι και διαφορετικά.) (Μ. Ράσκιν)
είναι το κέντρο του 
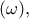τότε η 
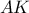είναι διχοτόμος της 
κι επειδή 
ο περίκυκλος του 
Έστω ότι οι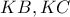 
τον τέμνουν στα 
αντίστοιχα. Έστω ακόμα ότι 
είναι τα μέσα των 
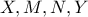είναι συνευθειακά. 
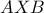η 
είναι διάμεσος και η 
διχοτόμος της εξωτερικής γωνίας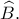 
Αρα οι κόκκινες
Ομοίως βρίσκω 
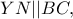οπότε τα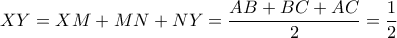 
ή 
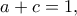τότε επειδή οι αριθμοί είναι ακέραιοι, θα είναι ετερόσημοι ή ένας από τους δύο θα είναι 
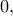το ζητούμενο είναι προφανές. Έστω 