Εκπαιδευτικό κέντρο «Σείριος», Σότσι 21-27 Απριλίου 2023
Θέματα της δεύτερης μέρας για την 11η τάξη.
1. Αρχικά στον πίνακα είναι γραμμένοι
 άσσοι. Η Μαρία και η Ελένη παίζουν ένα παιχνίδι, κάνοντας κινήσεις με την σειρά. Με την δική της κίνηση η Μαρία υψώνει κάποιους
άσσοι. Η Μαρία και η Ελένη παίζουν ένα παιχνίδι, κάνοντας κινήσεις με την σειρά. Με την δική της κίνηση η Μαρία υψώνει κάποιους  αριθμούς του πίνακα στο τετράγωνο. Με την δική της κίνηση η Ελένη διαλέγει μερικούς αριθμούς (πιθανόν, κανένα) του πίνακα και αυξάνει τον καθένα τους κατά
αριθμούς του πίνακα στο τετράγωνο. Με την δική της κίνηση η Ελένη διαλέγει μερικούς αριθμούς (πιθανόν, κανένα) του πίνακα και αυξάνει τον καθένα τους κατά  . Αν κατά την διάρκεια
. Αν κατά την διάρκεια 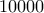 κινήσεων στον πίνακα εμφανιστεί αριθμός, που διαιρείτε με τον
κινήσεων στον πίνακα εμφανιστεί αριθμός, που διαιρείτε με τον 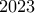 , τότε κερδίζει η Ελένη, αλλιώς κερδίζει η Μαρία. Ποια από τις παίχτριες έχει στρατηγική νίκης, αν πρώτα παίζει η Μαρία; (Γκ. Νικίτιν)
, τότε κερδίζει η Ελένη, αλλιώς κερδίζει η Μαρία. Ποια από τις παίχτριες έχει στρατηγική νίκης, αν πρώτα παίζει η Μαρία; (Γκ. Νικίτιν)2. Το επίπεδο
 τέμνει τις ακμές
τέμνει τις ακμές  ,
,  ,
,  και
και  του τετράεδρου
του τετράεδρου  στα σημεία
στα σημεία  και
και  αντίστοιχα. Προέκυψε, ότι τα σημεία
αντίστοιχα. Προέκυψε, ότι τα σημεία  και
και  βρίσκονται στον κύκλο
βρίσκονται στον κύκλο  , που έχει ως διάμετρο το τμήμα
, που έχει ως διάμετρο το τμήμα  . Το σημείο
. Το σημείο  του επιπέδου
του επιπέδου  είναι τέτοιο, ώστε οι ευθείες
είναι τέτοιο, ώστε οι ευθείες  και
και  να εφάπτονται του κύκλου
να εφάπτονται του κύκλου  . Να αποδείξετε, ότι τα μέσα των ακμών
. Να αποδείξετε, ότι τα μέσα των ακμών  και το σημείο
και το σημείο  είναι συνεπίπεδα. (Α. Κουζνέτσοβ)
είναι συνεπίπεδα. (Α. Κουζνέτσοβ)3. Θα ονομάσουμε ένα πολυώνυμο
 διακέραιο, αν οι αριθμοί
διακέραιο, αν οι αριθμοί 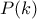 και
και  είναι ακέραιοι για οποιονδήποτε ακέραιο
είναι ακέραιοι για οποιονδήποτε ακέραιο  . Έστω
. Έστω  διακέραιο πολυώνυμο βαθμού
διακέραιο πολυώνυμο βαθμού  και έστω
και έστω  το γινόμενο όλων των σύνθετων αριθμών που δεν υπερβαίνουν το
το γινόμενο όλων των σύνθετων αριθμών που δεν υπερβαίνουν το  (το γινόμενο κενού συνόλου παραγόντων θεωρούμε ότι είναι ίσο με
(το γινόμενο κενού συνόλου παραγόντων θεωρούμε ότι είναι ίσο με  ). Να αποδείξετε ότι ο μεγιστοβάθμιος συντελεστής του πολυώνυμου
). Να αποδείξετε ότι ο μεγιστοβάθμιος συντελεστής του πολυώνυμου  είναι ακέραιος. (Ι. Μπογκντάνοβ, Γκ. Τσελνόκοβ)
είναι ακέραιος. (Ι. Μπογκντάνοβ, Γκ. Τσελνόκοβ)4. Σε μια χώρα υπάρχουν
 πόλεις. Σε αυτήν λειτουργούν
πόλεις. Σε αυτήν λειτουργούν  μονόδρομοι (κατεύθυνση προς μια πλευρά): από ένας δρόμος από την πόλη
μονόδρομοι (κατεύθυνση προς μια πλευρά): από ένας δρόμος από την πόλη  στην
στην  για κάθε διατεταγμένο ζεύγος πόλεων
για κάθε διατεταγμένο ζεύγος πόλεων  . Κάθε δρόμος έχει το κόστος λειτουργίας του. Για ένα δοθέν
. Κάθε δρόμος έχει το κόστος λειτουργίας του. Για ένα δοθέν  εξετάζουμε όλους τους τρόπους επιλογής
εξετάζουμε όλους τους τρόπους επιλογής  πόλεων και
πόλεων και  δρόμων έτσι, ώστε από κάθε πόλη να μπορούμε να μεταβούμε σε κάποια επιλεχθείσα πόλη, χρησιμοποιώντας μόνο τους επιλεχθέντες δρόμους. Ένα τέτοιο σύστημα πόλεων και δρόμων με το ελάχιστο άθροισμα κόστους λειτουργίας θα το ονομάσουμε
δρόμων έτσι, ώστε από κάθε πόλη να μπορούμε να μεταβούμε σε κάποια επιλεχθείσα πόλη, χρησιμοποιώντας μόνο τους επιλεχθέντες δρόμους. Ένα τέτοιο σύστημα πόλεων και δρόμων με το ελάχιστο άθροισμα κόστους λειτουργίας θα το ονομάσουμε  βέλτιστο. Να αποδείξετε, ότι τις πόλεις μπορούμε να τις αριθμήσουμε από το
βέλτιστο. Να αποδείξετε, ότι τις πόλεις μπορούμε να τις αριθμήσουμε από το  έως το
έως το  έτσι, ώστε για κάθε
έτσι, ώστε για κάθε  να υπάρχει
να υπάρχει  βέλτιστο σύστημα δρόμων με επιλεχθείσες πόλεις
βέλτιστο σύστημα δρόμων με επιλεχθείσες πόλεις  . (Β. Μπούσλοβ)
. (Β. Μπούσλοβ)
 . Αυτό είναι αρκετό, επειδή
. Αυτό είναι αρκετό, επειδή  . Η στρατηγική της Μαρίας είναι απλώς να επιλέγει εναλλάξ τους
. Η στρατηγική της Μαρίας είναι απλώς να επιλέγει εναλλάξ τους  , τότε αυτό σημαίνει ότι ακριβώς πριν κινηθεί η Ελένη υπήρχε ο αριθμός
, τότε αυτό σημαίνει ότι ακριβώς πριν κινηθεί η Ελένη υπήρχε ο αριθμός  στον πίνακα. Διακρίνουμε δύο περιπτώσεις:
στον πίνακα. Διακρίνουμε δύο περιπτώσεις: ανήκει στους πρώτους
ανήκει στους πρώτους  ή
ή  , που είναι άτοπο.
, που είναι άτοπο. ή
ή  , που είναι άτοπο.
, που είναι άτοπο.