ΘΕΜΑ ΣΤΕΡΕΟΜΕΤΡΙΑΣ ΣΕ ΓΕΡΜΑΝΙΚΟ ΔΙΑΓΩΝΙΣΜΟ
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1292
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
ΘΕΜΑ ΣΤΕΡΕΟΜΕΤΡΙΑΣ ΣΕ ΓΕΡΜΑΝΙΚΟ ΔΙΑΓΩΝΙΣΜΟ
Το θέμα που προτείνω τέθηκε στον 20ο Γερμανικό Ομοσπονδιακό Μαθηματικό Διαγωνισμό του 1989-1990 στον πρώτο γύρο.
Αναδεικνύει ένα χαρακτηριστικό σημείο του τετραέδρου.
Έστω ότι δύο οποιεσδήποτε απέναντι ακμές ενός τετραέδρου είναι ορθογώνιες.
Δείξτε ότι τα μέσα των έξη ακμών βρίσκονται πάνω σε σφαίρα.
Αναδεικνύει ένα χαρακτηριστικό σημείο του τετραέδρου.
Έστω ότι δύο οποιεσδήποτε απέναντι ακμές ενός τετραέδρου είναι ορθογώνιες.
Δείξτε ότι τα μέσα των έξη ακμών βρίσκονται πάνω σε σφαίρα.
Λέξεις Κλειδιά:
- Al.Koutsouridis
- Δημοσιεύσεις: 1810
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: ΘΕΜΑ ΣΤΕΡΕΟΜΕΤΡΙΑΣ ΣΕ ΓΕΡΜΑΝΙΚΟ ΔΙΑΓΩΝΙΣΜΟ
ΈστωΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Δευ Φεβ 19, 2024 9:12 pmΤο θέμα που προτείνω τέθηκε στον 20ο Γερμανικό Ομοσπονδιακό Μαθηματικό Διαγωνισμό του 1989-1990 στον πρώτο γύρο.
Αναδεικνύει ένα χαρακτηριστικό σημείο του τετραέδρου.
Έστω ότι δύο οποιεσδήποτε απέναντι ακμές ενός τετραέδρου είναι ορθογώνιες.
Δείξτε ότι τα μέσα των έξη ακμών βρίσκονται πάνω σε σφαίρα.
 ένα τετράεδρο και έστω
ένα τετράεδρο και έστω 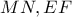 και
και  τα ευθύγραμμα τμήματα, που ενώνουν τα μέσα των ζευγών απέναντι ακμών
τα ευθύγραμμα τμήματα, που ενώνουν τα μέσα των ζευγών απέναντι ακμών  και
και  ,
,  και
και  ,
,  και
και 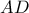 αντίστοιχα.
αντίστοιχα. Εφόσον
 ,
, 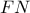 είναι παράλληλα προς την ακμή
είναι παράλληλα προς την ακμή  και ίσα με το μισό της, τότε το τετράπλευρο
και ίσα με το μισό της, τότε το τετράπλευρο 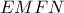 είναι παραλληλόγραμμο και το σημείο τομής των διαγωνίων του
είναι παραλληλόγραμμο και το σημείο τομής των διαγωνίων του  διχοτομεί τις διαγωνίους
διχοτομεί τις διαγωνίους  ,
, 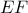 . Ομοίως από το παραλληλόγραμμο
. Ομοίως από το παραλληλόγραμμο 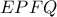 προκύπτει ότι το
προκύπτει ότι το  είναι μέσο και των
είναι μέσο και των  ,
,  . Δηλαδή τα ευθύγραμμα τμήματα
. Δηλαδή τα ευθύγραμμα τμήματα 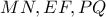 συντρέχουν και διχοτομούνται από το σημείο
συντρέχουν και διχοτομούνται από το σημείο  .
.Υπολογίζουμε το μήκος του τμήματος
 . Έχουμε
. Έχουμε 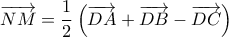 , οπότε θα είναι
, οπότε θα είναι 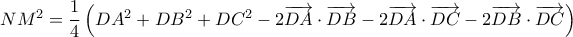
Όμως από τον νόμο συνημιτόνων ισχύουν οι ισότητες
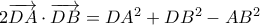 (α1)
(α1)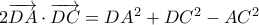 (α2)
(α2)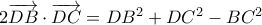 (α3)
(α3)Οπότε θα έχουμε
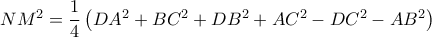 (β1)
(β1)και ανάλογα για τα τμήματα
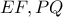
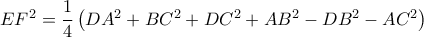 (β2)
(β2)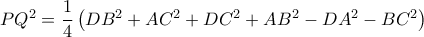 (β3)
(β3)Από την καθετότητα των απέναντι ακμών έχουμε
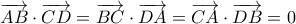
και εφόσον
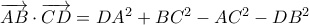 (αφαίρεση κατά μέλη των (α2), (α3)) , προκύπτουν οι ισότητες
(αφαίρεση κατά μέλη των (α2), (α3)) , προκύπτουν οι ισότητες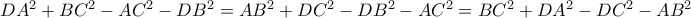 (γ1)
(γ1)ή ισοδύναμα
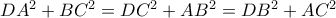 (γ2)
(γ2)Αντικαθιστώντας τις (γ1) ή (γ2) στις εκφράσεις για τα
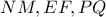 βρίσκουμε, ότι
βρίσκουμε, ότι 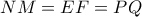 .
.Άρα εφόσον το σημείο
 διχοτομεί τα παραπάνω τμήματα και αυτά είναι ίσα μεταξύ τους, το
διχοτομεί τα παραπάνω τμήματα και αυτά είναι ίσα μεταξύ τους, το  θα ισαπέχει από τα σημεία
θα ισαπέχει από τα σημεία 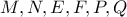 , που αποδεικνύει το ζητούμενο.
, που αποδεικνύει το ζητούμενο.-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1292
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
Re: ΘΕΜΑ ΣΤΕΡΕΟΜΕΤΡΙΑΣ ΣΕ ΓΕΡΜΑΝΙΚΟ ΔΙΑΓΩΝΙΣΜΟ
Nα ευχαριστήσω τον Αλέξανδρο Κουτσουρίδη για τη λύση του.
Επίσης πρέπει να τον ευχαριστήσω γιατί με προσωπικό μήνυμα μου επισήμανε την παράλειψη της λέξης '' απέναντι '' στη διατύπωση
του θέματος, ήμουν απρόσεκτος...
Θέλω να γράψω τις δικές μου σκέψεις για το θέμα.
Αυτό το σημείο που ο Αλέξανδρος ονόμασε αποτελεί ένα χαρακτηριστικό σημείο του τετραέδρου, το βαρύκεντρο.
αποτελεί ένα χαρακτηριστικό σημείο του τετραέδρου, το βαρύκεντρο.
Σε παλαιότερα σχολικά βιβλία, όπως του Χρήστου Παπανικολάου ή των Βαρουχάκη-Παπαμιχαήλ-Αλιμπινίση-Κοντογιάννη, το σημείο
αυτό αναφέρεται στη θεωρία. Θα παραθέσω αμέσως τα όσα θεωρώ δεδομένα από τη θεωρία.
Διάμεσος τετραέδρου λέγεται το τμήμα με άκρα μια κορυφή και το βαρύκεντρο της απέναντι έδρας του τετραέδρου.
Αποδεικνύεται ότι:
Σε κάθε τετράεδρο οι τέσσερεις διάμεσοι διέρχονται από το ίδιο σημείο.
Το σημείο αυτό λέγεται βαρύκεντρο και απέχει από κάθε κορυφή απόσταση ίση
με τα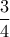 της αντίστοιχης διαμέσου.
της αντίστοιχης διαμέσου.
Αποδεικνύεται επίσης ότι αν είναι το βαρύκεντρο τετραέδρου
είναι το βαρύκεντρο τετραέδρου  τότε
τότε
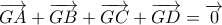
Aυτά τα θεώρησα δεδομένα όταν αποπειράθηκα να λύσω το θέμα.
Έστω το μέσο της ακμής
το μέσο της ακμής 
Έστω το μέσο της ακμής
το μέσο της ακμής 
Έστω το μέσο της ακμής
το μέσο της ακμής 
Έστω το μέσο της ακμής
το μέσο της ακμής 
Έστω το μέσο της ακμής
το μέσο της ακμής 
Έστω το μέσο της ακμής
το μέσο της ακμής 
Ισχύει ότι
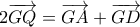
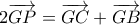
Συνεπώς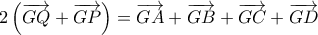 και έτσι
και έτσι
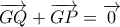
Mε αντίστοιχες σκέψεις προκύπτει ότι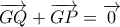
Έτσι το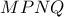 είναι παραλληλόγραμμο με κέντρο συμμετρίας το
είναι παραλληλόγραμμο με κέντρο συμμετρίας το 
Από το τρίγωνο προκύπτει ότι
προκύπτει ότι  παράλληλη της
παράλληλη της 
Από το τρίγωνο προκύπτει ότι
προκύπτει ότι  παράλληλη της
παράλληλη της 
Άρα το παραλληλόγραμμο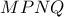 είναι ορθογώνιο.
είναι ορθογώνιο.
Άρα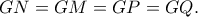
Δεν υπάρχει λόγος να σας κουράζω, με αντίστοιχες σκέψεις προκύπτει ότι το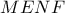 είναι παραλληλόγραμμο
είναι παραλληλόγραμμο
με κέντρο συμμετρίας το και μάλιστα ορθογώνιο.
και μάλιστα ορθογώνιο.
Άρα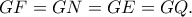
Άρα τα σημεία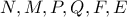 βρίσκονται πάνω στην επιφάνεια σφαίρας κέντρου
βρίσκονται πάνω στην επιφάνεια σφαίρας κέντρου 
Επίσης πρέπει να τον ευχαριστήσω γιατί με προσωπικό μήνυμα μου επισήμανε την παράλειψη της λέξης '' απέναντι '' στη διατύπωση
του θέματος, ήμουν απρόσεκτος...
Θέλω να γράψω τις δικές μου σκέψεις για το θέμα.
Αυτό το σημείο που ο Αλέξανδρος ονόμασε
 αποτελεί ένα χαρακτηριστικό σημείο του τετραέδρου, το βαρύκεντρο.
αποτελεί ένα χαρακτηριστικό σημείο του τετραέδρου, το βαρύκεντρο.Σε παλαιότερα σχολικά βιβλία, όπως του Χρήστου Παπανικολάου ή των Βαρουχάκη-Παπαμιχαήλ-Αλιμπινίση-Κοντογιάννη, το σημείο
αυτό αναφέρεται στη θεωρία. Θα παραθέσω αμέσως τα όσα θεωρώ δεδομένα από τη θεωρία.
Διάμεσος τετραέδρου λέγεται το τμήμα με άκρα μια κορυφή και το βαρύκεντρο της απέναντι έδρας του τετραέδρου.
Αποδεικνύεται ότι:
Σε κάθε τετράεδρο οι τέσσερεις διάμεσοι διέρχονται από το ίδιο σημείο.
Το σημείο αυτό λέγεται βαρύκεντρο και απέχει από κάθε κορυφή απόσταση ίση
με τα
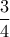 της αντίστοιχης διαμέσου.
της αντίστοιχης διαμέσου.Αποδεικνύεται επίσης ότι αν
 είναι το βαρύκεντρο τετραέδρου
είναι το βαρύκεντρο τετραέδρου  τότε
τότε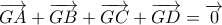
Aυτά τα θεώρησα δεδομένα όταν αποπειράθηκα να λύσω το θέμα.
Έστω
 το μέσο της ακμής
το μέσο της ακμής 
Έστω
 το μέσο της ακμής
το μέσο της ακμής 
Έστω
 το μέσο της ακμής
το μέσο της ακμής 
Έστω
 το μέσο της ακμής
το μέσο της ακμής 
Έστω
 το μέσο της ακμής
το μέσο της ακμής 
Έστω
 το μέσο της ακμής
το μέσο της ακμής 
Ισχύει ότι
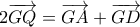
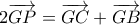
Συνεπώς
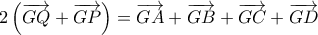 και έτσι
και έτσι 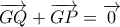
Mε αντίστοιχες σκέψεις προκύπτει ότι
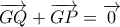
Έτσι το
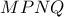 είναι παραλληλόγραμμο με κέντρο συμμετρίας το
είναι παραλληλόγραμμο με κέντρο συμμετρίας το 
Από το τρίγωνο
 προκύπτει ότι
προκύπτει ότι  παράλληλη της
παράλληλη της 
Από το τρίγωνο
 προκύπτει ότι
προκύπτει ότι  παράλληλη της
παράλληλη της 
Άρα το παραλληλόγραμμο
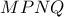 είναι ορθογώνιο.
είναι ορθογώνιο.Άρα
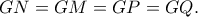
Δεν υπάρχει λόγος να σας κουράζω, με αντίστοιχες σκέψεις προκύπτει ότι το
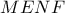 είναι παραλληλόγραμμο
είναι παραλληλόγραμμομε κέντρο συμμετρίας το
 και μάλιστα ορθογώνιο.
και μάλιστα ορθογώνιο.Άρα
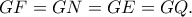
Άρα τα σημεία
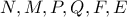 βρίσκονται πάνω στην επιφάνεια σφαίρας κέντρου
βρίσκονται πάνω στην επιφάνεια σφαίρας κέντρου 
- Al.Koutsouridis
- Δημοσιεύσεις: 1810
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: ΘΕΜΑ ΣΤΕΡΕΟΜΕΤΡΙΑΣ ΣΕ ΓΕΡΜΑΝΙΚΟ ΔΙΑΓΩΝΙΣΜΟ
Όπως είδαμε π.χ. εδώ το εν λόγω τετράεδρο είναι ορθοκεντρικό.ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Δευ Φεβ 19, 2024 9:12 pm
Έστω ότι δύο οποιεσδήποτε απέναντι ακμές ενός τετραέδρου είναι ορθογώνιες.
Δείξτε ότι τα μέσα των έξη ακμών βρίσκονται πάνω σε σφαίρα.
Η υπό εξέταση σφαίρα είναι μια από τις χαρακτηριστηκές σφαίρες σε ένα ορθοκεντρικό τετράεδρο. Η σφαίρα αυτή ονομάζεται συχνά σφαίρα των 24 σημείων ή πρώτη σφαίρα του Euler. Καθώς πέρα των παρπάνω έξη σημειών, άλλα έξη σημεία, οι βάσεις των κοινών κάθετων τμημάτων απέναντι ακμών καθώς και 12 σημεία, τα μέσα των τμημάτων που ορίζουν το ορθόκεντρο και οι κορυφές κάθε έδρας, ανήκουν σε αυτή την σφαίρα.
- S.E.Louridas
- Δημοσιεύσεις: 5959
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: ΘΕΜΑ ΣΤΕΡΕΟΜΕΤΡΙΑΣ ΣΕ ΓΕΡΜΑΝΙΚΟ ΔΙΑΓΩΝΙΣΜΟ
Μετά από τις καταπληκτικές λύσεις που προηγήθηκαν, ας δούμε και την άποψη που ακολουθεί:ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Δευ Φεβ 19, 2024 9:12 pmΈστω ότι δύο οποιεσδήποτε απέναντι ακμές ενός τετραέδρου είναι ορθογώνιες.
Δείξτε ότι τα μέσα των έξη ακμών βρίσκονται πάνω σε σφαίρα.
Αν υποθέσουμε ότι
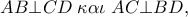 τότε «αυτόματα» παίρνουμε και
τότε «αυτόματα» παίρνουμε και 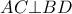 (Θεώρημα γνωστό με απλή απόδειξη). Έτσι τα τετράπλευρα
(Θεώρημα γνωστό με απλή απόδειξη). Έτσι τα τετράπλευρα 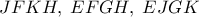 προκύπτουν ορθογώνια αφού
προκύπτουν ορθογώνια αφού 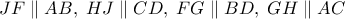 και με βάση τις διδόμενες καθετότητες. Αυτό σημαίνει ότι όλες οι διαγώνιες τους συντρέχουν σε σημείο
και με βάση τις διδόμενες καθετότητες. Αυτό σημαίνει ότι όλες οι διαγώνιες τους συντρέχουν σε σημείο  και είναι και ίσες. Άρα υπάρχει σφαίρα κέντρου
και είναι και ίσες. Άρα υπάρχει σφαίρα κέντρου  που περνά από τα μέσα των έξι πλευρών του στερεού μας.
που περνά από τα μέσα των έξι πλευρών του στερεού μας. S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες
