Μαθηματική Ολυμπιάδα Μόσχας 2024 (7η τάξη)

[Al.Koutsouridis]

LXXXVIΙ Μαθηματική Ολυμπιάδα Μόσχας
XXXV Μαθηματική Γιορτή - 18 Φεβρουαρίου 2024 7η τάξη

Πρόβλημα 1. Τοποθετήστε στα κελιά ενός πίνακα διαφορετικούς θετικούς ακέραιους αριθμούς, όχι μεγαλύτερους του , έτσι, ώστε σε οποιοδήποτε ζεύγος γειτονικών κατά πλευρά κελιών ο ένας αριθμός να διαιρείται με τον άλλον. [4 μόρια] (Ι. Ιάσενκο)

Πρόβλημα 2. Ο Κωνσταντίνος επισκέφτηκε ένα μουσείο σύγχρονης τέχνης και είδε έναν τετράγωνο πίνακα σε κορνίζα παράξενης μορφής, που αποτελείται από ίσα τρίγωνα. Ο Κωνσταντίνος αναρωτήθηκε, με τι ισούνται οι γωνίες αυτών των τριγώνων. Βοηθήστε τον να τις βρει. [5 μόρια] (Ι. Ρούσκιχ)

Screenshot 2024-03-01 at 17.57.46.png (28.91 KiB) Προβλήθηκε 204 φορές

Πρόβλημα 3. Στο άθροισμα



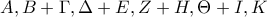
(σημ. μετ. στο πρωτότυπο υπάρχει το άθροισμα П,Я + Т,Ь + Д,Р + О,Б + Е,Й που διαβάζεται ως "πέντε κλάσματα") όλα τα ψηφία είναι κωδικοποιημένα με γράμματα (με διαφορετικά γράμματα διαφορετικά ψηφία). Προέκυψε, ότι κανένας εκ των πέντε προσθετέων δεν είναι ακέραιος, ενώ το άθροισμα είναι ακέραιος. Ποιο ακριβώς; Για κάθε πιθανή απάντηση γράψτε ένα παράδειγμα με πέντε τέτοιους προσθετέους. Εξηγήστε γιατί δεν μπορούν προκύψουν άλλα αθροίσματα. [7 μόρια] (Α. Σαποβάλοβ)

Πρόβλημα 4. O Γιώργος σχημάτισε με οχτώ τουβλάκια ένα κύβο (βλ. σχήμα). Όλα τα τουβλάκια έχουν τον ίδιο όγκο, τα γκρι τουβλάκια είναι ίδια μεταξύ τους και τα λευκά επίσης ίδια μεταξύ τους. Ποιο μέρος της ακμής του κύβου αποτελεί το μήκος, το πλάτος και το ύψος του άσπρου τούβλου; [7 μόρια] (Μ. Ευδοκίμοβ)

Screenshot 2024-03-01 at 17.58.07.png (9.72 KiB) Προβλήθηκε 204 φορές

Πρόβλημα 5. Σε ένα νησί κατοικούν κόκκινοι, μπλε και πράσινοι χαμαιλέοντες. 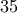χαμαιλέοντες στάθηκαν σε ένα κύκλο. Ύστερα από ένα λεπτό όλοι τους ταυτόχρονα άλλαξαν χρώμα, ο καθένας τους στο χρώμα ενός εκ των γειτόνων του. Ύστερα από επιπλέον ένα λεπτό εκ νέου όλοι τους ταυτόχρονα άλλαξαν χρώμα, στο χρώμα ενός εκ των γειτόνων τους. Μπορεί άραγε να προέκυψε, ότι κάθε χαμαιλέοντας υπήρξε και κόκκινος και μπλε και πράσινος; [9 μόρια] (Ι. Ρούσκιχ)

Πρόβλημα 6. Διαμερίστε το πρώτο παραλληλόγραμμο σε τρία κομμάτια και σχηματίστε από αυτά το δεύτερο παραλληλόγραμμο. Στην απάντηση σχεδιάστε, πως θα είναι διαμερισμένα και τα δυο παραλληλόγραμμα. [9 μόρια] (Τ. Γκολενίστσεβα-Κουτούζοβα)

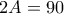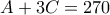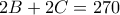Screenshot 2024-03-01 at 17.58.23.png (9.32 KiB) Προβλήθηκε 204 φορές

[Mihalis_Lambrou]

Πρόβλημα 1. Τοποθετήστε στα κελιά ενός πίνακα διαφορετικούς θετικούς ακέραιους αριθμούς, όχι μεγαλύτερους του , έτσι, ώστε σε οποιοδήποτε ζεύγος γειτονικών κατά πλευρά κελιών ο ένας αριθμός να διαιρείται με τον άλλον. [4 μόρια] (Ι. Ιάσενκο)

.

[Mihalis_Lambrou]

Πρόβλημα 2. Ο Κωνσταντίνος επισκέφτηκε ένα μουσείο σύγχρονης τέχνης και είδε έναν τετράγωνο πίνακα σε κορνίζα παράξενης μορφής, που αποτελείται από ίσα τρίγωνα. Ο Κωνσταντίνος αναρωτήθηκε, με τι ισούνται οι γωνίες αυτών των τριγώνων. Βοηθήστε τον να τις βρει. [5 μόρια] (Ι. Ρούσκιχ)

Από την πάνω αριστερή κορυφή του τετραγώνου, κοιτώντας το εξωτερικό της γωνίας του, έχουμε .

Από την κάτω αριστερή κορυφή του τετραγώνου, κοιτώντας το εξωτερικό της γωνίας του, έχουμε .

Από την πάνω δεξιά κορυφή του τετραγώνου, κοιτώντας το εξωτερικό της γωνίας του, έχουμε .

Λύνοντας το σύστημα είναι .