Θέματα των τάξεων 8η και 9η για το έτος 2004.
1. Δίνεται ένα δευτεροβάθμιο τριώνυμο
 με διαφορετικές θετικές ρίζες. Προέκυψε, ότι μεταξύ των ριζών του πολυώνυμου
με διαφορετικές θετικές ρίζες. Προέκυψε, ότι μεταξύ των ριζών του πολυώνυμου  υπάρχουν δυο αρνητικές. Να αποδείξετε, ότι οι ρίζες του
υπάρχουν δυο αρνητικές. Να αποδείξετε, ότι οι ρίζες του  είναι μικρότερες του
είναι μικρότερες του  . (Σ. Μπέρλοβ)
. (Σ. Μπέρλοβ)2. Το
 είναι κυρτό τετράπλευρο, στο οποίο
είναι κυρτό τετράπλευρο, στο οποίο 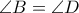 και το κέντρο του περιγεγραμμένου κύκλου του τριγώνου
και το κέντρο του περιγεγραμμένου κύκλου του τριγώνου  , το ορθόκεντρο
, το ορθόκεντρο  του τριγώνου
του τριγώνου  και το σημείο
και το σημείο  είναι συνευθειακά. Να αποδείξετε ότι το
είναι συνευθειακά. Να αποδείξετε ότι το  είναι παραλληλόγραμμο. (Σ. Μπέρλοβ)
είναι παραλληλόγραμμο. (Σ. Μπέρλοβ)3. Σε ένα πίνακα
 είναι τοποθετημένα μερικά πιόνια έτσι, ώστε για κάθε πιόνι όλα τα κελιά, που βρίσκονται δεξιά ή κάτω από αυτό, επίσης είναι κατειλημμένα με πιόνια. Έστω ότι στην
είναι τοποθετημένα μερικά πιόνια έτσι, ώστε για κάθε πιόνι όλα τα κελιά, που βρίσκονται δεξιά ή κάτω από αυτό, επίσης είναι κατειλημμένα με πιόνια. Έστω ότι στην  οστή γραμμή από πάνω υπάρχουν
οστή γραμμή από πάνω υπάρχουν  πιόνια και στην
πιόνια και στην  οστή στήλη από αριστερά
οστή στήλη από αριστερά 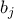 πιόνια. Να αποδείξετε, ότι οι συλλογές των αριθμών
πιόνια. Να αποδείξετε, ότι οι συλλογές των αριθμών  και
και 
συμπίπτουν. (Κ. Κόχας)
4. Το γινόμενο των μη μηδενικών φυσικών αριθμών
 και
και  , είναι κύβος του φυσικού αριθμού
, είναι κύβος του φυσικού αριθμού  , με
, με 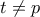 . Να αποδείξετε, ότι
. Να αποδείξετε, ότι ![\left| p^2-q\right| > \dfrac{t^2}{\sqrt[3]{q}} \left| p^2-q\right| > \dfrac{t^2}{\sqrt[3]{q}}](/forum/ext/geomar/texintegr/latexrender/pictures/1127f7dbebdd5469a59ba737661f5386.png) .
. (Σ. Μπέρλοβ)
5. Σε ένα γράφο
 για οποιοδήποτε σύνολο κορυφών του το πλήθος των κορυφών σε αυτό το σύνολο δεν υπερβαίνει το πλήθος των κορυφών, γειτονικών (που συνδέονται με ακμή) τουλάχιστον με μια κορυφή από αυτό το σύνολο. Να αποδείξετε ότι σε αυτόν τον γράφο μπορούμε να πετάξουμε το πολύ το ένα τρίτο των κορυφών με τέτοιο τρόπο, ώστε οι υπόλοιπες κορυφές να μπορούν να διαμεριστούν σε μη τεμνόμενα ζεύγη γειτονικών κορυφών. (Σ. Μπέρλοβ)
για οποιοδήποτε σύνολο κορυφών του το πλήθος των κορυφών σε αυτό το σύνολο δεν υπερβαίνει το πλήθος των κορυφών, γειτονικών (που συνδέονται με ακμή) τουλάχιστον με μια κορυφή από αυτό το σύνολο. Να αποδείξετε ότι σε αυτόν τον γράφο μπορούμε να πετάξουμε το πολύ το ένα τρίτο των κορυφών με τέτοιο τρόπο, ώστε οι υπόλοιπες κορυφές να μπορούν να διαμεριστούν σε μη τεμνόμενα ζεύγη γειτονικών κορυφών. (Σ. Μπέρλοβ)6. Στις πλευρές
 και
και  ενός κυρτού τετράπλευρου
ενός κυρτού τετράπλευρου  δίνονται τα σημεία
δίνονται τα σημεία  και
και  αντίστοιχα, εξάλλου προέκυψε ότι
αντίστοιχα, εξάλλου προέκυψε ότι 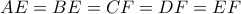 . Οι διαγώνιοι των τετράπλευρων
. Οι διαγώνιοι των τετράπλευρων  και
και  τέμνονται στα σημεία
τέμνονται στα σημεία  και
και  αντίστοιχα. Οι κάθετες από τα σημεία
αντίστοιχα. Οι κάθετες από τα σημεία  και
και  προς τις πλευρές
προς τις πλευρές  και
και  αντίστοιχα τέμνονται στο σημείο
αντίστοιχα τέμνονται στο σημείο  . Να αποδείξετε ότι
. Να αποδείξετε ότι 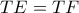 . (Α. Σμιρνόβ)
. (Α. Σμιρνόβ)7. Δίνεται ένας περιττός πρώτος αριθμός
 . Εξετάζουμε το σύνολο
. Εξετάζουμε το σύνολο 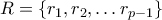 όλων των φυσικών αριθμών (μη μηδενικών), μικρότερων του
όλων των φυσικών αριθμών (μη μηδενικών), μικρότερων του  . Με
. Με  συμβολίζουμε το πλήθος των μη κενών υποσυνόλων
συμβολίζουμε το πλήθος των μη κενών υποσυνόλων  του συνόλου
του συνόλου 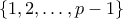 , για τα οποία το άθροισμα
, για τα οποία το άθροισμα 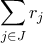 αφήνει υπόλοιπο
αφήνει υπόλοιπο  στην διαίρεση με το
στην διαίρεση με το  . Να αποδείξετε ότι
. Να αποδείξετε ότι  . (Π. Κοζέβνικοβ)
. (Π. Κοζέβνικοβ)8. Να αποδείξετε ότι για τους θετικούς αριθμούς
 ισχύει η ανισότητα
ισχύει η ανισότητα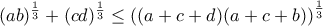 .
. (Φ. Πετρόβ)

 και
και  το γινόμενο τους είναι κύβος του 2 ωστόσο
το γινόμενο τους είναι κύβος του 2 ωστόσο 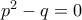
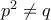 . Θα το μελέτήσω παραπέρα και θα επανέρθω αν είναι.
. Θα το μελέτήσω παραπέρα και θα επανέρθω αν είναι.