Θέματα της πρώτης μέρας για την 9η τάξη.
1. Ο Κώστας και ο Νίκος ξέρουν μόνο τους φυσικούς αριθμούς, που δεν υπερβαίνουν το
 . Ο Κώστας θεωρεί καλούς τους αριθμούς που μπορούν να γραφούν στην μορφή
. Ο Κώστας θεωρεί καλούς τους αριθμούς που μπορούν να γραφούν στην μορφή  , όπου
, όπου  και
και  φυσικοί αριθμοί, όχι μικρότεροι του
φυσικοί αριθμοί, όχι μικρότεροι του  . Ο Νίκος θεωρεί καλούς τους αριθμούς, που μπορούν να γραφούν στην μορφή
. Ο Νίκος θεωρεί καλούς τους αριθμούς, που μπορούν να γραφούν στην μορφή  , όπου
, όπου  και
και  φυσικοί αριθμοί, μεγαλύτεροι του
φυσικοί αριθμοί, μεγαλύτεροι του  . Για ποιόν από τους δυο οι καλοί αριθμοί είναι περισσότεροι; (Ι. Μπογκντάνοβ)
. Για ποιόν από τους δυο οι καλοί αριθμοί είναι περισσότεροι; (Ι. Μπογκντάνοβ)2. Ένας φυσικός αριθμός έχει ακριβώς
 διαιρέτες. Μπορεί άραγε να προκύψει έτσι, ώστε καμία διαφορά δυο διαφορετικών διαιρετών του να μην διαιρείτε με το
διαιρέτες. Μπορεί άραγε να προκύψει έτσι, ώστε καμία διαφορά δυο διαφορετικών διαιρετών του να μην διαιρείτε με το  ; (Επιτροπή διαγωνισμού στο μοτίβο προβλήματος του Α. Τσιρόνοβ)
; (Επιτροπή διαγωνισμού στο μοτίβο προβλήματος του Α. Τσιρόνοβ)3. Σε δυο παιδιά δόθηκε από ένα σακί πατάτες, σε κάθε σακί από
 κονδύλους. Τα παιδιά με την σειρά μεταφέρουν πατάτες, ο καθένας με την επόμενη κίνησή του μεταφέρει μη μηδενικό πλήθος κονδύλων από το σακί του στο σακί του άλλου. Εξάλλου πρέπει να τηρούν την συνθήκη νέας ευκαιρίας: σε κάθε κίνηση το παιδί πρέπει να μεταφέρει περισσότερους κονδύλους, από ότι είχε στο σακί κατά την οποιαδήποτε προηγούμενη κίνησή του (αν υπήρχαν τέτοιες κινήσεις). Έτσι, ως πρώτη κίνηση ένα παιδί μπορεί μεταφέρει οποιοδήποτε μη μηδενικό αριθμό κονδύλων, αλλά ως πέμπτη κίνηση μπορεί να μεταφέρει
κονδύλους. Τα παιδιά με την σειρά μεταφέρουν πατάτες, ο καθένας με την επόμενη κίνησή του μεταφέρει μη μηδενικό πλήθος κονδύλων από το σακί του στο σακί του άλλου. Εξάλλου πρέπει να τηρούν την συνθήκη νέας ευκαιρίας: σε κάθε κίνηση το παιδί πρέπει να μεταφέρει περισσότερους κονδύλους, από ότι είχε στο σακί κατά την οποιαδήποτε προηγούμενη κίνησή του (αν υπήρχαν τέτοιες κινήσεις). Έτσι, ως πρώτη κίνηση ένα παιδί μπορεί μεταφέρει οποιοδήποτε μη μηδενικό αριθμό κονδύλων, αλλά ως πέμπτη κίνηση μπορεί να μεταφέρει  , αν πριν την πρώτη, δεύτερη, τρίτη και τέταρτη κίνησή του ο αριθμός των κονδύλων στο σακί του ήταν μικρότερος του
, αν πριν την πρώτη, δεύτερη, τρίτη και τέταρτη κίνησή του ο αριθμός των κονδύλων στο σακί του ήταν μικρότερος του  . Ποιος είναι ο μέγιστος συνολικά αριθμός κινήσεων που μπορούν να κάνουν τα παιδιά; (Ε. Μολτσάνοβ)
. Ποιος είναι ο μέγιστος συνολικά αριθμός κινήσεων που μπορούν να κάνουν τα παιδιά; (Ε. Μολτσάνοβ)4. Δίνεται ένα εγγεγραμμένο τετράπλευρο
 , στο οποίο
, στο οποίο  . Οι διαγώνιοι του τέμνονται στο σημείο
. Οι διαγώνιοι του τέμνονται στο σημείο  . Η ευθεία
. Η ευθεία  τέμνει τα τμήματα
τέμνει τα τμήματα  και
και 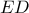 στα σημεία
στα σημεία  και
και  αντίστοιχα. Είναι γνωστό, ότι
αντίστοιχα. Είναι γνωστό, ότι  και
και  . Να αποδείξετε, ότι το μήκος του τμήματος
. Να αποδείξετε, ότι το μήκος του τμήματος  ισούται με την διάμετρο του περιγεγραμμένου στο τρίγωνο
ισούται με την διάμετρο του περιγεγραμμένου στο τρίγωνο  κύκλου. (Α. Κουζνέτσοβ, Ι. Φρόλοβ)
κύκλου. (Α. Κουζνέτσοβ, Ι. Φρόλοβ)

 είναι κοινό μέσο των
είναι κοινό μέσο των και το
και το  κοινό μέσο των
κοινό μέσο των

 είναι παράλληλα και επειδή
είναι παράλληλα και επειδή 
 των αντίστοιχων περιγεγραμμένων κύκλων στα τρίγωνα
των αντίστοιχων περιγεγραμμένων κύκλων στα τρίγωνα 
