Θέματα της πρώτης μέρας για την 11η τάξη.
1. Στον χώρο βρίσκεται ένας άπειρος κύλινδρος ( δηλαδή ο γεωμετρικός τόπος των σημείων, που απέχουν σταθερή απόσταση
από δοθείσα ευθεία 
). Μπορούν άραγε έξι ευθείες, φορείς των ακμών ενός τετράεδρου, να έχουν ακριβώς από ένα κοινό σημείο με αυτόν τον κύλινδρο; (Α. Κουζνέτσοβ)2. Μια τριάδα θετικών αριθμών
θα την ονομάσουμε αινιγματική, αν 
.Να αποδείξετε, ότι αν η τριάδα
είναι αινιγματική, τότε και η τριάδα 
θα είναι αινιγματική. (Α. Κουζνέτσοβ, Κ. Σούχοβ)3. Ο Γιούρι αντίκρυσε την μεγάλη πινακίδα των μάγια, στην πινακίδα υπάρχουν
στήλες και 
γραμμές. Ο Γιούρι ξέρει, ότι σε κάθε κελί της πινακίδας απεικονίζεται ο ήλιος ή το φεγγάρι και οποιεσδήποτε δυο γραμμές διαφέρουν (τουλάχιστον σε μια στήλη). Κάθε κελί της πινακίδας είναι καλυμμένο με ένα φύλλο. Σηκώθηκε ένα αεράκι και φύσηξε μερικά φύλλα: δυο φύλλα σε κάθε γραμμή. Μπορεί άραγε να συμβεί έτσι, ώστε τώρα ο Γιούρι για τουλάχιστον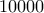 
γραμμές να μπορέσει να μάθει, τι απεικονίζεται σε αυτές σε κάθε στήλη; (Ι. Μπογκντάνοβ, Κ. Κνόπ)4. Το τετράπλευρο
στο οποίο δεν υπάρχουν παράλληλες πλευρές είναι εγγεγραμμένο σε κύκλο 
. Από την κορυφή 
φέρουμε ευθεία 
, από την κορυφή 
φέρουμε ευθεία 
, από την κορυφή 
φέρουμε ευθεία 
, από την κορυφή 
φέρουμε ευθεία 
. Το τετράπλευρο, οι διαδοχικές πλευρές του οποίου βρίσκονται σε αυτές τις τέσσερεις ευθείες (με αυτή την διάταξη), είναι εγγεγραμμένο σε κύκλο 
. Οι κύκλοι και τέμνονται στα σημεία 
και 
. Να αποδείξετε ότι οι ευθείες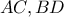 
και 
τέμνονται στο ίδιο σημείο. (Α. Κουζνέτσοβ)
είναι αινιγματική αν και μόνο αν 
και το ζητούμενο έπεται.