 και
και 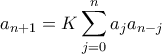 με
με  , ας βρεθεί ο γενικός όρος της
, ας βρεθεί ο γενικός όρος της  .
.Συντονιστής: Demetres
 και
και 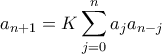 με
με  , ας βρεθεί ο γενικός όρος της
, ας βρεθεί ο γενικός όρος της  .
. η ακολουθία μας και
η ακολουθία μας και  η γεννήτρια συνάρτηση αυτής για όλα τα
η γεννήτρια συνάρτηση αυτής για όλα τα  που συγκλίνει. Tότε παρατηρούμε ότι
που συγκλίνει. Tότε παρατηρούμε ότι  .Θα δουλέψουμε για
.Θα δουλέψουμε για  .
. .Έτσι από την ζητούμενη συνθήκη:
.Έτσι από την ζητούμενη συνθήκη:  .
. .Άρα
.Άρα  .Έτσι έχουμε
.Έτσι έχουμε  . Έτσι θα προκύψει ότι
. Έτσι θα προκύψει ότι  .Έστω ότι
.Έστω ότι  .Γνωρίζουμε ότι
.Γνωρίζουμε ότι  .
.
 .
.  .
. απορίπτεται αφού στο ανάπτυγμα της κοντά στο
απορίπτεται αφού στο ανάπτυγμα της κοντά στο  προκύπτουν και αρνητικοί όροι πράγμα αδύνατο αφού η ακολουθία μας αποτελείται μόνο από θετικούς όρους.
προκύπτουν και αρνητικοί όροι πράγμα αδύνατο αφού η ακολουθία μας αποτελείται μόνο από θετικούς όρους. και η γεννήτρια αυτής η
και η γεννήτρια αυτής η 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες