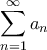 συγκλίνει. Να εξεταστεί αν τα ακόλουθα αθροίσματα συγκλίνουν επίσης
συγκλίνει. Να εξεταστεί αν τα ακόλουθα αθροίσματα συγκλίνουν επίσης(α)

(β)

Συντονιστής: Demetres
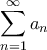 συγκλίνει. Να εξεταστεί αν τα ακόλουθα αθροίσματα συγκλίνουν επίσης
συγκλίνει. Να εξεταστεί αν τα ακόλουθα αθροίσματα συγκλίνουν επίσης

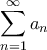 συγκλίνει στο
συγκλίνει στο  αλλά αυτό δεν ισχύει για την σειρά στο (α). Τότε χωρίς βλάβη της γενικότητας θα υπάρχει
αλλά αυτό δεν ισχύει για την σειρά στο (α). Τότε χωρίς βλάβη της γενικότητας θα υπάρχει  ,
,  αρκετά μεγάλο και
αρκετά μεγάλο και  ώστε
ώστε  για κάθε
για κάθε  .
.

 θέτουμε
θέτουμε  αν
αν  περιττός και
περιττός και  αν
αν  άρτιος. Τότε η
άρτιος. Τότε η 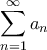 συγκλίνει αλλά (για
συγκλίνει αλλά (για  ).
). της δοσμένης αναδιάταξης ισούται με
της δοσμένης αναδιάταξης ισούται με 
 της δοσμένης αναδιάταξης ισούται με
της δοσμένης αναδιάταξης ισούται με 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 13 επισκέπτες