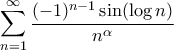 συγκλίνει αν και μόνο αν
συγκλίνει αν και μόνο αν 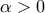 .
.Συντονιστής: Demetres
 ακολουθία φραγμένης κύμανσης (δηλ.
ακολουθία φραγμένης κύμανσης (δηλ. 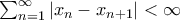 ) με
) με 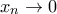 . Τότε, η σειρά
. Τότε, η σειρά 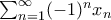 συγκλίνει.
συγκλίνει.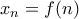 , όπου
, όπου 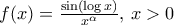 . Εύκολα βλέπουμε ότι
. Εύκολα βλέπουμε ότι 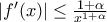 για κάθε
για κάθε  , άρα από το θεώρημα μέσης τιμής έπεται ότι
, άρα από το θεώρημα μέσης τιμής έπεται ότι 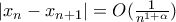 , γεγονός που αποδεικνύει ότι η
, γεγονός που αποδεικνύει ότι η  είναι φραγμένης κύμανσης. Προφανώς,
είναι φραγμένης κύμανσης. Προφανώς, 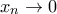 , άρα από το λήμμα έπεται η σύγκλιση της σειράς για κάθε
, άρα από το λήμμα έπεται η σύγκλιση της σειράς για κάθε  .
.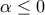 τότε, για την ακολουθία φυσικών αριθμών
τότε, για την ακολουθία φυσικών αριθμών 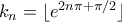 , έπεται ότι ο γενικός όρος δεν πάει στο μηδέν:
, έπεται ότι ο γενικός όρος δεν πάει στο μηδέν: 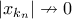 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες