Έστω
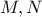
 μιγαδικοί πίνακες με
μιγαδικοί πίνακες με  και
και  . Να δειχθεί ότι υπάρχει αντιστρέψιμος μιγαδικός πίνακας
. Να δειχθεί ότι υπάρχει αντιστρέψιμος μιγαδικός πίνακας  ώστε
ώστε  και
και 
Συντονιστής: Demetres
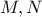
 μιγαδικοί πίνακες με
μιγαδικοί πίνακες με  και
και  . Να δειχθεί ότι υπάρχει αντιστρέψιμος μιγαδικός πίνακας
. Να δειχθεί ότι υπάρχει αντιστρέψιμος μιγαδικός πίνακας  ώστε
ώστε  και
και 
 και
και  . Άρα ο
. Άρα ο  διαγωνοποιείται και έχει ιδιοτιμές
διαγωνοποιείται και έχει ιδιοτιμές  και
και  . Αν
. Αν  είναι μη τετριμμένο ιδιοδιάνυσμα του
είναι μη τετριμμένο ιδιοδιάνυσμα του  στην ιδιοτιμή
στην ιδιοτιμή  , τότε
, τότε  είναι βάση του
είναι βάση του  διότι προφανώς δεν γίνεται
διότι προφανώς δεν γίνεται  (αλλιώς θα ήταν και
(αλλιώς θα ήταν και  ) ενώ αν
) ενώ αν  με
με  ο
ο  θα είχε μη μηδενική ιδιοτιμή (άτοπο). Στη βάση των
θα είχε μη μηδενική ιδιοτιμή (άτοπο). Στη βάση των  οι πίνακες έχουν τις ζητούμενες μορφές διότι
οι πίνακες έχουν τις ζητούμενες μορφές διότι  .
. το χρησιμοποιούμε και σαν στοιχείο του
το χρησιμοποιούμε και σαν στοιχείο του  και σαν πίνακα.
και σαν πίνακα. τότε υπάρχουν
τότε υπάρχουν  ώστε
ώστε  και
και  . Ομοίως υπάρχουν
. Ομοίως υπάρχουν  ώστε
ώστε  και
και  .
. ένας μιγαδικός αριθμός ώστε
ένας μιγαδικός αριθμός ώστε  . Έστω επίσης
. Έστω επίσης  μιγαδικός ώστε
μιγαδικός ώστε  . Τότε
. Τότε  και αλλάζοντας το
και αλλάζοντας το  σε
σε  αν χρειαστεί μπορώ να υποθέσω ότι
αν χρειαστεί μπορώ να υποθέσω ότι  . Ομοίως επιλέγω
. Ομοίως επιλέγω  ώστε
ώστε  .
.  δίνει
δίνει  από το οποίο μετά από πράξεις παίρνουμε
από το οποίο μετά από πράξεις παίρνουμε  . Θέτω λοιπόν
. Θέτω λοιπόν  ή
ή  ανάλογα με το πρόσημο του
ανάλογα με το πρόσημο του  . Ο
. Ο  είναι αντιστρέψιμος και μετά από πράξεις βλέπουμε ότι ικανοποιεί τις ζητούμενες συνθήκες.
είναι αντιστρέψιμος και μετά από πράξεις βλέπουμε ότι ικανοποιεί τις ζητούμενες συνθήκες. βρέθηκε αφού πρώτα ξεκινήσαμε από την μορφή
βρέθηκε αφού πρώτα ξεκινήσαμε από την μορφή  με
με  και μετά είδαμε τι συνθήκες χρειάζονται.]
και μετά είδαμε τι συνθήκες χρειάζονται.]Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες